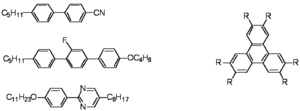Classification and Examples of Liquid Crystals
| Previous Topic | Return to Liquid Crystal Menu | Next Topic |
Liquid crystals can be classified by their behavior and by their physical structure.
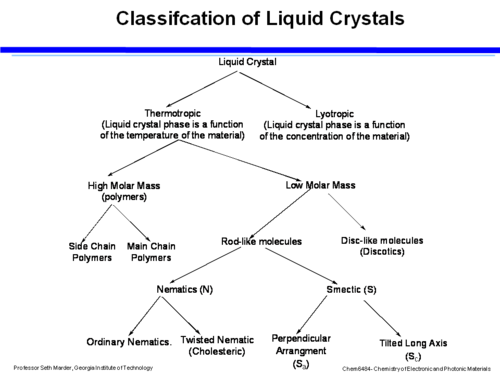
Classification of Liquid Crystals
Liquid crystals can be first organized into thermotropic (temperature dependent) and lyotropic (concentration dependent). Within thermotropic liquid crystals there are high molar mass materials (suitable for polymer) and low molar mass materials. Within the polymeric kind there are main chain polymers where the chains align in a direction, or a chain where there is comb-like structure with side chains that hang off the polymer. The director is oriented either along the main chain or parallel to the side chains.
In the low molar mass materials there are disc like molecules (discotic) and rod like molecules (calamitic liquid crystals). Within the rod-like LC are nematic (N) with ordinary Nematics or Twisted Nematics in which the director changes across the material, and smectic (S) (also known as bookshelf liquid crystals) which tend to line up perpendicularly (Sa) or tilted on the long axis (Sc)
Calamitic vs Discotic
Remember molecules are not liquid crystals--phases are!
The cyanobiphenyls are used routinely in displays. These calamitic liquid crystals have a rigid polarizable core and have a flexible aliphatic tail on one of the sides. The cores makes them want to line up and be more crystalline, while the flexible tail lowers the degree of order so they can flow. The may have polar groups such the cyano group along the main axis, a fluorine group off the main axis, or a dipole moment due to nitrogens in one of the rings along the axis. This will be important when we attempt to orient the materials in an applied field.
The discotics such as triphenylenes can stack up but have long tails (akyl or alkoxy with C12 groups) that allow the discs to remain flexible so they do not become fully crystalline but has a discotic liquid crystal phase.
Calamitic Liquid Crystals
Nematic Liquid Crystals
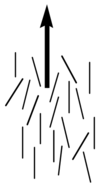
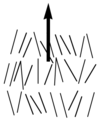
Nematics (from the Greek: nematon- thread-like) are uniaxial liquid crystals in which the average direction of the long axes of the molecules defines the direction N.
Nematic liquid crystals have one axis in which the polarizability, and the dielectric constant and the index of refraction are different from the other two axes (the illustration is exaggerated for how aligned the molecules would be) Note the lack of positional order along the axis of the director. The spacing between molecules in all directions is not uniform. They have characteristic textures when viewed under cross polarized light microscope. These materials are birefringent and allowing light with different polarizations to go through at different speeds.
Two examples are cyanobiphenyls and another with rigid and mantle group in the system.
It is important to be able to control the temperature range in which liquid crystals operate. Most liquid displays are not made up out of single molecules. It is made up with a combination of molecules that gives the desirable transition temperatures on the low end and high end of operating temperatures.
For more liquid crystal images see Liquid Crystal Institute
Cholesteric Phase
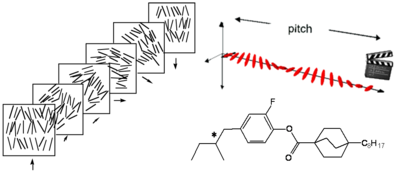
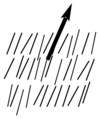
Cholesteric is the nematic state superimposed with a natural twist between layers including the long axis of the molecules induced by the incorporation of chiral group to give helical twist to the orientation of the director.
The pitch is the period for the director to rotate 180 degrees. The pitch of the twist is quite sensitive to temperature.
Adding a chiral dopant to a nematic liquid crystal will induce a helical twist to create a chiral nematic phase. Remember it is the phase that is chiral not necessarily the molecule itself.
A cholesteric liquid can diffract light differently depending upon the pitch of the liquid crystal according to the equation λ = np, where λ is the wavelength of light, n is the refractive index and p is the pitch. Because of the periodic pitch there is a lattice spacing and therefore it is possible to diffract light. This accounts for the colors often seen.
The pitch is very sensitive to temperature and accordingly, cholesteric LC have temperature dependent optical properties--remember mood rings
Smectic Phases
Smectic phases have more positional order perpendicular to the director resulting in a “bookshelf “ordering.
Smectic A is a phase in which the molecules are parallel to one another and are arranged in layers with the long axes perpendicular to the layer plane. This gives rise characteristic textures.
Smectic C is a smectic A like structure in which the long axes of the molecules of a tilted average angle differing from 90° with respect to the plane of the layer in a "bookshelf” arrangement. Light can be diffracted off the periodic spaces give a variety of patterns.
This molecule goes from crystalline to Smectic B, to smectic, C to smectic, A to nematic, to isotropic at various temperatures.
- <math>K \quad _{\overrightarrow {113^{\circ} C}} \quad B \quad _{\overrightarrow {144^{\circ} C}} \quad C \quad _{\overrightarrow {172^{\circ} C}} \quad A \quad _{\overrightarrow {200^{\circ} C}} \quad N \quad _{\overrightarrow {200^{\circ} C}} \quad I\,\!</math>
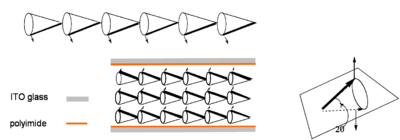
Smectic C* If a smectic phase is chiral and has an off axis dipole then as you go from layer to layer the director will maintain a tilt angle with respect to the layer plane but that rotates about a cone from layer to layer. The molecules can rotate about the cone; a chiral rotation. Smectic C* often have a dipole that off the axis of the director.
For more liquid crystal images see Liquid Crystal Institute
Ferroelectric Smectic C*
If the helix can be unwound such that all the dipoles (and directors stay at the same angle as shown below) then the molecules will form a ferroelectric phase. The bulk material will have a net alignment of all the dipoles and therefore a bulk dipole moment. Unwinding is accomplished by use of a surface stabilizing layer and on both ends of a cell whose length a shorter than the helical pitch and the materials is thus called a surface stabilized ferroelectric LCD (SSFLCD). The cell is coated with a polyimide and unidirectionally rubbed, causing the molecular layers near the surface to align with the direction of rubbing. This results in a bulk electric field in the material due the alignment of all the dipoles. This means that the change in the field can cause the dipoles to rotate which changes the orientation of the director which in turn influences the optical properties of the material.
This was pioneered by Noel Clark at UC Boulder [1]
Discotic Liquid Crystals
A discotic phase in one is which flat molecules typically with threefold or four fold symmetry that have a rigid core and several floppy side chains stacked with their planes lying roughly parallel to one another. Thus, the director is oriented roughly perpendicular to the plane of the molecule. If you throw pieces of paper down they will stack up as parallel planes. There is a difference in the definition of the director between calamitic and nematic liquid crystals. In calamitic liquid crystals the director is defined as being along the axis of the moment of inertia of the molecules. In nematic liquid crystals the director is perpendicular to the average plane of all the liquid crystals.
In nematic discotics phases there is no positional order between the molecules, only orientational order.
In the case of columnar discotic phases the molecules themselves lie roughly on top of each other, so there is some degree of positional order. This columns of discs tend to form hexagonal patterns and these phases are called hexagonal columnar discotics. Columnar molecules can have specific shapes which cause them to line up perfectly or rotate as they fit together.
Klaus Mullen is a talented chemist at the Max Planck Institute for Polmer Science in Mainz. He has started to make graphitic type molecules based on molecules such as triphenylene, thalocyanine, and hexobenzochoridine. The common characteristic is a common π core that is roughly flat with flexible alkyl chains on the periphery. These molecules have been examined for use as charge transport materials.
see Mullen 2004 [2]
Charge Transport in Liquid Crystals
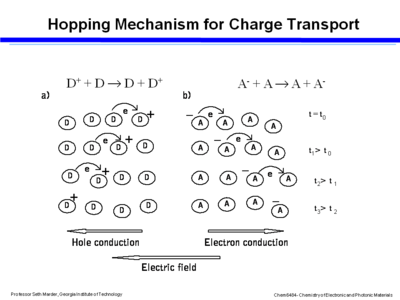
Hopping Mechanism for Charge Transport
In the hopping model of transport there is series of redox reactions in which electrons are transferred from site to site. This requires a good overlap between the orbitals. Discotic crystals have the ability to overlap.
See Band Regime versus Hopping Regime
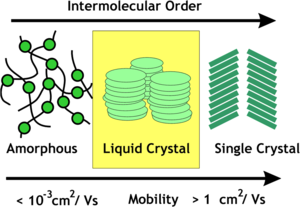
Increasing Order in Materials
The charge mobility increases with the increase in intermolecular order. An amorphous polymer has no crystalline order, no positional order or orientational order. At the other extreme is the crystalline order that is “perfectly” stacked. Usually even crystals that are 99.9% pure will have an impurity in a cell that is only 10x10x10 molecules. Cyrstals are seldom pure or perfect. The typical tools we use for elemental analysis have an error bar in the range of impurity concentrations that will cause a problem for electronic purposes. Elemental analysis can tell you things are not good, but can’t really tell you that you are dealing with pure materials.
There is an intermediate a degree of order in the liquid crystal materials. Both discotic and calamitic materials have been explored for transport. The predictability of getting a discotic liquid crystalline phase is somewhat higher that predicting crystal structures. However, the degree of certainty of where the molecules are in the liquid crystal phase is lower that you get with a single crystal that can be studied with a X-ray crystallography.
Charge mobilities (measured in cm2/Vs) for amorphous materials are <10-3 and single crystal are more than 1 cm2/Vs (typical of amorphous silicon)
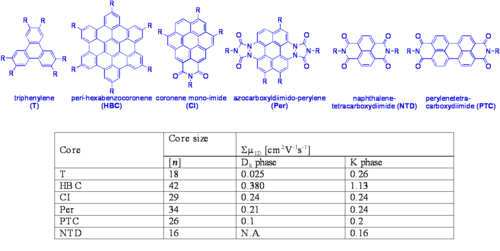
Core Size Effects on Charge Mobility
This study shows that for a certain class of the molecules with increasing core size there is a tendency for higher mobilities. There may be specific interactions that lead to a higher degree of order and there molecular properties which contribute to higher mobility. All these discotic liquid crystal materials have better mobilities than amorphous materials.
See Warman 2001 [3].
Extending the size of the core: From Perylene to Coronene
The perylene diimide has a columnar discotic pattern with a mobility of about 1 cm2/Vs . A coronene with a large core with a mobility of 3 cm2/Vs. You can use these materials for their electronic properties as well as their optical properties.
Summary of Phases and Order
| phase | order |
|---|---|
| Isotropic liquid | full continuous translational and rotational symmetry (on average) |
| Nematic | molecular orientation breaks rotational symmetry, one axis is different from another axis |
| untilted | tilted |
|---|---|
| Smectic-A | Smectic-C layering breaks translational symmetry; in smectic-C molecules are tilted |
| Hexatic SBSI SK | Like the smectic A they are stacks of liquid layers but the molecules tend to be positioned along a hexagonal lattice within each plane |
Plastic crystals - Smectic (Crystal) - B the rigid part of the crystals stay ordered but the long chain aliphatic tail melt (according to de Gennes), more appropriately called a crystal
Crystal- molecular rotation freezes out
- The degree of order increases from the top to the bottom of the table. In general, phases from the top of the table are expected at high temperatures, and phases from the bottom at low temperatures.
- In the discotic phase, and columnar phases, translational symmetry is broken in not one but two spatial directions, leaving liquid-like order only along columns.
References
- ↑ N.A. Clark and S.T. Lagerwall, Appl. Phys. Lett., 1980, 36, 899
- ↑ http://www.rsc.org/ej/jm/2004/b312789c.pdf
- ↑ van de Craats, A. M.; Warman, J. M. Adv. Mater. 2001, 13,130-133
| Previous Topic | Return to Liquid Crystal Menu | Next Topic |