Terahertz Radiation

Previous Topic

Return to Second-order Processes, Materials & Characterization Menu

Next Topic

Error creating thumbnail: File with dimensions greater than 12.5 MP

1 THz ~ 300 µm wavelength ~33 wave numbers ~ 4 meV- Courtesy of www.SURA.org

Terahertz (THz) is Far-Infrared radiation located between microwaves and infrared in the electromagnetic spectrum. It is low-energy, non-ionizing radiation which can penetrate many non-polar, non-conducting materials such as clothing, paper, masonry or plastic. Possible applications of THz include:

• Medical imaging - THz can penetrate several millimeters into tissues with low water content, or deep into teeth, without damage. For example: THz can be used for burn depth assessment, skin cancer identification, etc.
• Security screening- THz can penetrate clothing and reveal hidden weapons. Explosives, biological agents, and controlled substances have specific spectral signatures allowing for chemical identification.
• Spectroscopy- THz time domain spectroscopy can measure the low-energy, far-infrared properties of substances that are opaque in the visible and near-infrared regions of the spectrum. In particular, collective vibrations, phonon resonances, and scattering rates of charge carriers are typically in the THz range.
• Manufacturing- Circuit boards, device components, and the contents of paper packages can be easily visualized for quality control. For example, THz inspections can identify voids in space shuttle foam, like those responsible for the Columbia disaster.

History of THz Science

A THz-TDS/OPTP experimental setup

Far-infrared studies have occurred since the invention of the bolometer in 1881 by astronomer Samuel Langley. Much of the early far-infrared work was done by Rubens, who discovered reststrahlen sources enabling measurements crucial to Planck's blackbody radiation theory. Far-infrared transmission studies of superconductors confirmed the energy gap predicted by Bardeen, Cooper, and Schrieffer's superconductivity theory. Since the invention of frequency-division multiplexing in 1949, Fourier-transform infrared spectroscopy became a standard tool in physical chemistry. Over the years, numerous sources and detectors have been discovered e.g. Golay cell, water-vapor laser, pyroelectric detector, synchrotrons, free-electron lasers, and quantum cascade lasers.

Modern pulsed-THz sources grew out of the work of Auston, Nuss, and Grischkowsky on photoconductive switches, electrical pulses on transmission lines, and far-infrared emission from nonlinear crystals in the 1980s. Since their pioneering work, photoconductive switches have become one of two popular methods of generation and coherent detection of bright THz pulses with high sensitivity. The other popular modern method involves generation of broadband THz radiation via "optical rectification" and coherent detection of the THz waveform through free-space electro-optic sampling, both occurring in nonlinear optical media.

THz generation and detection

THz radiation is typically generated via optical rectification (OR), of laser pulses from a single source, in a nonlinear optical (NLO) material or impulsively from photoconductive dipole antennae (PDA). Difference-frequency generation (DFG) between two different laser beams in a NLO material can also be used to generate THz radiation. PDAs can also be used to coherently detect the THz waveform, through the detected photocurrent. Second order NLO materials can be coherent detect THz pulses through the free-space electro-optic sampling (FSEOS).

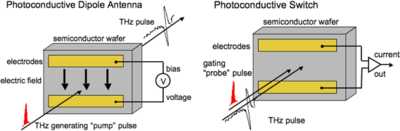
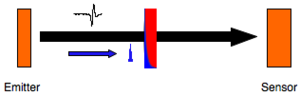
Photoconductive Dipole Antennae

Schematic of photoconductive dipole antenna emitter and sensor

In a PDA, THz radiation is emitted by an ultra-fast transient photo-current created in a biased semiconductor, typically GaAs. The semiconductor is photo-excited with an ultra-short pulse to generate short-lived charges, which are accelerated with an applied electric field. The emitted field, <math>E_{THz}</math> is related to the current, J, by

<math>E_{THz}\propto\partial J/\partial t</math>

Though PDAs are bright THz sources, finite carrier lifetimes limit the bandwidth available from photoconductive materials to less than that achievable via OR in NLO materials. Detection of the THz pulse occurs, essentially, through the opposite effect. An ultra-short pulse generates short-lived charge carriers, which are subsequently accelerated by the THz electric field. This generates a transient current between two electrodes, which is proportional to the amplitude and direction of the THz electric field making this a coherent detection technique. A delay stage allows for the one pulse to be moved in time with respect to the other, similar to a correlation, such that the THz waveform is sampled point-by-point by the "probe" pulse

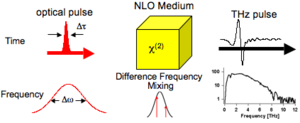
Optical Rectification in a Nonlinear Optical Medium

THz "Optical-rectification" generates broadband THz pulses via difference frequency mixing of the frequency components of an ultra-short pulse

OR is more properly though of as difference frequency mixing. In a NLO material, the polarization induced by an AC electric field will not reverse its sign at the same time as the driving field, leading to a nonlinear polarization and thus frequency mixing. If the field is applied with a femtosecond laser pulse, with a large spectral bandwidth, difference frequency mixing of different frequency components results in electromagnetic waves in the terahertz region. This is the optical analog of the audible beat frequency generated by two struck tuning forks. The emitted field is related to the polarization, P, by

<math>E_{THz}\propto\partial^{2} P/\partial t^{2}</math>

The efficiency of THz generation depends on the second order nonlinear susceptibility of the medium. Popular materials include: inorganic NLO crystals (e.g. ZnTe, GaP), organic NLO crystals (e.g. DAST), NLO guest-host electro-optic (EO) polymers. See Sum and Difference Frequency Generation

Free-Space Electro-Optic Sampling

Free-space electro-optic sampling experimental schematic

In free-space electro-optic sampling (FSEOS), the THz waveform and a ultra-short "probe" pulse propagate collinearly through an EO medium. In the absence of the THz pulse, the "probe" pulse has a linear polarization that it changed to be circular by the compensator and is separated into s- and p- components by the Wollaston polarizing beam splitter. For equal s- & p- components, the balanced photodiodes produce null current. In the presence of the THz field, the EO medium becomes birefringent through the Pockel effect, and the polarization of the probe is rotated. The imbalance in s- and p- polarization causes a current, proportional to the THz field and direction, to flow from the balanced photodoides. Again, a delay stage allows for the one pulse to be moved in time with respect to the other, such that the THz waveform is sampled by the "probe" pulse. The detected current, <math>I_{det}</math> is related to the optical index, n, effective EO coefficient, <math>r_{eff}</math>, and sensor thickness, d by

<math>I_{det}\propto n^{3}r_{eff} d E_{THz}</math>

As the recorded current is proportional to the time-dependent THz electric field, this is also a coherent detection technique. See Electro-optic effects

EO Polymers for THz

Poor phase matching due to a 5.3 THz phonon limits the bandwidth available using the inorganic crystal ZnTe as a THz sensor. Improved phase matching and a coherence length of 50 <math>\mu</math>m at 10 THz allows for broadband THz detection in this EO polymer

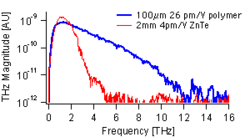
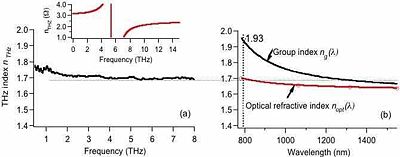
EO poled guest-host polymers have the potential to achieve orders of magnitude higher optical nonlinearities than crystalline materials. Poled polymers have achieved electro-optic coefficients >400 pm/V, which is two orders of magnitude larger than the inorganic crystal ZnTe, a standard material for THz generation and detection. The tunable optical and NLO properties of poled polymers, along with good phase matching, makes them valuable for THz applications. For example, poled polymers have been used to achieve a broad bandwidth THz system at telecommunications wavelengths, where compact laser systems are available. Due to their relatively flat THz index of refraction, proper choice of the "pump" wavelength would allow for phase matching across the THz band even for very thick polymers.

See Poling Polymers Basics

Phase (velocity) matching by comparing the THz (a) and the visible (b) indices of refraction of EO poled polymers. The Lorentz Oscillator model of the THz index of ZnTe is included in the inset of (a) for reference.

Phase matching (i.e. velocity matching) is necessary for efficient THz generation and detection. For efficient energy transfer between the optical and THz pulses, they should travel through the NLO medium at the same velocity. The distance over which the THz and optical travel in phase is the coherence length, <math>l_{c}</math>,

<math>l_{c}=\frac{\pi c}{\omega\left|n_{grp}-n_{THz}\right|}</math> <math>n_{grp}=n_{opt}-\lambda_{opt}\partial n_{opt}/\partial\lambda_{opt}</math>

where c is the speed of light, <math>\omega = 2 \pi f</math>, f is the THz frequency, <math>\lambda_{opt}</math> is the "pump" wavelength, and <math>n_{opt}</math> and <math>n_{THz}</math> are the optical and THz indices of refraction of the NLO medium. For thicker emitters, destructive interference occurs between newly generated THz pulses and those generated earlier in the material, reducing the amplitude at the mismatched frequencies. Due to phonon lattice resonances in the THz regime, NLO crystals can be quite dispersive across this band. Many crystals are also disperive in the visible and near infrared (NIR). Polymers have very low dispersion. Their NIR and THz indices of refraction are nearly the same, yielding very good phase matching and allowing for broadband THz generation.

Spectroscopy Applications

THz time-domain spectrometer experimental schematic

THz radiation is commonly used for spectroscopic applications to elucidate the far-infrared properties of a variety of material systems. THz is used for variety of spectroscopic techniques e.g. transmission and reflection mode time-domain spectroscopy, optical-pump THz-probe spectroscopy, attenuated total reflectance, near-field scanning optical microscopy, etc.

The appeal of THz for spectroscopy is mainly:

• coherent detection provides access to the electric field and thus the determination of the complex dielectric properties without the need for Kramers-Kronig analysis
• the low energy radiation has good penetration through non-conductive, non-polar materials
• low frequency oscillations correspond to phonon modes, molecular vibrations, and other collective oscillations which are unique to many materials and dynamic processes
• carrier scattering rates typically lay between 1-100 THz, providing useful information on charge carrier transport in conductive and photoconductive materials

see e.g. "THz Spectroscopy: Principals and Applications," Edited by S. Dexheimer, CRC press (2008)

THz Time Domain Spectroscopy

In THz Time Domain Spectroscopy, a ~1ps single-cycle THz pulse is propagated through a sample.

Optical-Pump THz Probe Spectroscopy

In THz-TDS, the transmission of the THz waveform (electric field) through a sample is measured and compared to a reference, typically the transmission through the experiment without a sample present. Modeling normal incidence transmission through the sample with Fresnel coefficients, and assuming <math>\kappa << n</math>, the index of refraction, n, and the power absorption coefficient <math>\alpha</math> are

<math>n(\nu)\approx1+\frac{c}{d\omega}\left|\Delta\Phi \right|</math> <math>\alpha(\nu)\approx-\frac{2}{d}ln\left(\frac{1}{T}\frac{Mag_{sample}}{Mag_{ref}} \right)</math>

where <math>\omega = 2\pi\nu</math>, <math>\alpha =\omega \kappa / 2 c</math>, d is the sample thickness, c is the speed of light, T are the Fresnel transmission coefficients to correct for reflective losses, <math>\Delta\Phi</math> is the measured change in THz phase, and <math>Mag_{sample}</math> is the magnitude of the THz transmission through the sample.

The index of refraction of amorphous polycarbonate from 0-7THz.

The extracted index of refraction and absorption can be of interest for a number of reasons. Typically, its frequency dependence can be modeled to extract information about the underlying physics. If the material is of interest to THz optics, knowledge of its optical properties are vital. For example, knowledge of the THz index of refraction of a material of interest for THz emission and detection is needed to determine phase matching conditions. The complex dielectric function can also be computed from the index of refraction and absorption coefficient. If the material is conducting, the complex conductivity can also be computed. This allows for conductivity models to be applied to model the frequency dependence and describe the underlying charge carrier motion.

Optical Pump THz Probe Spectroscopy

In Optical-Pump THz-Probe Spectroscopy, a THz pulse is propagated through a photo-excited sample.

In Optical-Pump THz-Probe Spectroscopy (OPTP), a.k.a. time-resolve THz spectroscopy, the THz waveform transmitted through a photo-excited sample is compared to that transmitted through the unexcited sample. Through fourier analysis, the full frequency dependent complex conductivity can be obtained. Modeling on this photo-induced conductivity, e.g. with the Drude model or a variation there of, yields the mobility and carrier density, also giving the photon-to-carrier yield. Control of the delay between the optical photo-excitation pulse (the "pump") and the THz pulse (the "probe") allows us to map out the time evolution of the photoexcited state.

The appeal of THz for spectroscopy is mainly:

• Non-contact, low energy (meV), non-perturbing, optical probe with sub-ps resolution
• Direct access to the complex conductivity of the material system under study
• Sensitive to (free) charge carrier scattering (i.e. damping) rate, and low-frequency oscillation of bound-charges (e.g excitons)

Modes of Operation

Error creating thumbnail: Unable to save thumbnail to destination

(left) Photoconductivity dynamics described by pump-delay dependent changes in THz transmission through the photoexcited sample. (Right) The change in the transmitted THz waveform is recorded at various delays to allow for the extraction of the evolving frequency-dependent dielectric properties.

OPTP experiments can be operated, essentially, in two ways. The first, involves monitoring changes in a single point on the THz waveform as the "pump" delay stage is moved. Typically referred to as a "pump" scan, this mode allows for the average excited state dynamics to be mapped out with respect to the delay after the photo-excitation event. The other, involves recording the entire THz waveform transmitted through an excited sample at various delays after excitation. Typically referred to as a "probe" scan, this mode allows us to map the evolution of the frequency-dependent dielectric properties of the excited state.

To extract the complex conductivity, a variety of models and techniques can be used, we use the following approximate analytic relationship

<math>\tilde{\sigma} (\omega) \approx - \frac {(n_{THz} +1 )}{Z_0d}\frac {\Delta \tilde{E}(\omega)}{\tilde{E}_0(\omega)}\,\!</math>

where<math>d\,\!</math> is the absorption depth at λ_exc. Once the complex conductivity is extracted from the raw data, a variety of conductivity models, e.g. Drude, Cole-Cole, Cole-Davidson, Lorentz-Oscillator, Localized-Drude, Drude-Smith, etc., can be applied to model the excited state dynamics. In the case of charge carrier motion, where Drude-like models are typically used, this leads to estimation of the carrier scattering time, i.e. mobility, and carrier density, i.e. photon-to-carrier yield. In the case of an excitonic response, the bound charge oscillation can be modeled to estimate the exciton polarizability and binding energy.

see F. A. Hegmanne.

Examples in Materials Science

THz-TDS and OPTP spectroscopy have been used for a number of materials science studies, from the properties of dielectrics, solvation dynamics, metamaterials, insulator-metal transitions, high-temperature superconductivity, colossal magnetoresistance, and carrier dynamics in semiconductors, nanostructures, and organics. Below, a cross-section of materials studies examples are listed to illustrate the potential of THz spectroscopy.

Carrier Dynamics

Excitation at 800nm vs 400nm. (Left) A band diagram of GaAs shows that the excess 1.49eV provided by the 400nm excitation allows carriers to scatter to higher valleys. (Right) The longer rise time of the 400nm photo-induced conductivity signal corresponds to the time required for carriers to return to the high mobility gamma valley.

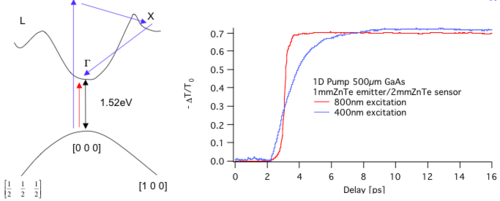
Here, OPTP spectroscopy has be used to examine carrier dynamics in the popular semiconductors semi-insulating GaAs. The onset of conductivity in this material occurs when electrons are in the high-mobility Γ-valley in this direct-gap semiconductor. However, high energy photons can promote electrons with sufficient energy to scatter to satellite X & L-valleys, where the mobility is much lower. The process of these electrons returning to the Γ-valley by phonon emission results in THz absorption by free-electrons.

The conductivity observed in an amorphous polymer at various delays after photo-excitation shows an evolution from dispersive transport to a bound excitonic response..

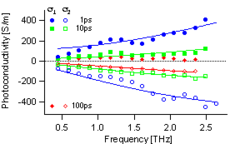
Here, OPTP spectroscopy has been used to examine carrier dynamics in an amorphous semiconducting polymer film. The complex conductivity evolves over time until the real conductivity is nearly zero and the imaginary conductivity is negative and linear with frequency. This signature has come to be associated with bound excitons. At early delays, a variety of conductivity models could describe the dispersive transport seen, including the Drude-Smith model, Debye relaxation, and the Lorentz oscillator model.

Carrier trapping

comparison of the photo- conductivity of low-temperature grown GaAs with semi-insulating GaAs

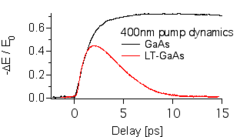
Here, OPTP spectroscopy was used to identify carrier trapping. There is a rapid decrease in THz absorption in photoexcited low-temperature grown GaAs as compared to semi-insulating GaAs. This is caused by a reduced carrier lifetime, as the low-temperature growth results in As clusters, which yield energy levels within the band gap and act as traps.

Electron Transfer

Error creating thumbnail: Unable to save thumbnail to destination

Ultrafast electron transfer from P3HT to PCBM is marked by an increase in the long lived photoconductive state in the bulk heterojunction compared to neat films of P3HT.

Here, the sub-picosecond time resolution was used to study ultrafast electron transfer from regioregular P3HT to the soluble fullerene derivative PCBM. There is a marked increase in THz absorption in the P3HT/PCBM bulk-heterojunction blend as compared to photoexcited films of P3HT alone. The increase in the yield of this long-lived conductive state is due to more efficient charge separation, as it is energetically favorable for electrons to transfer to PCBM and holes to transfer to P3HT, reducing the change of recombination. Ultrafast electron transfer is the principle behind how many organic photovoltaic cells work, in particular, efficient electron transfer and good conductive properties make P3HT/PCBM a standard in the organic solar cell community.

Temperature Dependent Conduction

The imaginary conductivity of the high-temperature superconductor HBCCO shows a sharp increase below the critical temperature due to Cooper pairing

Here, THz TDS was used to study the temperature dependent dielectric properties, i.e. conductivity, of the high-temperature superconductor HBCCO. A marked increase in the imaginary component occurs below the critical temperature, where Cooper pairing becomes efficient. At low temperatures, the conductivity is described by the properties of both superconducting Cooper-pairs and normal state electrons, while at high temperature the conductivity is Drude-like. OPTP can be used to study Cooper-pairing dynamics, as optical excitation breaks apart Cooper-pairs into metastable quasiparticles.

External Links

See Wikipedia Terahertz Radiation

See Wikipedia Terahertz time-domain spectroscopy

See Wapedia Terahertz

See THz Group Wiki- password required THz Polymers Wiki

References

Previous Topic

Return to Second-order Processes, Materials & Characterization Menu

Next Topic