Dispersion and Scattering of Light
| Previous Topic | Return to Basics of Light Menu | Next Topic |
Dispersion
Light can also disperse. The index of refraction depends on the wavelength. We don’t have the capability of sending a perfectly monochromatic light into an optical fiber, therefore there will be some dispersion of light. This also has implications for optical fibers. We must pick materials for optical fibers that do not absorb in the near IR, the popular wavelength for telecommunications. In general terms as the index of refraction increases the wavelength decreases. For example, n for blue light is larger than n for red light. A blue photon has an energy of about 3 eV, vs 1.5 eV on the red side of the spectrum.
Dispersion is defined as
- <math>\frac {dn(\lambda)}{d\lambda}\,\!</math>
If you send white light into a material the material will respond differently to each wavelength of light. Therefore the angle of deflection will be slightly different for each color. This explains how a prism makes a rainbow. White light passes from air into the glass and becomes decomposed into each color.
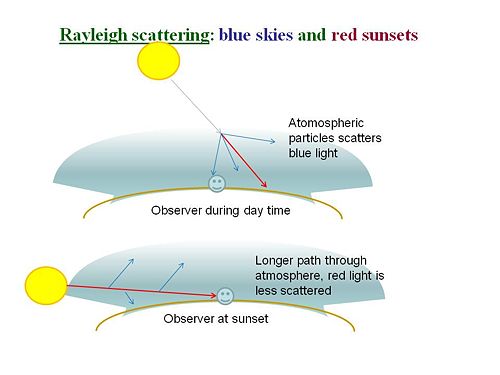
Raleigh Scattering
Plane glass is an amorphous material with no crystalline structure. This prevents various refractive processes from occurring that would ruin its transparency. This is why optical fibers are made with amorphous materials. Light can be scattered in any inhomogeneous medium, that is, if there are fluctuations in the refractive index. Amorphous materials tend to be inhomogeneous.
Here is a light beam I0 that is coming from the left towards a scattering center.
<math>\rightarrow{I_0} \star \rightarrow{\theta}\,\!</math>
The expression for Rayleigh scattering is given by:
- <math>I_s (\theta)\propto I_0 \; \frac{V^2} {\lambda^4} ( 1 + cos^2 \theta)\,\!</math>
where:
- <math>R\,\!</math> is the distance to the particle or scattering center
- <math>\theta\,\!</math> is the scattering angle
- <math>V\,\!</math> is the volume of the scattering particle
It is valid for small spherical scattering particles of volume V with a diameter less than 1/10 of λ of incident light.
The scattering particles (scattering centers) can be as small as a single molecule
Scattering depends on the angle but it is not an all or nothing relationship. The intensity of the beam going straight vs θ at 90 degrees exhibits a factor of 2 difference because of the <math>( 1 + cos^2 \theta)\,\!</math> expression. Otherwise there would be much more effect from the angle.
Since Rayleigh scattering is proportional to <math>\frac{1}{\lambda^4}\,\!</math> scattering is larger for blue light than for red light. For a given angle of scattering the blue light will be scatter 16x as much as the red. This is the reason the sky is blue.
See wikipedia:Rayleigh_scattering
Please note that others may also have edited the contents of this article.
|
| Previous Topic | Return to Basics of Light Menu | Next Topic |