Diffraction of Light
| Previous Topic | Return to Basics of Light Menu | Next Topic |
Diffraction effects occur when waves interact with objects having a size similar to the wavelength of radiation. Diffraction is not important for optical fibers because there must be some specific order in the materials in order to have a diffraction pattern. And optical fibers are deliberately made from amorphous solids or glasses.
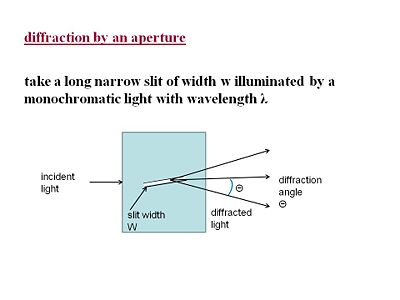
Diffraction through an aperature
When light goes through a slit there are two regimes that have been explored; close to the object as in Fresnel diffraction, and the effects of diffraction far from the object: Fraunhofer diffraction.
The result of diffraction is a set of bright and dark fringes, due to constructive and destructive wave interference, called a diffraction pattern.
The intensity observed far from the slit is given by:
- <math>I = I_0 (\frac {sin\alpha} {\alpha})^2\,\!</math>
where
- <math>\alpha = \pi w \; sin(\frac {\theta}{\lambda})\,\!</math>
minima are found for <math>\theta\,\!</math> values such that:
- <math>sin \theta_{min} = j\;\frac {\lambda} {w}\,\!</math>
with j = ±1, ±2, ±3, …
Therefore: the narrower the slit, the wider the fringe spacing
If white light is diffracted, each λ will be diffracted through a slightly different angle. Red light is diffracted through a wider angle than violet light because sin θ is related to wavelength.
Single Slit interference simulator.
Diffraction Gratings
Planar diffraction gratings consist of an object inscribed with a set of parallel lines which have a spacing similar to that of the wavelength of light.
transmission gratings have alternating clear and opaque lines diffraction effects are seen for light passing through the clear strips.
reflection gratings consist of a set of grooves that are regularly spaced diffraction effects are seen for light reflected from the patterned surface.
The grooves can be formed by photochemical reactions that leads to the displacement of the materials on the surfaces forming grooves. This is interesting because these patterns can be used to store information.
Line spacing
The positions of the diffraction maxima in the case of a transmission grating occur for:
- <math>sin \theta_{max} = n \frac {\lambda} {d }\,\!</math>
with n = ±1, ±2, ±3, …
D is the spacing the lines.
Double Slit interference simulator.
Diffraction by crystals
Atoms in crystals have spacings similar to the λ of x-rays and form a 3-D grating for such light. The diffraction patterns can be used to infer the structure of the molecules in the crystal.
External Links
See wikipedia:Optics
Please note that others may also have edited the contents of this article.
|
| Previous Topic | Return to Basics of Light Menu | Next Topic |