Difference between revisions of "Terahertz Radiation"

From CleanEnergyWIKI
Jump to navigation Jump to search
Line 16: Line 16:


<br clear='all'>
<br clear='all'>
===History of THz Science===
==History of THz Science==
[[Image:Thz_setup.jpg|thumb|300px|A THz-TDS/OPTP experimental setup]]
Far-infrared studies have occurred since the invention of the bolometer in 1881 by astronomer Samuel Langley. Much of the early far-infrared work was done by Rubens, who discovered reststrahlen sources enabling measurements crucial to Planck's blackbody radiation theory. Far-infrared transmission studies of superconductors confirmed the energy gap predicted by Bardeen,Cooper, and Schrieffer's superconductivity theory. Since the invention of frequency-division multiplexing in 1949, Fourier-transform infrared spectroscopy became a standard tool in physical chemistry. Over the years, numerous sources and detectors have been discovered e.g. Golay cell, water-vapor laser, pyroelectric detector, synchrotrons, free-electron lasers, and quantum cascade lasers.
Far-infrared studies have occurred since the invention of the bolometer in 1881 by astronomer Samuel Langley. Much of the early far-infrared work was done by Rubens, who discovered reststrahlen sources enabling measurements crucial to Planck's blackbody radiation theory. Far-infrared transmission studies of superconductors confirmed the energy gap predicted by Bardeen,Cooper, and Schrieffer's superconductivity theory. Since the invention of frequency-division multiplexing in 1949, Fourier-transform infrared spectroscopy became a standard tool in physical chemistry. Over the years, numerous sources and detectors have been discovered e.g. Golay cell, water-vapor laser, pyroelectric detector, synchrotrons, free-electron lasers, and quantum cascade lasers.


Line 23: Line 24:
<br clear='all'>
<br clear='all'>


=== THz generation and detection ===
== THz generation and detection ==
THz radiation is typically generated via optical rectification (OR)  in a nonlinear optical (NLO) material or impulsively from photoconductive dipole antennae (PDA).  
THz radiation is typically generated via optical rectification (OR), of laser pulses from a single source, in a nonlinear optical (NLO) material or impulsively from photoconductive dipole antennae (PDA). Difference-frequency generation (DFG) between two different laser beams in a NLO material can also be used to generate THz radiation. PDAs can also be used to coherently detect the THz waveform, through the detected photocurrent.  Second order NLO materials can be coherent detect THz pulses through the free-space electro-optic sampling (FSEOS).
 
<br clear='all'>
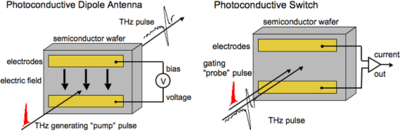
===Photoconductive Dipole Antennae===
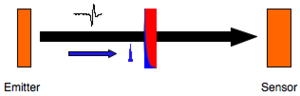
[[Image:THz_PDA.png‎|thumb|400px|Schematic of photoconductive dipole antenna emitter and sensor]]
[[Image:THz_PDA.png‎|thumb|400px|Schematic of photoconductive dipole antenna emitter and sensor]]
In a PDA, THz radiation is emitted by an ultra-fast transient photo-current created in a biased semiconductor, typically GaAs. The semiconductor is photo-excited with an ultra-short pulse to generate short-lived charges, which are accelerated with an applied electric field. The emitted field, <math>E_{THz}</math> is related to the current, <em>J</em>, by
In a PDA, THz radiation is emitted by an ultra-fast transient photo-current created in a biased semiconductor, typically GaAs. The semiconductor is photo-excited with an ultra-short pulse to generate short-lived charges, which are accelerated with an applied electric field. The emitted field, <math>E_{THz}</math> is related to the current, <em>J</em>, by
<center><math>E_{THz}\propto\partial J/\partial t</math></center>
<center><math>E_{THz}\propto\partial J/\partial t</math></center>
Though PDAs are bright THz sources, finite carrier lifetimes limit the bandwidth available from photoconductive materials to less than that acheivable via OR in NLO materials. Detection of the THz pulse occurs, essentially, through the opposite effect.  An ultra-short pulse generates short-lived charge carriers, which are subsequently accelerated by the THz electric field. This generates a transient current between two electrodes, which is proportional to the amplitude and direction of the THz electric field making this a coherent detection technique. A delay stage allows for the one pulse to be moved in time with respect to the other, similar to a correlation, such that the THz waveform is sampled point-by-point by the "probe" pulse
Though PDAs are bright THz sources, finite carrier lifetimes limit the bandwidth available from photoconductive materials to less than that acheivable via OR in NLO materials. Detection of the THz pulse occurs, essentially, through the opposite effect.  An ultra-short pulse generates short-lived charge carriers, which are subsequently accelerated by the THz electric field. This generates a transient current between two electrodes, which is proportional to the amplitude and direction of the THz electric field making this a coherent detection technique. A delay stage allows for the one pulse to be moved in time with respect to the other, similar to a correlation, such that the THz waveform is sampled point-by-point by the "probe" pulse
 
<br clear='all'>
 
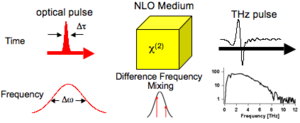
===Optical Rectification in a Nonlinear Optical Medium===
[[Image:THz_OR.png|thumb|300px|THz "Optical-rectification" generates broadband THz pulses via difference frequency mixing of the frequency components of an ultra-short pulse]]
[[Image:THz_OR.png|thumb|300px|THz "Optical-rectification" generates broadband THz pulses via difference frequency mixing of the frequency components of an ultra-short pulse]]
OR is more properly though of as difference frequency mixing. In a NLO material, the polarization induced by an AC electric field will not reverse its sign at the same time as the driving field, leading to a nonlinear polarization and thus frequency mixing.  If the field is applied with a femptosecond laser pulse, with a large spectral bandwidth, difference frequency mixing of different frequency components results in electromagnetic waves in the terahertz region. This is the optical analog of the audible beat frequency generated by two struck tuning forks. The emitted field is related to the polarization, <em>P</em>, by
OR is more properly though of as difference frequency mixing. In a NLO material, the polarization induced by an AC electric field will not reverse its sign at the same time as the driving field, leading to a nonlinear polarization and thus frequency mixing.  If the field is applied with a femptosecond laser pulse, with a large spectral bandwidth, difference frequency mixing of different frequency components results in electromagnetic waves in the terahertz region. This is the optical analog of the audible beat frequency generated by two struck tuning forks. The emitted field is related to the polarization, <em>P</em>, by
Line 37: Line 39:
The efficiency of THz generation depends on the second order nonlinear susceptibility of the medium. Popular materials include: inorganic NLO crystals (e.g. ZnTe, GaP), organic NLO crystals (e.g. DAST), NLO guest-host electro-optic (EO) polymers.
The efficiency of THz generation depends on the second order nonlinear susceptibility of the medium. Popular materials include: inorganic NLO crystals (e.g. ZnTe, GaP), organic NLO crystals (e.g. DAST), NLO guest-host electro-optic (EO) polymers.
See [[Second-order_Processes#Sum_and_Difference_Frequency_Generation|Sum and Difference Frequency Generation]]
See [[Second-order_Processes#Sum_and_Difference_Frequency_Generation|Sum and Difference Frequency Generation]]
<br clear='all'>


===Free-Space Electro-Optic Sampling===
[[Image:FSEOS_of_THz.png|thumb|300px|Free-space electro-optic sampling experimental schematic]]
[[Image:FSEOS_of_THz.png|thumb|300px|Free-space electro-optic sampling experimental schematic]]
In free-space electro-optic sampling (FSEOS), the THz waveform and a ultra-short "probe" pulse propagate collinearly through an EO medium. In the absence of the THz pulse, the "probe" pulse has a linear polarization that it changed to be circular by the compensator and is separated into s- and p- components by the Wollaston polarizing beam splitter. For equal s- & p- components, the balanced photodiodes produce null current. In the presence of the THz field, the EO medium becomes birefringent through the Pockel effect, and the polarization of the probe is rotated. The imbalance in s- and p- polarization causes a current, proportional to the THz field and direction, to flow from the balanced photodoides. Again, a delay stage allows for the one pulse to be moved in time with respect to the other, such that the THz waveform is sampled by the "probe" pulse. The detected current, <math>I_{det}</math> is related to the optical index, <em>n</em>, effective EO coefficient, <math>r_{eff}</math>, and sensor thickness, <em>d</em> by  
In free-space electro-optic sampling (FSEOS), the THz waveform and a ultra-short "probe" pulse propagate collinearly through an EO medium. In the absence of the THz pulse, the "probe" pulse has a linear polarization that it changed to be circular by the compensator and is separated into s- and p- components by the Wollaston polarizing beam splitter. For equal s- & p- components, the balanced photodiodes produce null current. In the presence of the THz field, the EO medium becomes birefringent through the Pockel effect, and the polarization of the probe is rotated. The imbalance in s- and p- polarization causes a current, proportional to the THz field and direction, to flow from the balanced photodoides. Again, a delay stage allows for the one pulse to be moved in time with respect to the other, such that the THz waveform is sampled by the "probe" pulse. The detected current, <math>I_{det}</math> is related to the optical index, <em>n</em>, effective EO coefficient, <math>r_{eff}</math>, and sensor thickness, <em>d</em> by  
<center><math>I_{det}\propto n^{3}r_{eff} d E_{THz}</math></center>
<center><math>I_{det}\propto n^{3}r_{eff} d E_{THz}</math></center>
Line 47: Line 49:




[[Image:THz_exp_setup.png|thumb|400px|THz time-domain spectrometer experimental schematic]]
 
In a typical experimental setup a sub-100 fs "pump" laser pulse travels through a second-order NLO, i.e. electro-optic (EO), material which generates THz by optical rectification. The radiation is collected and focused with front-surface mirrors and directed towards to detector, where it is overlapped collinearly with the sampling, "probe" beam. The probe is separated into s- and p- polarization  components using a wollaston polarizing beam splitter. The two component polarization beams are directed into balanced photo-diodes, which yield null current for equal s- and p- beam intensities. The THz electric field induces a change in the index of refraction of the EO sensor material via the electrooptic effect, rotating the "probe" polarization. This produces unequal s- and p- beam intensities, leading to current flow proportional to the THz electric field amplitude and direction.  Delay stages are used to change the delay between the THz and "probe" beams, allowing the "probe" to sample the THz waveform. The shape of the recorded current matches the THz waveform, i.e. the electric field of the THz pulse.  
In a typical experimental setup a sub-100 fs "pump" laser pulse travels through a second-order NLO, i.e. electro-optic (EO), material which generates THz by optical rectification. The radiation is collected and focused with front-surface mirrors and directed towards to detector, where it is overlapped collinearly with the sampling, "probe" beam. The probe is separated into s- and p- polarization  components using a wollaston polarizing beam splitter. The two component polarization beams are directed into balanced photo-diodes, which yield null current for equal s- and p- beam intensities. The THz electric field induces a change in the index of refraction of the EO sensor material via the electrooptic effect, rotating the "probe" polarization. This produces unequal s- and p- beam intensities, leading to current flow proportional to the THz electric field amplitude and direction.  Delay stages are used to change the delay between the THz and "probe" beams, allowing the "probe" to sample the THz waveform. The shape of the recorded current matches the THz waveform, i.e. the electric field of the THz pulse.  


<br clear='all'>
<br clear='all'>


=== EO Polymers for THz===
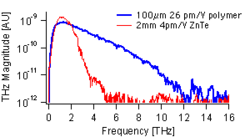
== EO Polymers for THz==
[[Image:THz_Polymer_vs_ZnTe.png‎ |thumb|250px| Poor phase matching due to a 5.3 THz phonon limits the bandwidth available using the inorganic crystal ZnTe as a THz sensor. Improved phase matching and a coherence length of 50 <math>\mu</math>m at 10 THz allows for broadband THz detection in this EO polymer ]]
[[Image:THz_Polymer_vs_ZnTe.png‎ |thumb|250px| Poor phase matching due to a 5.3 THz phonon limits the bandwidth available using the inorganic crystal ZnTe as a THz sensor. Improved phase matching and a coherence length of 50 <math>\mu</math>m at 10 THz allows for broadband THz detection in this EO polymer ]]
EO poled guest-host polymers have the potential to acheive orders of magnitude higher optical nonlinearities than crystalline materials. Poled polymers have acheived electro-optic coefficients >400 pm/V, which is two orders of magnitude larger than the inorganic crystal ZnTe, a standard material for THz generation and detection. The tunable optical and NLO properties of poled polymers, along with good phase matching, makes them valuable for THz applications.<ref>A. M. Sinyukov, L. M. Hayden, J. Phys. Chem. B 108, 8515-8522 (2004)</ref> For example, poled polymers have been used to achieve a broad bandwidth THz system at telecommunications wavelengths,<ref>C. V. McLaughlin, et al., Appl. Phys. Lett. 92, 151107 (2008)</ref> where compact laser systems are available.  Due to their relatively flat THz index of refraction, proper choice of the "pump" wavelength would allow for phase matching across the THz band even for very thick polymers.
EO poled guest-host polymers have the potential to acheive orders of magnitude higher optical nonlinearities than crystalline materials. Poled polymers have acheived electro-optic coefficients >400 pm/V, which is two orders of magnitude larger than the inorganic crystal ZnTe, a standard material for THz generation and detection. The tunable optical and NLO properties of poled polymers, along with good phase matching, makes them valuable for THz applications.<ref>A. M. Sinyukov, L. M. Hayden, J. Phys. Chem. B 108, 8515-8522 (2004)</ref> For example, poled polymers have been used to achieve a broad bandwidth THz system at telecommunications wavelengths,<ref>C. V. McLaughlin, et al., Appl. Phys. Lett. 92, 151107 (2008)</ref> where compact laser systems are available.  Due to their relatively flat THz index of refraction, proper choice of the "pump" wavelength would allow for phase matching across the THz band even for very thick polymers.
Line 66: Line 68:


<math>n_{grp}=n_{opt}-\lambda_{opt}\partial n_{opt}/\partial\lambda_{opt}</math></center>
<math>n_{grp}=n_{opt}-\lambda_{opt}\partial n_{opt}/\partial\lambda_{opt}</math></center>
where <em>c</em> is the speed of light, <math>\omega = 2 \pi f</math>, <em>f</em> is the THz frequency, <math>\lambda_{opt}</math> is the "pump" wavelength, and <math>n_{opt}</math> and <math>n_{THz}</math> are the optical and THz indices of refraction of the NLO medium.  For thicker emitters, destructive interference occurs between newly generated THz pulses and those generated earlier in the material, reducing the amplitude at the mismatched frequencies. Due to phonon lattice resonances in the THz regime, NLO crystals can be quite dispersive across this band. Many crystals are also disperive in the visible and near infrared (NIR). Polymers have very low dispersion. Their NIR and THz indices of refraction are nearly the same, yielding very good phase matching and allowing for broadband THz generation.<ref>“Organic broadband terahertz sources and sensors”, X. Zheng, et. al., J. Nanoelect. Optoelect. 2, 58-76 (2007).</ref>
where <em>c</em> is the speed of light, <math>\omega = 2 \pi f</math>, <em>f</em> is the THz frequency, <math>\lambda_{opt}</math> is the "pump" wavelength, and <math>n_{opt}</math> and <math>n_{THz}</math> are the optical and THz indices of refraction of the NLO medium.  For thicker emitters, destructive interference occurs between newly generated THz pulses and those generated earlier in the material, reducing the amplitude at the mismatched frequencies. Due to phonon lattice resonances in the THz regime, NLO crystals can be quite dispersive across this band. Many crystals are also disperive in the visible and near infrared (NIR). Polymers have very low dispersion. Their NIR and THz indices of refraction are nearly the same, yielding very good phase matching and allowing for broadband THz generation.<ref>X. Zheng, et. al., J. Nanoelect. Optoelect. 2, 58-76 (2007).</ref>




Line 72: Line 74:


== Spectroscopy Applications ==
== Spectroscopy Applications ==
[[Image:OPTP.png|thumb|600px|Time domain spectroscopy and Optical pump THz Probe compared ]]
[[Image:THz_exp_setup.png|thumb|400px|THz time-domain spectrometer experimental schematic]]
When THz radiation passes through an object its dielectric properties can be revealed.
THz radiation is commonly used for spectroscopic applications to elucidate the far-infrared properties of a variety of material systems.  THz is used for variety of spectroscopic techniques e.g. transmission and reflection mode time-domain spectroscopy, optical-pump THz-probe spectroscopy, attenuated total reflectance, near-field scanning optical microscopy, etc.
 
The appeal of THz for spectroscopy is mainly:
*coherent detection provides access to the electric field and thus the determination of the complex dielectric properties without the need for Kramers-Kronig analysis
*the low energy radiation has good penetration through non-conductive, non-polar materials
*low frequency oscillations correspond to phonon modes, molecular vibrations, and other collective oscillations which are unique to many materials and dynamic processes
*carrier scattering rates typically lay between 1-100 THz, providing useful information on charge carrier transport in conductive and photoconductive materials
 
see e.g. "THz Spectroscopy: Principals and Applications," Edited by S. Dexheimer, CRC press (2008)
<br clear='all'>
<br clear='all'>
=== THz Time Domain Spectroscopy ===
=== THz Time Domain Spectroscopy ===
[[Image:TDS_cartoon.png|thumb|300px|In THz Time Domain Spectroscopy, a ~1ps single-cycle THz pulse is propagated through a sample.]]
In THz-TDS, the transmission of the THz waveform (electric field) through a sample is measured and compared to a reference, typically the transmission through the experiment without a sample present.  Modeling normal incidence transmission through the sample with Fresnel coefficients,<ref>L. Duvillaret, et al., IEEE J. Quant. Elect. 2, 739 (1996)</ref> and assuming <math>\kappa << n</math>, the index of refraction, <em>n</em>, and the power absorption coefficient <math>\alpha</math> are
<center><math>n(\nu)\approx1+\frac{c}{d\omega}\left|\Delta\Phi \right|</math></center>


[[Image:TDS_cartoon.png|thumb|300px|In THz Time Domain Spectroscopy, a ~1ps single-cycle THz pulse is propagated through a sample.]]
<center><math>\alpha(\nu)\approx-\frac{1}{2 d}ln\left(\frac{1}{T}\frac{Mag_{sample}}{Mag_{ref}} \right)</math></center>
The electric field of the THz pulse is sampled via the electrooptic effect in a second order nonlinear material.


The field transmitted through the sample is compared to that transmitted through its substrate (or through free space for free standing samples) and through fourier analysis the frequency dependent index of refraction and absorption coefficients are extracted.
where <math>\omega = 2\pi\nu</math>, <math>\alpha =\omega \kappa / 2 c</math>, <em>d</em> is the sample thickness, <em>c</em> is the speed of light, <em>T</em> are the Fresnel transmission coefficients to correct for reflective losses, <math>\Delta\Phi</math> is the measured change in THz phase, and <math>Mag_{sample}</math> is the magnitude of the THz transmission through the sample.


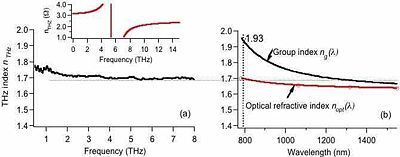
[[Image:TDS_APC.png|thumb|300px|The index of refraction of amorphous polycarbonate from 0-7THz.]]
[[Image:TDS_APC.png|thumb|300px|The index of refraction of amorphous polycarbonate from 0-7THz.]]
The extracted index of refraction and absorption can be of interest for a number of reasons.  Typically, its frequency dependence can be modeled to extract information about the underlying physics. If the material is of interest to THz optics, knowledge of its optical properties are vital.  For example, knowledge of the THz index of refraction of a material of interest for THz emission and detection is needed to determine phase matching conditions.
The complex dielectric function can also be computed from the index of refraction and absorption coefficient. If the material is conducting, the complex conductivity can also be computed. This allows for conductivity models to be applied  to model the frequency dependence and describe the underlying charge carrier motion.


<br clear='all'>
<br clear='all'>
Line 89: Line 103:
[[Image:OPTP_cartoon.png|thumb|300px|In Optical-Pump THz-Probe Spectroscopy, a THz pulse is propagated through a photo-excited sample.]]  
[[Image:OPTP_cartoon.png|thumb|300px|In Optical-Pump THz-Probe Spectroscopy, a THz pulse is propagated through a photo-excited sample.]]  


In Optical Pump THz Probe Spectroscopy (OPTP) the THz waveform transmitted through the excited sample is compared to that transmitted through the unexcited sample and through fourier analysis the full frequency dependent complex conductivity can be obtained. Modeling on this photo-induced conductivity yields the mobility and carrier density, also giving the photon-to-carrier yield. Control of the delay between the excitation (the "pump") and the THz pulse (the "probe") provides the time evolution of the photoexcited state.
In Optical-Pump THz-Probe Spectroscopy (OPTP), a.k.a. time-resolve THz spectroscopy, the THz waveform transmitted through a photo-excited sample is compared to that transmitted through the unexcited sample. Through fourier analysis, the full frequency dependent complex conductivity can be obtained. Modeling on this photo-induced conductivity, e.g. with the Drude model or a variation there of, yields the mobility and carrier density, also giving the photon-to-carrier yield. Control of the delay between the optical photo-excitation pulse (the "pump") and the THz pulse (the "probe") allows us to map out the time evolution of the photoexcited state.


[[Image:P3HT_pump_probe.png|thumb|600px|(left) Photoconductivity dynamics described by pump delay dependent changes in THz transmission through the photoexcited sample. (Right) The change in the transmitted THz waveform is recorded at various delays to allow for the extraction of the evolving frequency-dependent dielectric properties.]]
The appeal of THz for spectroscopy is mainly:
 
*Non-contact, low energy (meV), non-perturbing, optical probe with sub-ps resolution
   
*Direct access to the complex conductivity of the material system under study
To extract the complex conductivity we use the following approximate analytic relationship following the work of Sundstrum
*Sensitive to (free) charge carrier scattering (i.e. damping) rate, and low-frequency oscillation of bound-charges (e.g excitons)
<br clear='all'>
====Modes of Operation====
[[Image:P3HT_pump_probe.png|thumb|600px|(left) Photoconductivity dynamics described by pump-delay dependent changes in THz transmission through the photoexcited sample. (Right) The change in the transmitted THz waveform is recorded at various delays to allow for the extraction of the evolving frequency-dependent dielectric properties.]]
OPTP experiments can be operated, essentially, in two ways. The first, involves monitoring changes in a single point on the THz waveform as the "pump" delay stage is moved. Typically referred to as a "pump" scan, this mode allows for the average excited state dynamics to be mapped out with respect to the delay after the photo-excitation event. The other, involves recording the entire THz waveform transmitted through an excited sample at various delays after excitation. Typically referred to as a "probe" scan, this mode allows us to map the evolution of the frequency-dependent dielectric properties of the excited state.


:<math>\tilde{\sigma} (\omega) \approx - \frac {(n_{THz} +1 )}{Z_0d}\frac {\Delta \tilde{E}(\omega)}{\tilde{E}_0(\omega)}\,\!</math>
To extract the complex conductivity, a variety of models and techniques can be used,<ref>M. C. Beard, et. al., J. Appl. Phys. 90, 5915 (2001)</ref><ref>D. G. Cooke, et. al., Appl. Phys. Lett. 89, 122103 (2006)</ref><ref>X. L. Cross, et. al. IEEE Appl. Supercond. 19, 3614 (2009)</ref>  we use the following approximate analytic relationship<ref>H.-W. Nienhuys, V. Sundstrom, Phys. Rev. B 71, 235110 (2005)</ref>


where
<center><math>\tilde{\sigma} (\omega) \approx - \frac {(n_{THz} +1 )}{Z_0d}\frac {\Delta \tilde{E}(\omega)}{\tilde{E}_0(\omega)}\,\!</math></center>


:<math>d\,\!</math> is the absorption depth at &lambda;<sub>exc</sub>
where<math>d\,\!</math> is the absorption depth at &lambda;<sub>exc</sub>
<br clear='all'>
<br clear='all'>
=== Advantages ===
*Non-contact low energy (meV) non-perturbing optical probe with sub-ps resolution
*Coherent detection provides magnitude and phase of THz waveform, i.e. direct access to the complex dielectric properties of materials under study
*THz radiation is sensitive to charge carriers as carrier scattering times are fs-ps placing the scattering (damping) rate in the THz regime


=== Special Studies ===
=== Special Studies ===
Time-resolved broadband THz studies have the capability to reveal new physics concerning the nature of charge transport in polymers.  Many models of conductivity are similar over narrow bandwidths, particularly 0-2 THz (Figure 1.26, left).  Broadband (0-15 THz) OPTP will access frequency ranges where the models diverge from each other allowing a more complete understanding of the fundamental charge carrier dynamics and mechanisms.
Time-resolved broadband THz studies have the capability to reveal new physics concerning the nature of charge transport in polymers.  Many models of conductivity are similar over narrow bandwidths, particularly 0-2 THz (Figure 1.26, left).  Broadband (0-10 THz) OPTP will access frequency ranges where the models diverge from each other allowing a more complete understanding of the fundamental charge carrier dynamics and mechanisms.


<br clear='all'>
<br clear='all'>
Line 130: Line 139:


We have applied this technique to study carrier dynamics in RR-P3HT and ultrafast charge transfer in the bulk heterojunction P3HT/PCBM 1:1 excited with either 400 nm (3.1 eV) and 800 nm (1.44 eV) light, the results of which are published in J Phys Chem C.
We have applied this technique to study carrier dynamics in RR-P3HT and ultrafast charge transfer in the bulk heterojunction P3HT/PCBM 1:1 excited with either 400 nm (3.1 eV) and 800 nm (1.44 eV) light, the results of which are published in J Phys Chem C.
[[Image:OPTP_cryo.jpg|thumb|300px|Inclusion of a liquid He cryostat allowed for temperature dependent studies ]]
[[Image:P3HT_temp_dep.png|thumb|300px|Low temperature photoconductivity increase]]
<br clear='all'>
At low temperature there is an increase in the photoconductivity (mobility) of P3HT due to decreased torsoinal disorder which increases the effective conjugation length. The faster recombination dynamics are associated with inhibited interchain hopping at low temperature.
[[Image:P3ht_pcbm_uv_vis.png|thumb|300px|There is only very weak absorption at 800 nm. ]] 
[[Image:P3HT_pump.png|thumb|300px|Both energy excitations yield similar dynamics on subpicosecond time scales.]]
   
   
[[Image:ET_P3HT_to_PCBM.png|thumb|300px|Ultrafast electron transfer from P3HT to PCBM is marked by an increase in the long lived photoconductive state in the bulk heterojunction compared to neat films of P3HT.]]
[[Image:ET_P3HT_to_PCBM.png|thumb|300px|Ultrafast electron transfer from P3HT to PCBM is marked by an increase in the long lived photoconductive state in the bulk heterojunction compared to neat films of P3HT.]]


[[Image:P3HTPCBM_pump.png|thumb|300px|Bulk heterojunction compared to P3HT]]
[[Image:P3HTPCBM_pump.png|thumb|300px|Bulk heterojunction compared to P3HT]]


The extracted complex frequency-dependent conductivty of P3HT exibits characteristics of strong (Anderson) carrier localization and inhibited long range trasport due to disorder (below). Fitting of  the conductivity to the Drude-Smith model provides photon-to-carrier yields of < 1.5% and a hole mobility of ~35 cm^2/Vs. The THz regime mobility agrees well with published DFT calculations of the predicted intrinsic hole mobility in well ordered P3HT.
The extracted complex frequency-dependent conductivty of P3HT exibits characteristics of strong (Anderson) carrier localization and inhibited long range trasport due to disorder (below). Fitting of  the conductivity to the Drude-Smith model provides photon-to-carrier yields of < 1.5% and a hole mobility of ~35 cm^2/Vs. The THz regime mobility agrees well with published DFT calculations of the predicted intrinsic hole mobility in well ordered P3HT.
<br clear='all'>
<br clear='all'>
[[Image:P3HT_400nm_probe.png|thumb|300px|The complex conductivity of P3HT measured from 200 GHz - 2.1 THz extracted at 1, 1.5 and 6.2 ps after photoexcitation. The solid lines are fits to the Drude-Smith model.]]
[[Image:Order_dep_Mobility.png|thumb|300px|The mobility in perfectly ordered P3HT far exceeds that typically measured in devices due to the effect of disorder and defects. ]]


The high frequency THz radiation probes carriers over short (nanoscale) distances, which corresponds to highly ordered domains in this system. Through this experiment we are able to experimentally determine the upper limit of the carrier mobility that would be seen in a device with perfect ordering, instead of the disorder limited mobility typically seen in devices.
The high frequency THz radiation probes carriers over short (nanoscale) distances, which corresponds to highly ordered domains in this system. Through this experiment we are able to experimentally determine the upper limit of the carrier mobility that would be seen in a device with perfect ordering, instead of the disorder limited mobility typically seen in devices.

Revision as of 19:13, 1 October 2009

Previous Topic Return to Second-order Processes, Materials & Characterization Menu Next Topic


Error creating thumbnail: File with dimensions greater than 12.5 MP
1 THz ~ 300 µm wavelength ~33 wave numbers ~ 4 meV- Courtesy of www.SURA.org

Terahertz (THz) is Far-Infrared radiation located between microwaves and infrared in the electromagnetic spectrum. It is low-energy, non-ionizing radiation which can penetrate many non-polar, non-conducting materials such as clothing, paper, masonry or plastic. Possible applications of THz include:

  • Medical imaging - THz can penetrate several millimeters into tissues with low water content, or deep into teeth, without damage. For example: THz can be used for burn depth assessment, skin cancer identification, etc.
  • Security screening- THz can penetrate clothing and reveal hidden weapons. Explosives, biological agents, and controlled substances have specific spectral signatures allowing for chemical identification.
  • Spectroscopy- THz time domain spectroscopy can measure the low-energy, far-infrared properties of substances that are opaque in the visible and near-infrared regions of the spectrum. In particular, collective vibrations, phonon resonances, and scattering rates of charge carriers are typically in the THz range.
  • Manufacturing- Circuit boards, device components, and the contents of paper packages can be easily visualized for quality control. For example, THz inspections can identify voids in space shuttle foam, like those responsible for the Columbia disaster.


History of THz Science

A THz-TDS/OPTP experimental setup

Far-infrared studies have occurred since the invention of the bolometer in 1881 by astronomer Samuel Langley. Much of the early far-infrared work was done by Rubens, who discovered reststrahlen sources enabling measurements crucial to Planck's blackbody radiation theory. Far-infrared transmission studies of superconductors confirmed the energy gap predicted by Bardeen,Cooper, and Schrieffer's superconductivity theory. Since the invention of frequency-division multiplexing in 1949, Fourier-transform infrared spectroscopy became a standard tool in physical chemistry. Over the years, numerous sources and detectors have been discovered e.g. Golay cell, water-vapor laser, pyroelectric detector, synchrotrons, free-electron lasers, and quantum cascade lasers.

Modern pulsed-THz sources grew out of the work of Auston, Nuss, and Grischkowsky on photoconductive switches, electrical pulses on transmission lines, and far-infrared emission from nonlinear crystals in the 1980s. Since their pioneering work, photoconductive switches have become one of two popular methods of generation and coherent detection of bright THz pulses with high sensitivity. The other popular modern method involves generation of broadband THz radiation via "optical rectification" and coherent detection of the THz waveform through free-space electro-optic sampling, both occurring in nonlinear optical media.


THz generation and detection

THz radiation is typically generated via optical rectification (OR), of laser pulses from a single source, in a nonlinear optical (NLO) material or impulsively from photoconductive dipole antennae (PDA). Difference-frequency generation (DFG) between two different laser beams in a NLO material can also be used to generate THz radiation. PDAs can also be used to coherently detect the THz waveform, through the detected photocurrent. Second order NLO materials can be coherent detect THz pulses through the free-space electro-optic sampling (FSEOS).

Photoconductive Dipole Antennae

Schematic of photoconductive dipole antenna emitter and sensor

In a PDA, THz radiation is emitted by an ultra-fast transient photo-current created in a biased semiconductor, typically GaAs. The semiconductor is photo-excited with an ultra-short pulse to generate short-lived charges, which are accelerated with an applied electric field. The emitted field, <math>E_{THz}</math> is related to the current, J, by

<math>E_{THz}\propto\partial J/\partial t</math>

Though PDAs are bright THz sources, finite carrier lifetimes limit the bandwidth available from photoconductive materials to less than that acheivable via OR in NLO materials. Detection of the THz pulse occurs, essentially, through the opposite effect. An ultra-short pulse generates short-lived charge carriers, which are subsequently accelerated by the THz electric field. This generates a transient current between two electrodes, which is proportional to the amplitude and direction of the THz electric field making this a coherent detection technique. A delay stage allows for the one pulse to be moved in time with respect to the other, similar to a correlation, such that the THz waveform is sampled point-by-point by the "probe" pulse

Optical Rectification in a Nonlinear Optical Medium

THz "Optical-rectification" generates broadband THz pulses via difference frequency mixing of the frequency components of an ultra-short pulse

OR is more properly though of as difference frequency mixing. In a NLO material, the polarization induced by an AC electric field will not reverse its sign at the same time as the driving field, leading to a nonlinear polarization and thus frequency mixing. If the field is applied with a femptosecond laser pulse, with a large spectral bandwidth, difference frequency mixing of different frequency components results in electromagnetic waves in the terahertz region. This is the optical analog of the audible beat frequency generated by two struck tuning forks. The emitted field is related to the polarization, P, by

<math>E_{THz}\propto\partial^{2} P/\partial t^{2}</math>

The efficiency of THz generation depends on the second order nonlinear susceptibility of the medium. Popular materials include: inorganic NLO crystals (e.g. ZnTe, GaP), organic NLO crystals (e.g. DAST), NLO guest-host electro-optic (EO) polymers. See Sum and Difference Frequency Generation

Free-Space Electro-Optic Sampling

Free-space electro-optic sampling experimental schematic

In free-space electro-optic sampling (FSEOS), the THz waveform and a ultra-short "probe" pulse propagate collinearly through an EO medium. In the absence of the THz pulse, the "probe" pulse has a linear polarization that it changed to be circular by the compensator and is separated into s- and p- components by the Wollaston polarizing beam splitter. For equal s- & p- components, the balanced photodiodes produce null current. In the presence of the THz field, the EO medium becomes birefringent through the Pockel effect, and the polarization of the probe is rotated. The imbalance in s- and p- polarization causes a current, proportional to the THz field and direction, to flow from the balanced photodoides. Again, a delay stage allows for the one pulse to be moved in time with respect to the other, such that the THz waveform is sampled by the "probe" pulse. The detected current, <math>I_{det}</math> is related to the optical index, n, effective EO coefficient, <math>r_{eff}</math>, and sensor thickness, d by

<math>I_{det}\propto n^{3}r_{eff} d E_{THz}</math>

As the recorded current is proportional to the time-dependent THz electric field, this is also a coherent detection technique. See Electro-optic effects


In a typical experimental setup a sub-100 fs "pump" laser pulse travels through a second-order NLO, i.e. electro-optic (EO), material which generates THz by optical rectification. The radiation is collected and focused with front-surface mirrors and directed towards to detector, where it is overlapped collinearly with the sampling, "probe" beam. The probe is separated into s- and p- polarization components using a wollaston polarizing beam splitter. The two component polarization beams are directed into balanced photo-diodes, which yield null current for equal s- and p- beam intensities. The THz electric field induces a change in the index of refraction of the EO sensor material via the electrooptic effect, rotating the "probe" polarization. This produces unequal s- and p- beam intensities, leading to current flow proportional to the THz electric field amplitude and direction. Delay stages are used to change the delay between the THz and "probe" beams, allowing the "probe" to sample the THz waveform. The shape of the recorded current matches the THz waveform, i.e. the electric field of the THz pulse.


EO Polymers for THz

Poor phase matching due to a 5.3 THz phonon limits the bandwidth available using the inorganic crystal ZnTe as a THz sensor. Improved phase matching and a coherence length of 50 <math>\mu</math>m at 10 THz allows for broadband THz detection in this EO polymer

EO poled guest-host polymers have the potential to acheive orders of magnitude higher optical nonlinearities than crystalline materials. Poled polymers have acheived electro-optic coefficients >400 pm/V, which is two orders of magnitude larger than the inorganic crystal ZnTe, a standard material for THz generation and detection. The tunable optical and NLO properties of poled polymers, along with good phase matching, makes them valuable for THz applications.[1] For example, poled polymers have been used to achieve a broad bandwidth THz system at telecommunications wavelengths,[2] where compact laser systems are available. Due to their relatively flat THz index of refraction, proper choice of the "pump" wavelength would allow for phase matching across the THz band even for very thick polymers.

See Poling Polymers Basics


Phase (velocity) matching by comparing the THz (a) and the visible (b) indices of refraction of EO poled polymers. The Lorentz Oscillator model of the THz index of ZnTe is included in the inset of (a) for reference.


Phase matching (i.e. velocity matching) is necessary for efficient THz generation and detection. For efficient energy transfer between the optical and THz pulses, they should travel through the NLO medium at the same velocity. The distance over which the THz and optical travel in phase is the coherence length, <math>l_{c}</math>,

<math>l_{c}=\frac{\pi c}{\omega\left|n_{grp}-n_{THz}\right|}</math> <math>n_{grp}=n_{opt}-\lambda_{opt}\partial n_{opt}/\partial\lambda_{opt}</math>

where c is the speed of light, <math>\omega = 2 \pi f</math>, f is the THz frequency, <math>\lambda_{opt}</math> is the "pump" wavelength, and <math>n_{opt}</math> and <math>n_{THz}</math> are the optical and THz indices of refraction of the NLO medium. For thicker emitters, destructive interference occurs between newly generated THz pulses and those generated earlier in the material, reducing the amplitude at the mismatched frequencies. Due to phonon lattice resonances in the THz regime, NLO crystals can be quite dispersive across this band. Many crystals are also disperive in the visible and near infrared (NIR). Polymers have very low dispersion. Their NIR and THz indices of refraction are nearly the same, yielding very good phase matching and allowing for broadband THz generation.[3]



Spectroscopy Applications

THz time-domain spectrometer experimental schematic

THz radiation is commonly used for spectroscopic applications to elucidate the far-infrared properties of a variety of material systems. THz is used for variety of spectroscopic techniques e.g. transmission and reflection mode time-domain spectroscopy, optical-pump THz-probe spectroscopy, attenuated total reflectance, near-field scanning optical microscopy, etc.

The appeal of THz for spectroscopy is mainly:

  • coherent detection provides access to the electric field and thus the determination of the complex dielectric properties without the need for Kramers-Kronig analysis
  • the low energy radiation has good penetration through non-conductive, non-polar materials
  • low frequency oscillations correspond to phonon modes, molecular vibrations, and other collective oscillations which are unique to many materials and dynamic processes
  • carrier scattering rates typically lay between 1-100 THz, providing useful information on charge carrier transport in conductive and photoconductive materials

see e.g. "THz Spectroscopy: Principals and Applications," Edited by S. Dexheimer, CRC press (2008)

THz Time Domain Spectroscopy

In THz Time Domain Spectroscopy, a ~1ps single-cycle THz pulse is propagated through a sample.

In THz-TDS, the transmission of the THz waveform (electric field) through a sample is measured and compared to a reference, typically the transmission through the experiment without a sample present. Modeling normal incidence transmission through the sample with Fresnel coefficients,[4] and assuming <math>\kappa << n</math>, the index of refraction, n, and the power absorption coefficient <math>\alpha</math> are

<math>n(\nu)\approx1+\frac{c}{d\omega}\left|\Delta\Phi \right|</math>
<math>\alpha(\nu)\approx-\frac{1}{2 d}ln\left(\frac{1}{T}\frac{Mag_{sample}}{Mag_{ref}} \right)</math>

where <math>\omega = 2\pi\nu</math>, <math>\alpha =\omega \kappa / 2 c</math>, d is the sample thickness, c is the speed of light, T are the Fresnel transmission coefficients to correct for reflective losses, <math>\Delta\Phi</math> is the measured change in THz phase, and <math>Mag_{sample}</math> is the magnitude of the THz transmission through the sample.

The index of refraction of amorphous polycarbonate from 0-7THz.

The extracted index of refraction and absorption can be of interest for a number of reasons. Typically, its frequency dependence can be modeled to extract information about the underlying physics. If the material is of interest to THz optics, knowledge of its optical properties are vital. For example, knowledge of the THz index of refraction of a material of interest for THz emission and detection is needed to determine phase matching conditions. The complex dielectric function can also be computed from the index of refraction and absorption coefficient. If the material is conducting, the complex conductivity can also be computed. This allows for conductivity models to be applied to model the frequency dependence and describe the underlying charge carrier motion.


Optical Pump THz Probe Spectroscopy

In Optical-Pump THz-Probe Spectroscopy, a THz pulse is propagated through a photo-excited sample.

In Optical-Pump THz-Probe Spectroscopy (OPTP), a.k.a. time-resolve THz spectroscopy, the THz waveform transmitted through a photo-excited sample is compared to that transmitted through the unexcited sample. Through fourier analysis, the full frequency dependent complex conductivity can be obtained. Modeling on this photo-induced conductivity, e.g. with the Drude model or a variation there of, yields the mobility and carrier density, also giving the photon-to-carrier yield. Control of the delay between the optical photo-excitation pulse (the "pump") and the THz pulse (the "probe") allows us to map out the time evolution of the photoexcited state.

The appeal of THz for spectroscopy is mainly:

  • Non-contact, low energy (meV), non-perturbing, optical probe with sub-ps resolution
  • Direct access to the complex conductivity of the material system under study
  • Sensitive to (free) charge carrier scattering (i.e. damping) rate, and low-frequency oscillation of bound-charges (e.g excitons)


Modes of Operation

Error creating thumbnail: Unable to save thumbnail to destination
(left) Photoconductivity dynamics described by pump-delay dependent changes in THz transmission through the photoexcited sample. (Right) The change in the transmitted THz waveform is recorded at various delays to allow for the extraction of the evolving frequency-dependent dielectric properties.

OPTP experiments can be operated, essentially, in two ways. The first, involves monitoring changes in a single point on the THz waveform as the "pump" delay stage is moved. Typically referred to as a "pump" scan, this mode allows for the average excited state dynamics to be mapped out with respect to the delay after the photo-excitation event. The other, involves recording the entire THz waveform transmitted through an excited sample at various delays after excitation. Typically referred to as a "probe" scan, this mode allows us to map the evolution of the frequency-dependent dielectric properties of the excited state.

To extract the complex conductivity, a variety of models and techniques can be used,[5][6][7] we use the following approximate analytic relationship[8]

<math>\tilde{\sigma} (\omega) \approx - \frac {(n_{THz} +1 )}{Z_0d}\frac {\Delta \tilde{E}(\omega)}{\tilde{E}_0(\omega)}\,\!</math>

where<math>d\,\!</math> is the absorption depth at λexc

Special Studies

Time-resolved broadband THz studies have the capability to reveal new physics concerning the nature of charge transport in polymers. Many models of conductivity are similar over narrow bandwidths, particularly 0-2 THz (Figure 1.26, left). Broadband (0-10 THz) OPTP will access frequency ranges where the models diverge from each other allowing a more complete understanding of the fundamental charge carrier dynamics and mechanisms.


Carrier Dynamics

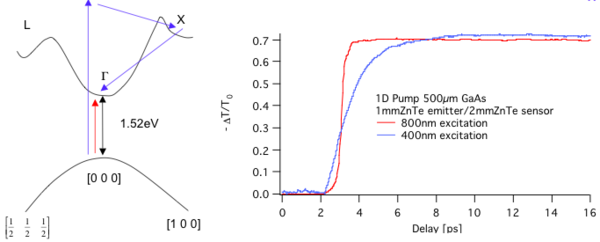
Excitation at 800nm vs 400nm. (Left) A band diagram of GaAs shows that the excess 1.49eV provided by the 400nm excitation allows carriers to scatter to higher valleys. (Right) The longer rise time of the 400nm photo-induced conductivity signal corresponds to the time required for carriers to return to the high mobility gamma valley.

OPTP spectroscopy has be used to examine carrier dynamics, Drude-like and deviations from the Drude model in popular semiconductors such as semi-insulating (SI-) GaAs


File:GaAs 800sigma.png
The frequency-dependent photoconductivity of GaAs shows deviations from the simple Drude model.


Carrier trapping

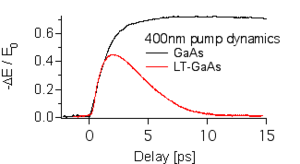
comparison of the photo- conductivity of low-temperature grown (LT-) GaAs with SI-GaAs

It can also be used to identify carrier trapping. The rapid decrease in THz absorption (below) in photoexcited LT-GaAs is due to carrier trapping by As clusters.

We have applied this technique to study carrier dynamics in RR-P3HT and ultrafast charge transfer in the bulk heterojunction P3HT/PCBM 1:1 excited with either 400 nm (3.1 eV) and 800 nm (1.44 eV) light, the results of which are published in J Phys Chem C.

Error creating thumbnail: Unable to save thumbnail to destination
Ultrafast electron transfer from P3HT to PCBM is marked by an increase in the long lived photoconductive state in the bulk heterojunction compared to neat films of P3HT.
Error creating thumbnail: Unable to save thumbnail to destination
Bulk heterojunction compared to P3HT

The extracted complex frequency-dependent conductivty of P3HT exibits characteristics of strong (Anderson) carrier localization and inhibited long range trasport due to disorder (below). Fitting of the conductivity to the Drude-Smith model provides photon-to-carrier yields of < 1.5% and a hole mobility of ~35 cm^2/Vs. The THz regime mobility agrees well with published DFT calculations of the predicted intrinsic hole mobility in well ordered P3HT.

The high frequency THz radiation probes carriers over short (nanoscale) distances, which corresponds to highly ordered domains in this system. Through this experiment we are able to experimentally determine the upper limit of the carrier mobility that would be seen in a device with perfect ordering, instead of the disorder limited mobility typically seen in devices.

External Links

See Wikipedia Terahertz Radiation

See Wikipedia Terahertz time-domain spectroscopy

See Wapedia Terahertz

See THz Group Wiki- password required THz Polymers Wiki


References

  1. ↑ A. M. Sinyukov, L. M. Hayden, J. Phys. Chem. B 108, 8515-8522 (2004)
  2. ↑ C. V. McLaughlin, et al., Appl. Phys. Lett. 92, 151107 (2008)
  3. ↑ X. Zheng, et. al., J. Nanoelect. Optoelect. 2, 58-76 (2007).
  4. ↑ L. Duvillaret, et al., IEEE J. Quant. Elect. 2, 739 (1996)
  5. ↑ M. C. Beard, et. al., J. Appl. Phys. 90, 5915 (2001)
  6. ↑ D. G. Cooke, et. al., Appl. Phys. Lett. 89, 122103 (2006)
  7. ↑ X. L. Cross, et. al. IEEE Appl. Supercond. 19, 3614 (2009)
  8. ↑ H.-W. Nienhuys, V. Sundstrom, Phys. Rev. B 71, 235110 (2005)
Previous Topic Return to Second-order Processes, Materials & Characterization Menu Next Topic
Retrieved from "http://cleanenergywiki.org/index.php?title=Terahertz_Radiation&oldid=5196"