Structure-Property Relationships
| Previous Topic | Return to Second-order Processes, Materials & Characterization Menu | Next Topic |
Bond order alternation (BOA) and bond length alternation (BLA) are useful concepts that can be correlated to α the linear polarizability and β the first hyperpolarizability of molecules. The effect of applied electrical fields on BOA and BLA can be predicted by understanding the chemical structure and how charge distribution and dipole moment will shift.
Applying theory to relate structure to properties
Material chemists help bring theory to play with the rational design of molecules.
The sum over states expression for β describes the factors for building a molecule with high β. This can be translated into an optimized molecule, which can then be incorporated into an optimized material.
See Meyers 1994 [1]
Bond Length Alternation
Bond length alternation is a construct that can be used to monitor the amount of polarization in a molecule. Bond-length alternation (BLA) is defined as the average of the difference in the length between adjacent carbon-carbon bonds in a polymethine ((CH)n) chain. A polymethine dye is a series of CH units connected by double or single bonds.
Bond-length alternation (BLA) is defined as the average of the difference in the length between adjacent carbon-carbon bonds in a polymethine ((CH)n) chain. Polyenes (such as ethylene) have alternating C-C double (1.34 Å), the carbon bond in ethane (1.54 Å) and single bonds between two sp2 hybridized carbons in a polyene is (1.45 Å). As you move from butadiene to polyacetylene the double bonds a bit longer and the single bonds become a little shorter. The average difference between single and double bond lengths is the bond length alternation (BLA), for polyenes show a high degree of BLA (+ 0.11 Å). If instead of a structural view we wish to consider an electronic or molecular orbital related parameter we can consider bond order. A double bond has a bond order of 2 and single bond has a bond order of one. The bond order alternation is -1 (1-2=-1). If you attach a donor and acceptor group to opposite ends of the molecule donor will attempt to transfer electrons to the acceptor by pushing electrons into the chain.
A simple model has been proposed recently where α, β and γ are correlated with the degree of ground-state polarization.
The degree of ground-state polarization, or in other words the degree of charge separation in the ground state, depends primarily on the chemical structure (for example, the structure of the π-conjugated system, or the strength of the donor and acceptor substituents), but also on its surroundings (for example, the polarity of the medium).
In donor-acceptor polyenes, this variable is related to a geometrical parameter, the bond-length alternation (BLA)
Resonance Structures and BLA
It is illustrative to discuss the wave function of the ground state in terms of a linear combination of the two limiting resonance structures:
- a neutral form characterized by a positive BLA and
- a charge-separated form characterized by a negative BLA (since the double and single bond pattern is now reversed relative to the neutral form).
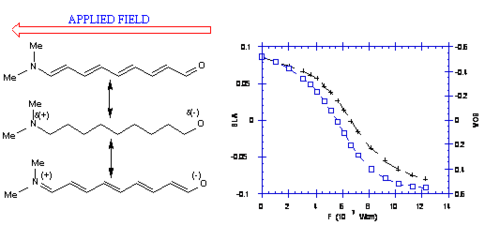
From an energetic standpoint the two resonance structures can be treated as having two potential wells separated by a nuclear coordinate. The first resonance structure on the left has a BLS of .11. Using the same carbon numbering scheme first molecule on the right would have a BLA of -.11 because the double bonds in the center are shifted right one carbon atom. The neutral molecule has a lower potential energy and therefore will the more favored state. The potential energy diagram shows a higher energy curve for the charge separated resonance structure and a dotted line shows the mixing state. The ground of this is a resonance structure that looks more like the neutral molecule. For substituted polyenes with weak donors and acceptors, the neutral resonance form dominates the ground-state wave function, and the molecule has a high degree of BLA.
This is visualized by the relative size of the two balloons over the equilibrium arrow, (this is not a representation of the molecule itself).
By adding a donor group on the right and acceptor on the left you decrease the energy difference between the two forms thus stabilizing the molecule. The relative contribution of the two forms to the resonance structure becomes more equal. The bond length alternation will decrease and the molecule will look less polyene like and more zwitterionic (charge separated). With stronger donors and acceptors, the contribution of the charge-separated resonance form to the ground state increases and simultaneously, BLA decreases.
In the bottom structure we replace the C=O with a C=N+ (an iminium group) which is a stronger charge acceptor. The electrons move from one side to the other. The structure on the right is an identical to the structure on the left. The charge will be equally distributed between the two nitrogens resulting in 1.5 bonds between all carbons. The two forms have the same energy. When the two resonance forms contribute equally to the ground-state structure, the molecule exhibits essentially no BLA. This zero BLA limit is the so-called cyanine limit. The position of the electron will be more sensitive to the electric field in the cyanine case; this is also known as polarizability.
Second order optical materials require asymmetrical polarizability. Neither the first case with total transfer (polyene limit) and or the last case with equal transfer (cyanine limit) will have asymmetry; they will not have no β. The middle molecule will has some asymmetrical polarizability. Starting at the polyene limit or the cyanine limit you can add weak acceptors and thereby increase the asymmetry, and the β increases. The curve of β vs bond length alternation will start at zero, go up to a peak and then go back down to zero. For example, with stilbene and paranitroaniline and add stronger donors and acceptor groups, or make the molecules longer, you can increase the β. However, past a certain point stronger donors and acceptors simply results in a zwitterion and the polarizability decreases. The optimal point can be described and predicted this using quantum mechanics and four orbitals.
Electric Field Perturbation of Structure
To move electrons from one end to another it requires a very large electric field (107 volts per cm) on the order of the energy that holds the molecule together. These fields are about 100 larger than are typically used in a laboratory. You can plot the BLA and the Bond order alternation (BOA) as well as the induced dipole moment. This molecule does not start at the polyene limit for BLA of .11 because there first molecule already has a donor and acceptor groups. The BLA starts at .08 and as the field is increase it goes down to zero and then becomes negative. The bond order alternative (BOA) starts negative, goes to zero and then becomes positive. The change with respect to electric field is greatest in the center of the curve near zero BLA or BOA. An electric field can increase charge separation in the ground –state of molecules. This in turn modifies the BLA, the Bond Order Alternation (BOA) and the dipole moment.
As you move from no electric field to a large electric field (shown as 0, 5 and 8 x 107 V/cm) there is an increase in positive charge on one end (the nitrogen end) and an increase in negative charge on the other end (the oxygen end).
<swf width="550" height="400">images/1/12/Boa.swf</swf>
In the above animation see what happens to the electron density distribution as you apply an electric field using the bar on the right.
Dipole Moment vs. Field and BOA
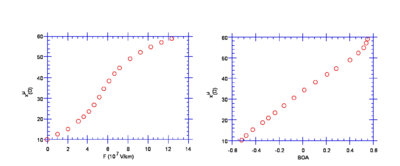
As a consequence of the charge redistribution, the dipole moment increases as a function of the applied electric field. Since the BOA is a function of field and the dipole moment is a function of field one can now correlate the dipole with the BOA to develop our first structure (BOA)- property (dipole moment) relationship.
The dipole moment versus electric field goes up and then saturates. The mathematical definition of polarizability is Dμ DE; the slope of any function at any given point. The slope increases and then decreases. The slope is highest around 30-40 μ
A plot of dipole vs BOA going from a polyene to a cyanine is approximately a straight line because both the dipole and the BOA are sigmoidal curves. Around zero BOA (the cyanine limit) the polarizability is largest. The second derivative of this curve is the first hyperpolizability.
Linear Polarizability and BOA
- <math>\alpha \propto \left ( \frac {\mu^{2}_{ge}}{E_{ge}}\right )\,\!</math>
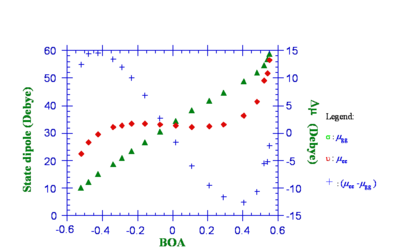
A linear polarizability α(alpha) vs BOA curve starts small, increases to a maximum and then goes down. A graph of polarizability vs charge is a sigmoidal curve so the maximum slope of such a curve occurs near the inflection point where BOA is zero. The polarizability is highest at the cyanine limit, and the hyperpolarizability is zero at the cyanine limit. Rate of change of polarizability is zero at the cyanine limit and from a particle- in-a-box perspective the molecule does not have an asymmetrical polarizability. Thus without any sum-over-states calculations you can draw conclusions about the linear polarizability and hyperpolarizability using only ground state dipole moment calculations.
In a sum-over-states calculation the linear polarizability is defined as the sum over the square of all of the transition dipole moments, between the ground and any of the excited states, divided by the energy gap. The result is the red curve which peaks at the cyanine limit. Spectroscopically molecules like these usually have a single strong peak which has a transition dipole moment that is larger than others and that peak tends to be the lowest energy, resulting in a larger energy gap.
In a two state model we choose to ignore the contribution from all terms except the one that give rise to the strong peak. α is the transition dipole moment squared between the ground and one excited state, over the energy gap between these two states results in the blue open circles. This matches the red curve very well so the two state model seems to capture the essence of the relationship. The question is which term is responsible for the peak; is it the transition dipole moment (blue triangle) or one over the energy gap (blue square)? Calculating and plotting these two terms shows that both peak near the cyanine limit. As a result the polarizabilty peaks at the cyanine limit.
First Hyper-polarizability and BOA
By calculating β (beta) for each electric field and differing BOA and taking into account all the states it shows that β goes up, peaks about halfway between the polyene and the cyanine limit, goes down to zero and then goes negative. In the two level model for β is related to the transition dipole moment squared, the change in the dipole moment and divided by the energy gap. Most aromatic molecules tend to be near polyene limit with a small β.
- <math>\beta \propto \left( \frac {\mu^{2} _{ge} ( \mu _ {ee} - \mu _{gg})} {E^{2}_{ge}}\right)\,\!</math>
Where:
- <math>\mu_{ge}\,\!</math> is the transition dipole moment
- <math>\mu_{ee}\,\!</math> is the dipole moment of the excited state
- <math>\mu_{gg}\,\!</math> is the dipole moment of the ground state
- <math>E_{ge}\,\!</math> is the energy gap between the states - or ωge the frequency corresponding to the excited state energy.
Considering only the two states the β model (blue circles) matches the experimental values (red dots) well. So the two state model looks good for β as well as α. The energy gap squared peaks at the cyanine limit as does the transition dipole moment.
A polyene that has no dipole moment (eg it is symmetrical) in the ground state will have no dipole moment in the excited state. The change in dipole moment (blue plus symbol) peaks closer to the polyene limit. Most aromatic molecules tend to be near polyene limit with a small beta. The beginning portion of the β curve looks almost linear, this led researchers to believe that they just had to add stronger donors and acceptors to the molecule in order to increase β. But they were not seeing the whole picture.
Factors Affecting Charge Separation
The relative contribution of each limiting resonance structure to the ground-state structure of a molecule is related to their relative energies. When the two resonance forms are very different in energy the ground-state structure will be dominated by the lower energy form and the molecules will exhibit a large degree of BLA.
In organic molecules there are two factors that dominate the energetics of the resonance structures to a first approximation.
First, there is a Coulombic term that is destabilizing when charge is separated. Adding donors and acceptors does encourage separation of charge but this also costs energy. Increasing the strength of the donor and acceptor end groups, and/or placing the molecule in a more polar solvent to the molecule can each lead to stabilization of the charge separated form.
In addition, there is also an energy consideration associated with the topology of the molecule. If a molecule has 6 π-electrons in a ring the molecule has an additional resonance stabilization and is referred to as aromatic. In the case of stilbene with added donor and acceptors there is a loss of aromaticity, (a loss of 36kcal/mol). This favors the molecule that is aromatic.
For molecules whose neutral forms are aromatic, charge separation will interrupt the aromaticity and yield structure with a higher energy quinoidal resonance form.
This disruption of the aromaticity results in additional destabilization due to the loss of aromatic stabilization and in such systems the molecule will be further biased towards the neutral resonance form
If, on the other hand, the neutral form is quinoidal, then the molecule will gain aromatic stabilization in the charge-separated resonance form. Aromaticity can be used as a driving force to get past the cyanine limit. The groups can used to tune the molecules for particular desired polarization characteristics.
Tuning Bond Length Alternation Leads to Optimization of β
We can tune aromaticity and charge separation.
Therefore we can tune energetics of resonance structures.
Therefore we can tune bond length alternation across a wide range.
If βis a peaked function, we can tune the bond length alternation so as to be at the peak and optimize β.
Evolution of Dipole Moments
Note that both the ground- and the excited-state dipole moments increase as BOA becomes more positive. However note also that the past the cyanine-limit (0 BOA) the excited-state dipole moment(μee) is less than the ground-state dipole moment(μgg) so Δ μ becomes negative. The excited state dipole moment vs BOA has a flat slope, while the groundstate dipole is going up, therefore the ground state is going to exhibit more polarizability.
Manipulation of BLA Through Topology
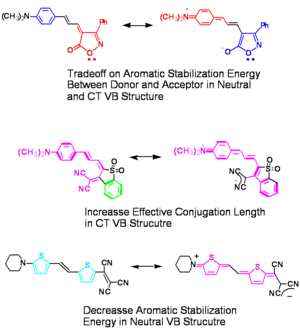
Until recently, most molecules that had been examined for NLO, such as donor-acceptor substituted stilbenes or diphenyl polyenes, had a very large BLA, typically greater than 0.10 Å. The calculations above, for example, predict that β is maximized at a value of ~0.04 Å; thus, these molecules with large BLA are not sufficiently polarized to give the correct BLA needed to maximize β. It was hypothesized that the high magnitude of BLA observed in the central polyene bridge of donor-acceptor substituted stilbenes and related molecules is indicative of an insufficient contribution of the charge-separated resonance forms to the ground-state configurations of the molecules and is a consequence of the loss of aromatic stabilization in the charge-separated forms.
We can tune aromaticity and charge separation. There first molecule is called an phenylisoxazimone. Aromatic groups must have 4n+2 electrons in a ring. The benzene has 4n+2. In the charge separated form there is a somewhat aromatic ring which offsets the loss of aromaticity from benzene.
In the second example there single bonds that are cross conjugated to a fully conjugated form when in the charge separated form.
In the third example of heterocycles such as thiophenes we start with neutral molecules that lack the full benzene aromaticity. You still lose aromaticity on both sides but not a full benzenes’ worth.
Using these techniques we can tune energetics of resonance structures therefore we can tune bond length alternation across a wide range. If β is a peaked function, we can tune the bond length alternation so as to be at the peak and optimize β.
References
- ↑ F. Meyers, S. R. Marder, B. M. Pierce, J. L. Bredas J. Am. Chem. Soc., 1994, 116 (23), pp 10703–10714 Electric Field Modulated Nonlinear Optical Properties of Donor-Acceptor Polyenes: Sum-Over-States Investigation of the Relationship between Molecular Polarizabilities (.alpha., .beta., and .gamma.) and Bond Length Alternation http://pubs.acs.org/doi/abs/10.1021/ja00102a040?journalCode=jacsat&quickLinkVolume=116&quickLinkPage=10703&volume=116
| Previous Topic | Return to Second-order Processes, Materials & Characterization Menu | Next Topic |