Lasers
| Previous Topic | Return to Optical Fibers, Waveguides, and Lasers Menu |
Lasers are a fundamental tool use in non linear optical research. The laser is both a research tool and a product of research. The evolution of tunable and high speed pulsed lasers has made it possible to study new phenomena and has created new technology with huge economic importance.
Emission and absorption of radiation
Laser is light amplification via stimulated emission of radiation. Stimulated emission is key to the ability of the process to amplify light. Mainman was the first person to develop the first visible laser using a ruby.
See Wikipedia:Laser
See Mainman 1960 [1]
See Cord Course on Lasers Lasers
Two state system
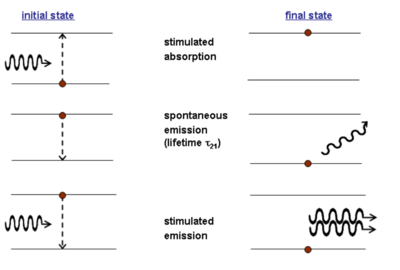
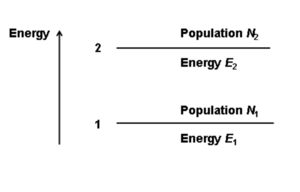
Consider a simple two level system. There are two population of molecules (N1 and N2) at two possible energy levels (E1, E2). An atom on level E1 can be elevated to E2.
The absorption of a photon with the correct energy hν (the difference between E1 and E2) results in a stimulated absorption and the system moves into the excited state. This leads to the emission of photon in a lifetime τ21. In spontaneous emission the emitted photon can have differing energies, polarization and phase than the stimulating photon.
In stimulated emission the absorbed photon causes the excited photon to emit light with specific characteristics.
The stimulating and stimulated photon have the same energy, same polarization, and the same phase. Emitted energy is perfectly coherent and the amplitude of the electric field can interfere completely constructively.
Einstein relations
When the system is in thermal equilibrium the rate of upward and downward transitions are equal (Einstein 1917). This is a dynamic equilibrium, there is still emission and absorption but the relative rates are equal.
upward transition rate
The upward transition rate is
- <math>N_1 \rho_\nu B_{12}\,\!</math>
where
- <math>N_1\,\!</math> is the atoms per unit volume with energy E1
- <math>\rho_\nu\,\!</math> is the energy density at frequency nu corresponding to the difference in energy between E1 and E2 (hν)
- <math>\rho_\nu = N_{\nu} h\nu \,\!</math>
Where Nν is the number of photons per unit volume having frequency ν
The coefficient B12 gives the probability of upward transition in a stimulated process.
stimulated emission rate
The stimulated transition rate from level 2 to level 1 is given:
- <math>N_2\rho_{\nu}B_{21}\,\!</math>
Where
- <math>N_2\,\!</math> is the number of atoms per unit volume in the collection with energy E2.
- <math>B_{21}\,\!</math> is the probability of the photons stimulating the downward transition.
The total downward transition rate is the sum of the induced and spontaneous contributions
- <math>N_2\rho_{\nu}B_{21} + N_2 A_{21}\,\!</math>
and
- <math>A_{21} = 1 /\tau_{21}\,\!</math>
The spontaneous term is only dependent on the population of the upper level, it is not affected by the photons, and by the lifetime of the excitation on level 2 going to level 1.
The Einstein coefficients A21 B21 and B12 are dependent on the material. For a system in thermal equilibrium the upward and downward transition rates must be equal.
- <math>N_1 \rho_\nu B_{12} = N_2 \rho_\nu B_{21} + N_2 A_{21}\,\!</math>
Rearranging the equation in order to get the expression in terms of energy density.
- <math>
N_1 \rho_\nu B_{12} = N_2 \rho_\nu B_{21} + N_2 A_{21}\,\!</math>
We move :<math>\rho_\nu\,\!</math> to the left:
- <math>\rho\nu = \frac {N_2A_{21}} { N_1B_{12} – N_2B_{21}}\,\!</math>
Then divide the right side numerator and denominator by N2:
- <math>\rho_\nu = \frac {A_{21}/B_{21}} {[(B_{12}/B_{21}) (N_1 N_2)] -1}\,\!</math>
The ratio of the stimulated absorption emission coefficients times the ratio of the populations goes to one.
Bolztman Statistics
We can express N1 and N2 the ratio of the populations at thermal equilibrium using Botzmann statistics :
- <math>N_j = N_o \frac {g_j exp (-E_j/kT)} {\sum {g_i exp(-E_i/kT)}}\,\!</math>
- <math>N_j\,\!</math> is the population density of energy level Ej
- <math>N_o\,\!</math> is the total population density
- <math>g_j\,\!</math> is the degeneracy of the jth level (g terms go to 1 if there no degeneracy).
- <math>E_j\,\!</math> is the energy of the jth level
The denominator is the sum across all possible levels i. If we consider N1/N2 we only need the numerator because the term corresponding to the summation cancels out.
This gives:
- <math>\frac {N_1} {N_2} = \frac {g_1}{ g_2} exp [(E_2-E_1)/kt]= \frac {g_1} {g_2} exp(h\nu/kT)\,\!</math>
Then plug it into the previous expression
- <math>\rho_\nu = \frac {A_{21}/B_{21}} {[(g_1/g_2) (B_{12}/B_{21}) exp (h\nu /kT)] -1} \,\!</math>
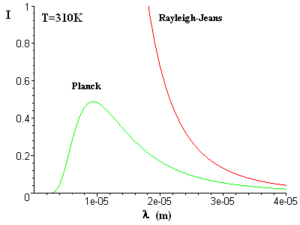
Since the collection of atoms in the system is in thermal equilibrium the radiation is blackbody radiation. Blackbody radiation or “cavity radiation” refers to an object or system which absorbs all radiation incident upon it and reradiates energy which is characteristic of the radiating system only, and is not dependent on the type of radiation that is incident on it. The sun can be considered a blackbody. The radiated energy can be considered to be produced by standing wave or resonant modes of the cavity which is radiating.
See GSU hyperphysics on http://hyperphysics.phy-astr.gsu.edu/hbase/mod6.html
Classical versus quantum model
The cavity absorbs all radiation incident upon it leading to radiation. The more the number of modes the higher the energy. In a classical description the amount of radiation should be proportional to the number of modes at a given frequency with the probability of modes per unit frequency per unit volume is equal. The average energy of emission is only dependent on the kT and thus the energy should increase indefinitely with temperature. This is true in the lower energy range but deviates significantly at shorter wavelengths. This was referred to the “ultraviolet catastrophe” because at higher energies there is a lower probability of finding the correct mode.
| #Modes /unit frequency, volume | Probability of occupying modes | Average energy per mode | |
|---|---|---|---|
| Classical | :<math>\frac {8\pi \nu^2 } {c^3}\,\!</math> | Equal for all modes | <math>kT\,\!</math> |
| Quantum | <math>\frac {8\pi \nu^2 } {c^3}\,\!</math> | Quantized, hν required, upper modes less probable | <math>\frac {h\nu} {exp(h\nu/kT) -1}\,\!</math> |
Quantum mechanics was able to explain this. The number modes is the same in classical and quantum physics varies as the square of the frequency. But in quantum physics the average energy is quantized by hnu and the probability of reaching the exact required state for a given wavelength changes exponentially at higher energy levels.
The blackbody radiation density is
- <math>\rho_\nu = \frac {8\pi h\nu^3 n^3} {c^3} \left( \frac {1} {exp(h\nu/kT) -1} \right)\,\!</math>
Where
- <math>n\,\!</math> is the refractive index of the medium
The prefactor depends on the cube of the frequency, and the cube of the speed of light in a vacuum. Now we can compare to expressions for :<math>\rho_\nu\,\!</math>
- <math>\rho_\nu = \frac {a_{21}/B_{21}} [(g_1/g_2) {(B_{12}/B_{21})exp(h\nu /kT)]-1}\,\!</math>
and
- <math>\rho_\nu = \frac {8\pi h\nu^3 n^3} {c^3} \left( \frac {1} {exp(h\nu/kT) -1} \right)\,\!</math>
Einstein relations:
If we eliminate the degeneracy factor the oscillator strength for going from the ground state to the excited state is the same as that going from the excited state back down.
- <math>g_1B_{12} = g_2B_{21}\,\!</math>
Which leads to the ratio of the Einstein coefficients for spontaneous and stimulated emissions equal to:
- <math>\frac {A_{21}} {B_{21}} = \frac {8\pi h \nu^3 n^3} {c^3}\,\!</math>
The ratio of R of the rate of spontaneous absorption to the rate of stimulated emission for a given pair of energy levels.
- <math>R = \frac {A_{21}}{ \rho_\nu B_{21}}\,\!</math>
Spontaneous emission (A21) does not depend on energy density but stimulated emission does.
- <math>R = exp(h\nu/kT)-1\,\!</math>
Thus for emission in the middle of the visible spectrum (2.5 eV) at room temperature kT is relatively large, e100 -1 is very small. Thus a thermal equilibrium stimulated emission is not an important process.
The goal is to increase stimulated emission because this light is completely coherent allowing extremely high intensities.
For a given pair of energy levels:
Stimulated emission is described
- <math>N_2\rho_\nu B_{21}\,\!</math>
- We must increase both the radiation density (rhonu) and the population density N2 of the upper level in relation to the population density, and for a given material B21 is fixed.
- We must create a condition in which N2>(g2/g1) N1 even though E2>E1
This requires a population inversion in which the higher level is more populated than the lower level. Mainman did this with ruby laser but it was very difficult because the lower energy level was the ground state which is heavily populated. Other lasers have been developed where the energy transition is between two excited states. Thus it is much easier to have a inversion of population.
Absorption of radiation
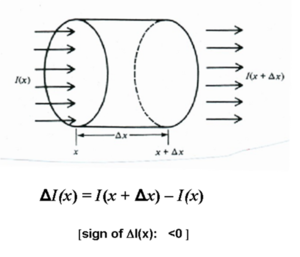
Consider a collimated beam of perfectly monochromatic radiation of unit cross-sectional area passing through an absorbing medium. Also assume for simplicity that it is a two level system with transition between E1 and E2.
As the beam with irradiance I(x) enters the medium at x and moves to position Delta x
- <math>\Delta I(x) = I (x + \Delta x) – I(x)\,\!</math>
( the sign of Δ I(x) is negative because it is an absorbing medium)
The beer lambert law states that for a homogeneous medium:
- <math>\Delta I(x) = - \alpha I(x) \Delta X\,\!</math>
Where:
Alpha is the absorption coefficient which is positive
- <math>\frac {dI(x)} {dx} = -\alpha I(x)\,\!</math>
If we integrate:
- <math>I= I_o exp(-\alpha x)\,\!</math>
Where
- <math>I_0\,\!</math> is the incident irradiance
- <math>x\,\!</math> is the length of the path through the medium
The net rate of loss of photons per unit volume from the beam as it moves through a volume element of medium of thickness Delta X and unit cross-sectional area is given by:
- <math>- \frac {dN_\nu} {dt} = N_1 \rho_\nu B_{12} – N_2 \rho_\nu B_{21}\,\!</math>
Where
- <math>N_1 \rho_\nu B_{12}\,\!</math> is the rate of absorption
- <math>N_2 \rho_\nu B_{21}\,\!</math> is the rate of emission
Ignoring the degeneracy factors B21 equals B12. The rate of emission is dependent on the population of the two levels.
- <math>-\frac {dN_\nu} {dt} = (\frac {g_2}{g_1} N_1 - N_2) \rho_\nu B_{21}\,\!</math>
If we ignore photons created by spontaneous emission and scattering losses.
The irradiance is the energy cross a unit area per unit time, which is the energy density times the speed of light in the medium.
Using dimensional analysis:
Energy crossing an area in a unit time has units J/m2 t which is equivalent to energy density J /m3 times the speed of light in m/s
For photons of frequency nu:
- <math>I_\nu = \frac {\rho_\nu c}{n} = \frac {N_\nu h\nu c}{n} ; N_\nu = \frac {I_\nu n}{[h\nu c]}\,\!</math>
Where
- <math>I_\nu\,\!</math> is the irradiance at frequency nu
- <math>n\,\!</math> is the refractive index of the material
- <math>\nu\,\!</math> is frequency that can excite from the ground to the excited state
- <math>N_nu\,\!</math> is the energy density
The more that light is slowed down within the medium the more time there is for absorption.
The photon density decreases as it passes through a distance Δ x of f the volume element according to:
- <math>-dN_\nu(x)= [I_\nu (x) – I_\nu (x + \Delta x] \frac {n} {h\nu_{21}c}\,\!</math>
If Δx is sufficiently small you can integrate:
- <math>-dN_\nu(x) = - \frac {dI_\nu(x)} {dx} \cdot \frac {\Delta x n} {h\nu_{21}c}\,\!</math>
and
- <math>(\Delta x n/c = \Delta t)\,\!</math>
This implies that the rate of decay of photon density in a time interval dt:
- <math>\frac {dN_\nu} {dt} = \frac {dI_\nu(x)} {dx} \cdot \frac {1} {h\nu_{21}}\,\!</math>
- <math>\frac {dN_\nu} {dt} = -\alpha I_\nu (x) \cdot \frac {1} {h\nu_{21}} = -\alpha \rho_\nu \frac {c}{n} \cdot \frac {1} {h\nu_{21}}\,\!</math>
where
- <math>-\alpha I_\nu(x)\,\!</math> is the variation of the irradiance by unit volume
We can build a rate of disappearance of photon density as a function of absorption coefficient and the expression of photon density as a function of populations.
- <math>\alpha \rho_\nu \frac {c}{n} \frac {1}{h \nu_{21}} = \left (\frac {g_2}{g_1} N_1-N_2 \right) \rho_\nu B_{21}\,\!</math>
And finally put it all in terms of alpha:
- <math>\alpha = \left( \frac {g_2}{g_1} N_1 – N_2 \right) \frac {B_{21} h\nu_{21} n} {c}\,\!</math>
Thus the absorption coefficient alpha depends on the difference in the population difference between levels E1 and E2.
For a collection of atoms in thermal equilibrium since E2>E1 then:
- <math>(g_2/g_1) N_1 > N_2\,\!</math>
Hence α is positive and normally N2 is very small. But if we can create a situation for which:
- <math>(g_2/g_1) N_1 < N_2\,\!</math>
That is if there is an inversion of population, then α becomes negative.
If the beam is right energy hν and the excited state population is larger than the ground state, then the probability of a stimulated emission from the excited state is higher than the probability of a stimulated absorption from the ground state.
In this case the irradiance of the beam grows as it propagates through the medium.
Recalling that: I = I0exp(-αx) we obtain an exponential relationship:
- <math>I = I_0 exp(kx)\,\!</math>
- <math>k\,\!</math> is referred to the small signal gain coefficient or simply gain coefficient
- <math>k =(N_2- \frac {g_2}{g_1} N_1) B_{21} \frac {h\nu_{21}n} {c}\,\!</math>
Population Inversion
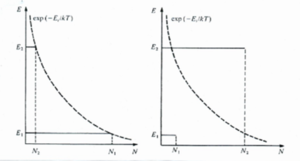
The plots show the energy of the two states (E2, E1 - y axis) and the population of each excited state (N2, N1 - x axis). The dotted line is the exp(-Eν/kt) thermal equilibrium distribution.
In the two level system at thermal equilibrium N2 is always smaller than N1. In order to reach a population inversion one has to pump the system into the excited state. Light or electrical current can be used to pump a system as in a diode laser. In the pumped condition the N1 population is far smaller than the boltzman distribution while the N2 population is far greater.
The ratio of the population in thermal equilibrium is given by boltzman statistics:
- <math>\frac {N_1} {N_2} = \frac {g_1} {g_2} exp [(E_2-E_1)/kt]= \frac {g_1}{g_2} exp(h\nu/kT)\,\!</math>
If hν ~ 2.5 eV (visible part of spectrum) and g2 =g1 at room temperature (kT = .025 eV)
- <math>N_2/N_1 = exp (-h\nu/kt)\,\!</math> ~ e-100 ~ 10-43 (10 ~ e2.3 so to make a conversion divide e exponent (that is 100) by 2.3)
This is a very small ratio.
Example If we consider an octamer of phenylene vinylene which absorbes around 2.5 eV (= E2-E1). Assume the molar mass is ~ 1000g and the density is 1 g per cm3
What is roughly the length of the side of a cube containing oligophenylene vinylene in which on average one molecule will be be in the excited state at room temperature?
Answer You would need 1043 molecules which weighs 1.6 x 1023 grams which take up 1023 cm3 or a cube that is 1017 m3 that is 108 km3 which is a cube 464 km on a side.
In order to get an population inversion we must supply a large amount of energy to excite atoms into the upper E2. Since B12 and B21 are equal (assuming g1 = g2). Once atoms are excited into the upper level the probabilities of further stimulated absorption or emission are equal. The best that can be achieved with a two level system is equality of the populations of the two levels. Thus you can not get to the state of inverted population. This is the reason to consider a three level system.
3 Level System
The idea of three level system was proposed by Bloembergen in 1957 and received a Nobel prize in physics in 1981 for his work with nonlinear optics and lasers. He currently has a position at the University of Arizona optical science center.
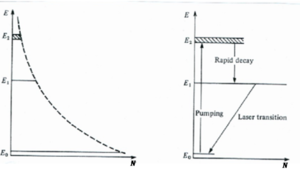
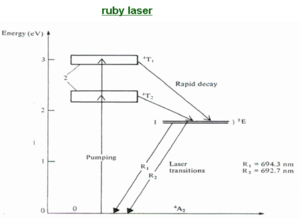
In the three level system E2 is a second excited state. If atoms are intensely illuminated electrons can be pumped into E2 from the ground state E0. From E2 the electrons decay by non-radiative processes to level E1 so that a population inversion may be created between E1 and E0. Transition from level E2 to E1 should be very rapid thereby ensuring that there are always vacant states at E2. Transition from E1 to E0 should be very slow; E1 has to be metastable state so that you can accumulate a population.
Level E2 should preferably consist of a large number of closely spaced levels so that pumping uses as wide a part of the spectral range of the pumping radiation as possible.
Three level lasers such as ruby require a very high pump power because the terminal level of the laser transition is the ground state.
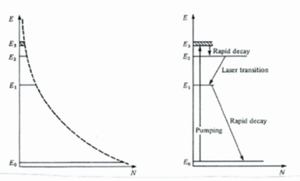
4 level system
In a 4 level system there is population inversion between two excited state (E2 and E1). Pumping puts electron directly into a series of levels at E3. Internal conversion brings the electrons rapidly down to a metastable E2 where they accumulate and the population is inverted with respect to E1. E2 to E1 is a radiative transfer. From E1 top E0 there should be rapid decay so that the level is replenished for pumping. Even with pumping the population of E1, E2 and E3 is less than that of E0.
The frequency of light used for pumping must be correct for jumping between E0 and E3. The laser light produced reflects the transition between E2 and E1.
Most scientific lasers are solid state. They have a host materials (such as ruby or YAG) with dopants (niodinium) that have the lasing transitions.
In the Nd-YAG laser
- T32 ~ 10-8s
- T21~ .5 ms
- T10~ 30 ns
Much of laser research is the search for lasing host materials with energy transitions and time characteristics that are favorable to generating the right balance when pumped.
Optical Feedback
Positive feedback may be obtained by placing gain medium between a pair of mirrors which form a optical cavity. (a Fabry-Perot resonator) This allows the beam to make repeated passes through the medium gaining energy with each pass due to stimulated emission. A semitransparent mirror on one end finally allows the beam to escape when it has reached sufficient intensity. There are many systems that provide amplification of the signal and there are conjugated polymers that allow amplified stimulated emission. But that is not the same as laser. Three groups discovered lasing in conjugated polymers in the mid 1990s, Allan Heeger at Santa Barbara, Richard Friend at Cambridge, and Z.V. Vardeny at University of Utah. Since then there have been many efforts to create a diode laser from a conjugated polymer, but without success.
The problem is that you need to build a large population in the excited state. In an LED electrons are injected from ones side and holes are injected from the other and when they combine there must be large densities in the excited state. However the presence of injected charge (polarons) quenches the exciton. You don’t have that issue with optical pumping because you start with nothing, the atoms absorbs light and directly build up the population in the excited state. There are no polarons or charges floating around.
Laser Modes
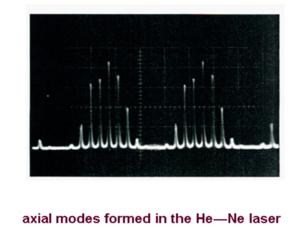
Axial Modes
The two mirrors of the laser form a resonant cavity and standing wave patterns are set up between the mirrors. Standing waves satisfy the condition:
- <math>p \frac {\lambda} {2} = L\,\!</math>
- <math>L\,\!</math> is the optical path between the mirrors (which is a product of the physical length and the index of refraction).
- <math>p\,\!</math> is an integer
The length of cavity needs to be and integral multiple of half the wavelength in order for each reflection to be coherent with the preceding waves.
Substituting for wavelength for c/ν :
- <math>\nu = \frac{ pc}{2L}\,\!</math>
There are many values of for p that will satisfy this equation.
Example
If L = .5m and λ ~500 nm, then there are 2 x 106 possible p values.
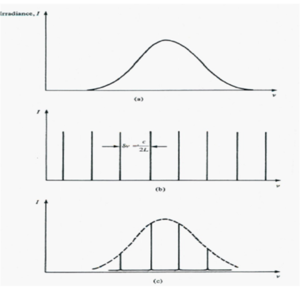
Each value of p satisfying the above equations defines an axial (or longitudinal) mode of the cavity. The frequency separation (Δ p =1) is given by:
- <math>\Delta \nu = \frac {c}{2L}\,\!</math>
For L= .5m Δ ν = 300 Mhz, this corresponds to an photon energy difference of 10-6 eV(1eV ~ 2 x 1014 hz)
Thus the modes of oscillation of the laser cavity consist of a large number of frequencies separated by c/2L. Specific frequencies are able to stimulate additional photons of the same wavelengths (when the beam goes back and forth in a resonating cavity). This results in a distribution of photons that are separated in energy by 300 mhz or a millionth of an eV.
The envelope corresponds to a number of photons with very precise energy.
Transverse modes
Up to this point we have been discussing only the axial or longitudinal axis in which waves travel along a line joining the centers of the mirrors. For any real laser cavity there will be waves travelling just off the axis that are able to replicate themselves after covering a closed path. It is possible to have beams that are reflected at different angles. These transverse electromagnetic fields also give rise to resonant transverse electromagnetic modes (TEM) but the because they have components of their electromagnetic field that is transverse to the direction of propagation. The TEM subscripts indicate the number of modes along the x and y axis and you can see these patterns from lasers producing these modes.
Classes of Lasers
Doped insulator lasers
These are lasers whose active medium consists of a crystalline or amorphous (glassy) host material containing active ions, typically from the transition metal and rare earth groups in the periodic table.
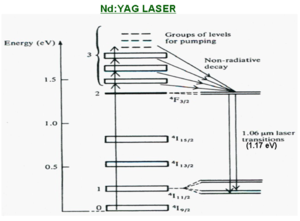
Nd:YAG laser.
This is a common laser used in research. When you see the wavelength reported in research as 1.064 micron this indicates that a Nd:YAG laser was used. Similarly a wavelength 532 nm this means they used a Nd:YAG but cut the wavelength in half using a nonlinear process.
The active material is yttrium aluminum garnet (Y3Al5 O12) is a garnet in which the aluminum oxide in garnet is replaced by ytrium in an orderly fashion. It has the rare earth metal ion neodymium Nd3+ present as an impurity. Nd3+ ions are randomly distrubuted as substitutions on lattice sites normally occupied by Y3+ ions. The Nd3+ provide the energy levels for both the lasing transitions and pumping.
These are the transitions within the neodymium ion. There are three levels in E3 which can be pumped into and which all undergo fast nonradiative decay into the E2 state. The laser transition happens between E2 and E1 with a 1.05 Um wavelength (in the near IR). From N1 there is a rapid non-radiative decay to the groundstate N0. The lifetime of the lasing transition is long which is what allows it to build up the population in E2 for population inversion. It is important to be aware of the relative energy levels and the speed of various transition that makes each the laser system work.
Pumping is normally achieved using an intense flash of white light from a xenon flashtube. The presence of several possible pumping transition E3 levels contributes to the efficiency of the laser when using a pumping source with a broad spectral output. Each level is able to capture a slight different part of the pump light spectrum.
Ruby laser
Ruby was the first visible laser that was developed. The active materials is a synthetically grown crystal of ruby, that is aluminum oxide with about 0.05% by weight of chromium as an impurity. Most precious gems have impurities in a very common material. The ruby has transitions at the upper end of the visible spectrum in the green and violet (2-3 eV) which is what gives the ruby its characteristic deep red color.
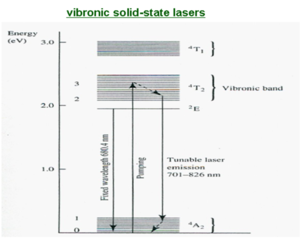
Vibronic laser
Vibronic laser such as a alexandrite and Ti-sapphire are similar to other solid state lasers such as Nd:YAG in that light from a external pump source excites the impurity ions in a transparent host. The sapphire laser is similar to the ruby, it is aluminum oxide with impurities such as titanium.
They are fundamentally different in that laser gain is possible over a broad range of wavelengths so that they can produce either tunable outputs or ultrashort pulses.
Vibronic laser such as a alexandrite and Ti-sapphire are similar to other solid state lasers such as Nd:YAG in that light from a external pump source excites the impurity ions in a transparent host. The sapphire laser is similar to the ruby, it is aluminum oxide with impurities such as titanium.
They are fundamentally different in that laser gain is possible over a broad range of wavelengths so that they can produce either tunable outputs or ultrashort pulses.
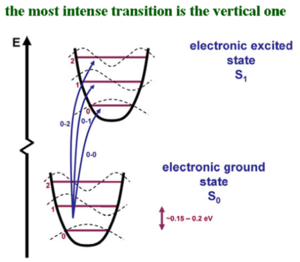
Vibronic solid state lasers have four level systems. The pumping radiations excites the active ions to a vibronic band. The ions then lose vibrational energy and drop to the bottom of the band which is the upper laser level. The laser transition then occurs to a vibrationally excited sublevel of the n1 state; this is followed by the ions relaxing to the lowest sublevel of the ground state.
Alexandrite laser comprises Cr3+ ions in a beryllium aluminate (BeAl2O4) host.
The pumping leads from the lowest vibration level of the ground state to a high vibrational level of E3, followed by relaxation to the zeroth level of the excited state E3. Then the excited emission (laser) occurs between some level in E2 and some vibrational level of E1. This gives a wide range of combinations of energy transitions that make it possible to tune the laser by filtering what comes out of the laser. This gives a range of 701 to 826 nm. The broad energy range of emission means that the time of the emission can be very short. Ti-sapphire is the most used laser for femptosecond pulse studies.
The Heisenberg uncertainty principle tells us that if the precision on energy is high the precision on time will be low. Femptosecond pulses will have energy scattered over 1.5 eV. When doing spectroscopy where accuracy in energy domain (milli- eV precision) is important then it is better to use longer pulses in the picoseconds.
Semiconductor lasers
Semiconductor lasers such as the diode laser are made with p-n junctions. It users an LED with a very high density of emission.
Gas lasers
Gas lasers are the most widely used type lasers. The helium laser is used for the red laser pointer, or the CO2 laser used in medicine. Basically there are three classes of gas lasers according to whether the transitions are Between electronic energy levels of atoms or Between electronic energy energy of ions or Between the vibrational/ rotational levels of molecules.
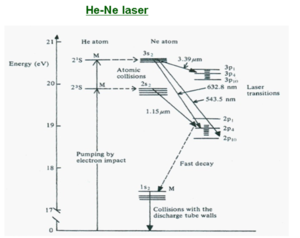
Atomic laser – the HE-NE laser The active medium is a mixture of 10 parts helium to one part neon. Neon provides the energy levels for the laser transition. Helium provide an efficient excitation mechanism for the neon atoms. Excitation usually takes place in a DC discharge created by applying a high voltage ( ~2-4 kV) across the gas. This creates high energy electrons in the gas mixture. The electrons hit the helium atoms (which are most common) bringing them to the excited state, and then transfer energy to the neon atoms when the energy of the excited states match. The neon can then relax to laser transitions levels such 3s level to 3p levels and then 3p to 2s and 2p levels.
- <math>E1 + He = He* +e2\,\!</math>
Resonant transfer of energy is proportional to exp (-ΔE/kt) where ΔE is the energy difference between the excited states of the two atoms involved.
- <math>He* + Ne = Ne* +He\,\!</math>
Liquid Dye lasers
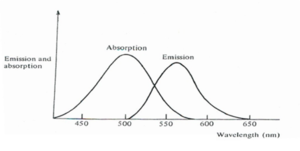
Liquids have useful advantages over solids and gases. Solids are very difficult to prepare with the requisite degree of optical homogeneity and they suffer permanent damage if overheated. Gases do not have these difficulties but they have a much smaller density of active atoms. The dye laser has the advantage that they are simple and they can be tuned over a significant wavelength range.
The active medium is an organic dye dissolved in a solvent. It is a four level system that uses piconjugated chromophores. The pumping makes the dyes go from the electronic groundstate to an excited vibrational level of an excited state. The E3 level is the top vibronic level of the excited state curve, relaxation occurs down to the bottom of the E2 level. Laser emission can occur from all the vibronic levels.
The broad range of emission can be filtered for specific wavelengths.
Rhodamine is a common laser dye with a cyanine type structure. It is dissolved in methanol. It has as broad tuning range (570-660 nm) All dye lasers are optically pumped.
See Cord Module on Dye lasers Dye lasers
References
- ↑ T.H. Mainman, Nature 187, 493 (1960) doi:10.1038/187493a0
| Previous Topic | Return to Optical Fibers, Waveguides, and Lasers Menu |