Bloch's Theorem
| Previous Topic | Return to Band Structure Menu | Next Topic |
As polyenes get longer and longer one could calculate and combine the wave functions for all the bonds, but this is not very efficient. Instead it is more powerful to consider the periodicity of repeated units. This is the purpose of Bloch's Theorem.
Bloch’s Theorem
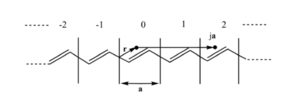
Consider the repeat unit cell (with cell length a) and the interactions with its neighbors. For example if you move over 2a units from point r you should find the same electron density at that point ja as point r. Because of the translation symmetry electron density at point <math>\overrightarrow{r}\,\!</math> in cell j (j equiv integer) must equal the electron density at point <math>\overrightarrow{r}\,\!</math> in the origin cell.
Bloch' Theoem:
- <math>\vert \Psi (\overrightarrow{r} + j \overrightarrow{a}) \vert^2 = \vert \Psi (\overrightarrow{r} ) \vert ^2\,\!</math>
- <math>\downarrow\,\!</math>
- <math>\Psi (\overrightarrow{r} + j\overrightarrow{a}) = exp (i \overrightarrow{k}j\overrightarrow{A}) \Psi (\overrightarrow{r})\,\!</math>
where:
- <math>exp (i \overrightarrow{k}j\overrightarrow{a})\,\!</math> is the phase factor
The square of the wave function at r plus ja is the same as square of the wave function at r.
Phase Factor
The phase factor takes into account that there has been a translation.
The phase factor can be calculated using algebraic substitutions:
- <math>exp (i \overrightarrow{k}j\overrightarrow{a})= cos(\overrightarrow{k}j\overrightarrow{a})+i sin(\overrightarrow{k}j\overrightarrow{a})\,\!</math>
- <math>\vert exp(i \overrightarrow{k}j\overrightarrow{a})\vert ^2 = exp (i \overrightarrow{k}j\overrightarrow{a}) exp(-\overrightarrow{k}j\overrightarrow{a})\,\!</math>
- <math>=(cos(\overrightarrow{k}j\overrightarrow{a}))^2 +(sin(\overrightarrow{k}j\overrightarrow{a}))^2\,\!</math>
- <math>=1\,\!</math>
where:
- <math>\overrightarrow{k}j\overrightarrow{a} \equiv\,\!</math> argument of an exponential (no dimensions)
- <math>\overrightarrow{a} \equiv\,\!</math> length of a unit cell in direct space
- <math>\overrightarrow{k} \equiv \frac {1} {length}\,\!</math> defined in reciprocal space
The phase factor accounts for the translation in the original equation. The argument of an exponential has to be dimensionless. If there is a term like a which is a length, then there must be a term k that is 1/length in order to remove dimensions from the equation. A is measured in direct space that is a measure of the length of the unit cell, k is defined in reciprocal space.
Any kind of mathematical analysis that involves periodic structures (x-ray diffraction or neutron diffraction) in three dimensions will have some form of a phase factor. As a convention the phase factor is written (ikja).
The same kind of analysis can found in X-ray structure determination of crystals. They use this convention for phase factor:
- <math>exp(i 2 \pi \overrightarrow{k} j \overrightarrow{a})\,\!</math>
This doesn’t change things because the 2π simply returns you to the same point on the imaginary and real axes plot.
Electron Momentum and Wavelength
- <math>\overrightarrow{k}\,\!</math> is a wavevector of the electron, that is related to the wavelength of the electron.
Any object has an associated wavelength that is given by:
- <math>\overrightarrow{k}= \frac{ 2\pi} {\overrightarrow{\lambda}}\,\!</math>
- <math>\overrightarrow{\lambda} \equiv electron \, wavelength \equiv \frac {h} {m\overrightarrow{v}}\,\!</math>
- <math>\hbar \overrightarrow{k}\equiv electron \, momentum\,\!</math>
- <math>\hbar (\equiv \frac {h} {2\pi} )\,\!</math>
Where
- <math>\mu\,\!</math> is plank’s constant
- m is mass
- v is velocity
when
- <math>\overrightarrow{k}= 0 \Rightarrow \overrightarrow{\lambda} = \infty\,\!</math>
- <math>\overrightarrow{k}= \frac {2\pi} {\overrightarrow{a}} \Rightarrow \overrightarrow{\lambda} = \overrightarrow{a}\,\!</math>
- <math>\frac {2\pi} {\overrightarrow{a}}\,\!</math> is the unit-cell in reciprocal space
In x-ray diffraction convention the unit cell would be
K is directly related to the wavelength of the electron and can have any value. :<math>\frac {1} {\overrightarrow{a}}\,\!</math>
Example: What is the human wavelength?
Mass times velocity is the momentum.
A person moving has a very large mass compared to that of an electron. Using the equation a person’s wavelength would be 10-25 Å.
But in the range of a the electron mass of 10-27 this leads to electron wavelengths in the range of Å which is measureable.
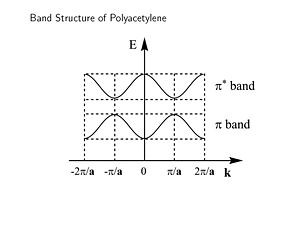
Band Structure of Polyacetylene
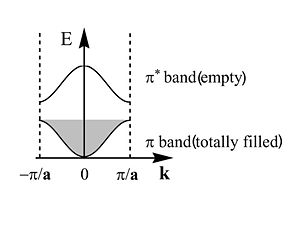
This is band structure of polyacetylene derived using Bloch’s Theorem. It is a plot of energy versus wavevector of the electron. This makes sense since the wavevector is related to the momentum and therefore energy of the electron. The periodic behavior will continue across the length of the chain. The energy of the π an π* bands are symmetrical and inverted. There is periodicity in both direct and reciprocal space.
The zone from <math>-\frac {\pi} {\overrightarrow{a}}\,\!</math> to <math>+\frac {\pi} {\overrightarrow{a}}\,\!</math> is called the first Brillouin zone of the polymer. The whole information about a periodic molecule is contained between 0 and π/a (the first half of the Brillouin Zone, since the
<math>E(\overrightarrow{k})\,\!</math> curves are periodic (periodicity <math>2\pi/\overrightarrow{a})\,\!</math>
and
<math>E(\overrightarrow{k}) = E(-\overrightarrow{k})\,\!</math> ).
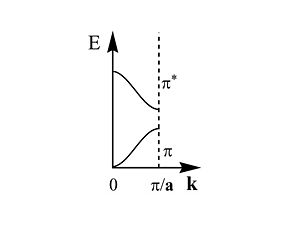
The first half of the Brillouin zone is located 0 and <math> \frac {\pi} {\overrightarrow{a}}\,\!</math>. In a three dimensional system the only difference is that the unit cell has a,b and c components, and in reciprocal space a corresponding set of reciprocal values. As we move from the center of the Brillouin zone (0) to the edge of the Brillouin zone (π/a) the π band goes up in energy while the π* band goes down.
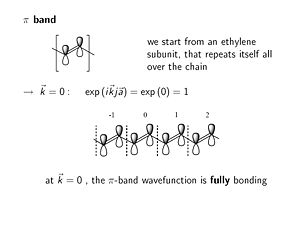
π Band
The π band within the unit cell behaves like an isolated ethylene subunit. The π level is bonding and the π* level is antibonding.
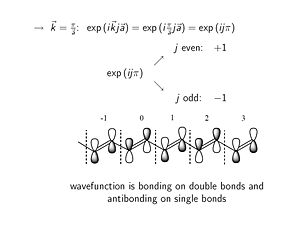
- <math>\rightarrow \overrightarrow{k} = 0 : exp (i \overrightarrow{k}j \overrightarrow{a}) = exp(0) = 1\,\!</math>
At k = 0 the phase factor is exp(0) which is 1. At K equals zero the imaginary component goes away, the cos(0)=1. When you look at the wave function in any other unit cell with respect to the origin unit cell you multiply by the phase factor =1; this results in the same fully bonding wave function all along the molecule.
Consider what happens approaching the edge of the Brillouin zone (k= π/a).
- <math>\rightarrow \overrightarrow{k} = \frac {\pi} {\overrightarrow{a}} : exp (i \overrightarrow{k}j \overrightarrow{a}) = exp(i \frac {\pi} {\overrightarrow{a}}j \overrightarrow{a}) = exp(i j \pi)\,\!</math>
In case of an even unit cell number of J the phase factor is +1, while for odd numbered unit cells there a phase factor of -1. A -1 phase factor times the original wave function flips the orientation of the bonding orbital. At the single bonds (π/a) there are nodes where energy is zero. The top of valence band at k=π/a has a wave function which for a long molecule constututes the HOMO level of the molecule. There bonding factors where in the ground state there are double bonds, and antibonding factors where in the ground state there are single bonds.
π* Band
Consider the π* band for the ethylene subunit.
At <math>\overrightarrow{k}=0\,\!</math> the phase factor is 1 everywhere. This is the fully antibonding case which has the maximum number of nodes, one node in the middle of each bond along the chain.
At <math>\overrightarrow{k}=\frac {\pi} {\overrightarrow{a}}\,\!</math> there is an antibonding situation within the unit cell but a bonding situation between unit cells. The LUMO bonding and antibonding is exactly opposite of that of the HOMO. So there is antibonding where there is a double-like bond factor, and bonding where there is a single-like ground state bond factor.
Band Gap
The π band goes up in energy from <math>\overrightarrow{k}=0\,\!</math> to <math>\overrightarrow{k}=\frac {\pi} {\overrightarrow{a}}\,\!</math>
The π* band goes down in energy from <math>\overrightarrow{k}=0\,\!</math> to <math>\overrightarrow{k}=\frac {\pi} {\overrightarrow{a}}\,\!</math>
The π and π* bands have the same wave function characteristics as the HOMO an LUMO levels of the small polyenes.
The bandgap ( here Eg~1.5eV) is said to be a direct bandgap at <math>\overrightarrow{k}=\frac {\pi} {\overrightarrow{a}}\,\!</math>
- <math>\vec{k} = \frac {2\pi}{\vec{\lambda}}\,\!</math>
When :<math>\vec{k}=0\,\!</math> the wavelength is infinite
When :<math>\vec{k}=\pi/a\,\!</math> the wavelength is 2a
It is possible to connect the electronic properties of periodic systems and molecular orbitals of simple molecules like butadiene.
At absolute zero temperature the π band is completely filled with electrons. Any electron with momentum of +k will have a corresponding electron with –k, so the net momentum of all the electrons is zero, so there is no net displacement of charge, so there is no current. In order to have a current there has to be electrons getting into the empty band, so that when there an applied field you can have a net displacement of charges in one direction. This is why the π* band is called the conduction band. Electrons have to jump into the conduction band for there to be current. This is considered an intrinsic system, with no input and outputs. Dopants can make the system conductive so that when electrons are externally added or removed there will be conduction.
| Previous Topic | Return to Band Structure Menu | Next Topic |