Propagation, Reflection and Refraction

Previous Topic

Return to Basics of Light Menu

Next Topic

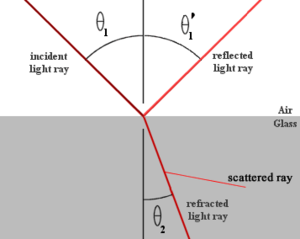
When light hits a material it can be refracted, reflected or absorbed.

Error creating thumbnail: Unable to save thumbnail to destination

The speed of light changes slightly as it passes into a new medium. This results in a bending of light in order to maintain a constant frequency.

Reflection

Reflection, refraction, and scattering compared

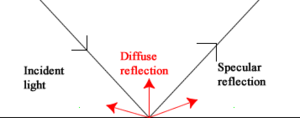
Light will be reflected symmetrically. In a perfectly smooth specular (from the latin speculum- meaning mirror) surface the angle of incidence is equal to the angle of reflection. If you have rough surface light will be reflect in all directions causing diffuse reflection.

Diffuse and specular reflection

Refraction

When light penetrates into a material it slows down.The amount it slows down depends on the index of refraction.

<math>v_m = \frac{ c} {n_m}\,\!</math>

where:

<math>n_m\,\!</math> is the index of refraction of the medium

<math>n_m \equiv f(\lambda)\,\!</math>

Index of refraction varies with frequency. This is because light has an electronic field that interacts with the electrons and positive charges in the material. Physics and chemistry are 99.9% electrostatics.

Light can be refracted when it penetrates into a medium. For example, when you put your arm into a bucket of water it appears to be bent. Light slows down when it passes through different media and is bent.

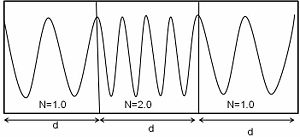
<math>\lambda_0 \rightarrow \frac {\lambda_0} {n_m} = \lambda_m\,\!</math>

<math>\lambda_m < \lambda_0\,\!</math>

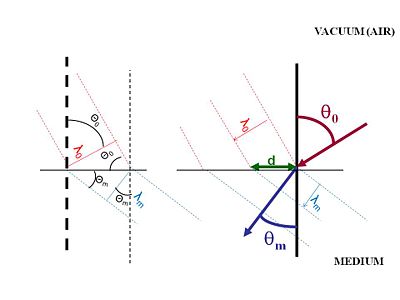
Air has a refractive index that is close to 1.The illustration shows light approaching a surface with a wavelength <math>\lambda_0\,\!</math> measured as the distance between wave crests. When light passes from air into another medium there is distance between wave crests as they enter the medium identified as d. At the surface the distance d must be the same for the incident beam and the diffracted beam. When the light enters the new materials light is slowed down while the frequency stays the same, this means that the diffracted beam must have a smaller wavelength.

The horizontal line represents the interface between two materials. The red arrow is the incident light, the blue arrow is the refracted light path.

The normal surface is shown as a vertical line. The incident beam hits with an angle <math>\Theta_0\,\!</math>, and the refracted beam has an angle of <math>\Theta_m\,\!</math>. The difference in these two angles is what makes light appear to bend. D has to be the same for the incident beam as the refracted beam. Using geometries of rectangles and triangles the <math>\lambda_0\,\!</math> depends on the sine of <math>\Theta_0\,\!</math>, and <math>\lambda_0\,\!</math> depends on the sine of <math>\Theta_0\,\!</math>.

<math>\overrightarrow{\lambda_0} = \overrightarrow{d} \; sin \; \theta_0\,\!</math>

<math>\overrightarrow{\lambda_m} =\overrightarrow{d} \; sin\;\theta_m\,\!</math>

<math>\frac{\overrightarrow{\lambda_0}} {sin\;\theta_0} = \frac{\overrightarrow{\lambda_m}} {sin\;\theta_m} \equiv \frac{\overrightarrow{\lambda_0}} {n\; sin\;\theta_m}\,\!</math>

<math>n=\frac {sin\;\theta_0} {sin\;\theta_m}\,\!</math>

See also Total Internal Reflection in the context of Optical Fibers

See Wikipedia Refractive index

Index of Refraction and Wavelength

As light passes from a vacuum into a medium with an index of refraction of 2, the wavelength get cut in half, and therefore it will take twice as long for to get through the medium. Again the frequency does not change.

The index of refraction does not have a fixed value for a material, it depends on the wavelength. Index of refraction is a function of the wavelength. If a photon has the right energy to be absorbed it will be interact differently than another photon which is in the transparent range for a material.

<math>v_m = \lambda_m \cdot v = \frac {\lambda_0} {n_m} \cdot v\,\!</math>

When light penetrates a material the frequency n is not affected but the wavelength is. Light will be reflected symmetrically. In a perfectly smooth specular (from the latin speculum- meaning mirror) surface the angle of incidence is equal to the angle of reflection. If you have rough surface light will be reflect in all directions causing diffuse reflection.

The index of refraction is the ratio of <math>sin \theta_0\,\!</math> over <math>sin \theta_m\,\!</math>

<math>\theta_0\ > \theta_m\,\!</math>

So when you have two different materials n₁ and n₂, the ratio of the indices of refraction equals the ratio of the sine of the angles. This is Snell's law.

<math>\frac {n_1} {n_2} = \frac {sin \; \theta_2} {sin \; \theta_2}\,\!</math>

or

<math>n_1 sin \; \theta_1 = n_2 sin \; \theta_2\,\!</math>

Previous Topic

Return to Basics of Light Menu

Next Topic