Difference between revisions of "Dispersion and Attenuation Phenomena"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| (40 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
<td style="text-align: left; width: 33%">[[Optical Fiber Waveguides|Previous Topic]]</td> | <td style="text-align: left; width: 33%">[[Optical Fiber Waveguides|Previous Topic]]</td> | ||
<td style="text-align: center; width: 33%">[[Main_Page#Optical Fibers, Waveguides, and Lasers|Return to Optical Fibers, Waveguides, and Lasers Menu]]</td> | <td style="text-align: center; width: 33%">[[Main_Page#Optical Fibers, Waveguides, and Lasers|Return to Optical Fibers, Waveguides, and Lasers Menu]]</td> | ||
<td style="text-align: right; width: 33%">[[Lasers|Next Topic]]</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
| Line 44: | Line 45: | ||
:<math>\Delta \tau^ {SI} = 6.76 | :<math>\Delta \tau^ {SI} = 6.76 \times 10^{-8}\,\!</math> or 68 ns | ||
This means that for a gigabyte transfer rate after only one km there would be | This means that for a gigabyte transfer rate after only one km there would be 70 bits that have overlapped and would be lost due to intermodal dispersion. | ||
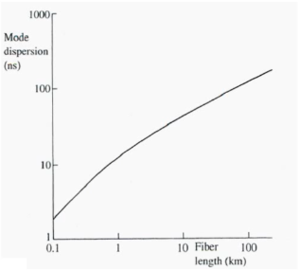
[[Image:Mode_dispersion.png|thumb|300px|]] | [[Image:Mode_dispersion.png|thumb|300px|Over long distances the rate of dispersion reduces because of bends in the cable]] | ||
At distances larger than 1km the intermodal dispersion becomes approximately proportional to the square root of the length and is a significant limiting factor. | At distances larger than 1km the intermodal dispersion becomes approximately proportional to the square root of the length and is a significant limiting factor. | ||
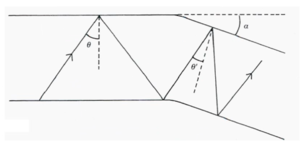
[[Image:Mode_coupling.png|thumb|300px|]] | [[Image:Mode_coupling.png|thumb|300px|Recoupling tends to reduce dispersion]] | ||
The lower rate of increase of dispersion at longer distances is due to mode coupling. Long fibers are not perfectly straight but have small kinks or microbends. A bend acts to realign a mode by slightly changing the angle of incidence over the bended portion. This additive effect tends to recouple or reduce the dispersion of modes that had become dispersed. | The lower rate of increase of dispersion at longer distances is due to mode coupling. Long fibers are not perfectly straight but have small kinks or microbends. A bend acts to realign a mode by slightly changing the angle of incidence over the bended portion. This additive effect tends to recouple or reduce the dispersion of modes that had become dispersed. | ||
Intermodal dispersion may be alleviated by either using a single mode fiber ( a fiber with a V parameter < π/2), or by designing a fiber where the mode velocities are more nearly equal as in a graded index fiber. | Intermodal dispersion may be alleviated by either using a single mode fiber ( a fiber with a V parameter < π/2), or by designing a fiber where the mode velocities are more nearly equal as in a graded index fiber. | ||
<br clear='all'> | |||
===Graded index fibers === | ===Graded index fibers === | ||
It is possible to build materials that have a progessively changing index of refraction over a given thickness. | |||
For graded index fiber in which the indices of refraction of the core and cladding are very close the modal dispersion can be calculated as: | |||
:<math>\frac {\Delta \tau ^{GI}_{min}} {\Delta \tau ^ {SI}} \approx \frac {\Delta } {8} << 1\,\!</math> | |||
With | With | ||
| Line 69: | Line 74: | ||
:<math>\Delta \approx \frac {n_1 – n_2} {n_1}\,\!</math> | :<math>\Delta \approx \frac {n_1 – n_2} {n_1}\,\!</math> | ||
when n<sub>1</sub>~n<sub>2</sub> | |||
Example | Example | ||
| Line 74: | Line 80: | ||
For n1 = 1.48, n2= 1.46 over a distance of 1km | For n1 = 1.48, n2= 1.46 over a distance of 1km | ||
:<math>\Delta = \frac (1.48^2 -1.46^2) 2 | :<math>\Delta = \frac {(1.48^2 -1.46^2)} {2 \times 1.48^2}\,\!</math> = 0.0134 | ||
Then | Then | ||
:<math>\Delta \tau^{GI} | :<math>\Delta \tau^{GI} \approx \frac {1 \times 10^3 \times 1.48} {8 \times 3 \times 10^8} (0.0134) ^2 = 1.1 \times 10^{-10}s\,\!</math> | ||
This is approximately 600 smaller than the mode dispersion calculated for a step index fiber where | |||
:<math>\Delta \tau^{SI}= 6.7 \times 10^{-8}s\,\!</math> | |||
=== Single mode Fibers === | === Single mode Fibers === | ||
| Line 87: | Line 95: | ||
In order to achieve single mode propagation the core radius a must be: | In order to achieve single mode propagation the core radius a must be: | ||
:<math> | :<math>a < \frac {2.405 \lambda_0} {2\pi(n^{2}_{1} - n^{2}_{2})^{1/2}}\,\!</math> | ||
In theory the single mode will propagate no matter how small the value of ''a''. However, as ''a'' decreases the mode extends increasingly into the cladding, losing energy and thus being highly attenuated. Therefore it is better to keep ''a'' very close to maximum value for single mode diameter. | In theory the single mode will propagate no matter how small the value of ''a''. However, as ''a'' decreases the mode extends increasingly into the cladding, losing energy and thus being highly attenuated. Therefore it is better to keep ''a'' very close to maximum value for single mode diameter. | ||
| Line 110: | Line 118: | ||
:<math>\Delta \tau^{mat} \approx \frac {L \lambda^2_0}{c} \frac {d^2 n} {d \lambda^2_0} \frac {\lambda_0}{\lambda_0}\,\!</math> | :<math>\Delta \tau^{mat} \approx \frac {L \lambda^2_0}{c} \frac {d^2 n} {d \lambda^2_0} \frac {\lambda_0}{\lambda_0}\,\!</math> | ||
[[Image:Dispersion_wavelength.png|thumb| | [[Image:Dispersion_wavelength.png|thumb|400px|Variation in the second order derivation of index refraction with respect to wavelength]] | ||
The graph shows the variation in the second order derivation of index refraction with respect to wavelength. | The graph shows the variation in the second order derivation of index refraction with respect to wavelength. | ||
| Line 128: | Line 136: | ||
=== Waveguide dispersion === | === Waveguide dispersion === | ||
[[Image:Profile_dispersion.png|thumb| | [[Image:Profile_dispersion.png|thumb|400px|Waveguide dispersion is minimal at 1.3μm and 1.4μm wavelength for Si0<sub>2</sub>]] | ||
Waveguide dispersion arises because the mode propagation velocity itself depends on wavelength regardless of any refractive index variation of the medium. Waveguide dispersion can not be neglected. | Waveguide dispersion arises because the mode propagation velocity itself depends on wavelength regardless of any refractive index variation of the medium. Waveguide dispersion can not be neglected. | ||
| Line 135: | Line 143: | ||
Attenuation: intrinsic fiber losses. | Attenuation: intrinsic fiber losses. | ||
attenuation = :<math>\frac { 10 log | attenuation = :<math>\frac { 10 log _{10} (P_i / P_f)}{L} dB km ^{-1}\,\!</math> | ||
where | where | ||
| Line 154: | Line 162: | ||
=== Absorption losses === | === Absorption losses === | ||
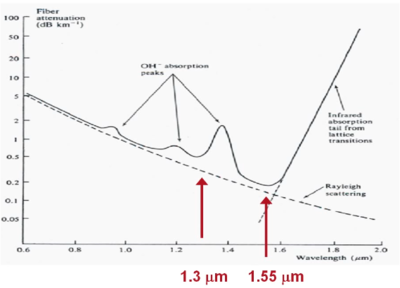
[[Image:Absorption_attenuation.png|thumb| | [[Image:Absorption_attenuation.png|thumb|400px|Patterns for absorption by wavelength for SiO<sub>2</sub>]] | ||
Pure silicon would have virtually no absorption in the critical wavelengths. Absorption losses in the visible and near infrared regions arise mainly from the presence of impurities such as traces of transition metal ions (eg. Fe<sup>3+</sup> Cu<sup>2+</sup> or hydoxyl ions (0H<sup>-</sup>). Dramatic successes in reducing fiber losses come from better control of impurity concentrations of transition metal ions. It is very difficult to eliminate OH<sup>-</sup> bonds (from Si0<sub>2</sub>). These are responsible for overtones of vibration and absorption peaks at .95 μm, 0.24 μm and 1.39 μm. The dashed line is the background Rayleigh scattering. Above 1.6 μm there is a rapid increase in infrared absorption from lattice transitions. So there are two windows for absorption at 1.3 μm and 1.55 μm. Thus the combination of all scattering and attenuation phenomena can be optimized for these two wavelengths, which are the common telecommunications wavelengths. | Pure silicon would have virtually no absorption in the critical wavelengths. Absorption losses in the visible and near infrared regions arise mainly from the presence of impurities such as traces of transition metal ions (eg. Fe<sup>3+</sup> Cu<sup>2+</sup> or hydoxyl ions (0H<sup>-</sup>). Dramatic successes in reducing fiber losses come from better control of impurity concentrations of transition metal ions. It is very difficult to eliminate OH<sup>-</sup> bonds (from Si0<sub>2</sub>). These are responsible for overtones of vibration and absorption peaks at .95 μm, 0.24 μm and 1.39 μm. The dashed line is the background Rayleigh scattering. Above 1.6 μm there is a rapid increase in infrared absorption from lattice transitions. So there are two windows for absorption at 1.3 μm and 1.55 μm. Thus the combination of all scattering and attenuation phenomena can be optimized for these two wavelengths, which are the common telecommunications wavelengths. When working with a few miles, there is no need to regenerate the signal. In this case, it is beneficial to work at 1.3 μm since there is less dispersion loss. Theses are the types of compromises that engineers are looking at. | ||
To date some of the lowest attenuations have obtained with GeO<sub>2</sub> - doped SiO<sub>2</sub> fibers which have attenuations of about .2 dB km<sup>-1</sup> at 1.55 μm. This is close to the limit of Rayleigh scattering. This still is high enough that a cross Atlantic cable needs to be reamplified along the way. | To date some of the lowest attenuations have obtained with GeO<sub>2</sub> - doped SiO<sub>2</sub> fibers which have attenuations of about .2 dB km<sup>-1</sup> at 1.55 μm. This is close to the limit of Rayleigh scattering. This still is high enough that a cross Atlantic cable needs to be reamplified along the way. | ||
== Optical Fiber Materials == | == Optical Fiber Materials == | ||
| Line 167: | Line 174: | ||
The two types of materials that satisfy these criteria are silica (Si0<sub>2</sub>) and various plastics. | The two types of materials that satisfy these criteria are silica (Si0<sub>2</sub>) and various plastics. | ||
=== Silica fiber === | |||
Pure silica has an index of refraction that is on the order of 1.45 at one micron. Wavelengths are usually discussed in vacuum or in air; not what the wavelength becomes in the material itself. Doping is used to build up the difference in index of refraction between the core and the cladding. (the core has to have higher index of refraction than the cladding) For silica, the most common dopants are titania (TiO<sub>2</sub>), alumina, (Al<sub>2</sub>O3) or germania(GeO<sub>2</sub>), which lead to the highest index of refraction. The best fibers that have been obtained so far have Germania-doped silica for the core. Boria (B<sub>2</sub>O<sub>3</sub>) or fluorine tends to decrease the refractive index of the silica matrix so it is best to use them in the claddings. Therefore, germania-doped cores and fluorine-doped claddings are typical fibers that are being used. | |||
The doping process can’t change the index of refraction a lot so the differences in indices between the core and the cladding are not that big. Therefore the fibers have rather small numerical apertures on the order of 0.2. Typical multimode fibers, step-index fibers, usually have diameters that are around 200 μm and a cladding that of an additional 50 μm | |||
But besides those thick fibers, there are also single-mode fibers which must be a just a few microns so that there is just a single-mode that can propagate. When fabricating graded-index fibers by doping the core with, for example, germanium oxide, a larger concentration in the center of the core is obtained and the doping level gradually decreases towards the outside of the core. So you have the profile with a gradually decreasing index of refraction as you move from the center of the core towards its edge. | |||
Both graded-index and single mode silica fibers are readily available. In silica fibers, besides the core and the cladding, there is also a plastic coating but it has no optical activity. It is just there to protect the cladding and the core from any chemical or physical damage. | |||
=== Plastic fiber === | |||
Up until a few years ago, new types of fibers were exclusively that for local-area networks because of the usual losses; but things are changing. These new fibers are based on plastics. While in the case of silica fibers, both the core and the cladding are made essentially of silica, in plastic fibers the core and cladding is made of two different plastics. Therefore, larger numerical apertures (ie 0.4 or greater) can be obtained since larger differences in indices between the core and the cladding can be designed. Polymethyl methacrylate (PMMA, n= 1.495) is a material that is considered quite a bit for the core. Fluoroalkyl methacrylate with an index of refraction of n=1.402 can be used for the cladding. Thus, the indices have a much larger difference than in the case of silica fibers. | |||
In those plastics, the major source of attenuation is due to overtones of C-H vibrations. There is also large Rayleigh scattering from macromolecules. However, over shorter distances, for instance local area networks (LAN) at the level of building ( a few hundred meters), much larger losses from plastic can be worked with. Plastic fiber’s can be tied in a knot without it breaking and still transmit the light guided through the fiber. As long as the optical signal is not sent too far, the fibers are very useful because of their intrinsic flexibility. For example, a car could use plastic fiber to send optical signals from the various sensors to the central computer. Plastic fibers could easily bend along the snaking path within the body. <br clear='all'> | |||
[[Image:Pmma_attenuation.png|thumb|400px|Attenuation for plot for PMMA]] | |||
There is much progress that has been done as well in terms of the quality of the fibers. This graph shows the attenuation that is typical for a PMMA fiber in terms of the core of 150-200 decibels per kilometer. Silica fibers at 1.55 micron has an attenuation of only 0.2 decibel per kilometer. The strong attenuation with PMMA is essentially due to the C-H vibrations. A number of researchers, for instance researchers in Japan have designed fibers made of derivatives of PMMA in which all the hydrogens are replaced by fluorines. Then the C-H vibrations are largely out of the range of the normal transmission wavelengths ( that is 570nm and 650 nm which are associated with red-emitting LEDs). | |||
The progress that has been made in reducing the attenuation in plastic fibers is remarkable. Now people are discussing using plastic fibers for very long distances. The goal is to move away from those C-H bonds and find new elements that can substitute the hydrogens in these plastics so that a completely different attenuation profile can be obtained. | |||
See Wikipedia [http://en.wikipedia.org/wiki/Optical_fiber#Materials Fiber Optic Materials] | See Wikipedia [http://en.wikipedia.org/wiki/Optical_fiber#Materials Fiber Optic Materials] | ||
== Optical communications systems == | |||
An optical communication system means that there is information or a light signal that is sent somewhere by optical fiber. The goal is to modulate the signal or one of the characteristics of the signal so that the information can be obtained at the end of the line. The modulation can be made on various characteristics of the light such as variation in amplitude, irradiance or intensity (which is related to the electric field of the light), frequency, the phase of the light, and the polarization of the light. When relying on light at optical frequencies ( those on the order of visible light) modulation of the intensity (or irradiance) of signal is used. | |||
There are two types of modulation. Either a analog signal or digital signal (analog modulation or digital modulation) can be used. A simple example that uses modulation is sending a voice signal. | |||
=== Analog modulation === | |||
When you pick up the phone, the voice is first transmitted into an electrical signal which is a time varying modulation of the voltage. That signal needs to be sent to the electrical fiber in the form of a modulation of the light signal. This process can be done in an analog fashion. That input information on the electrical voltage continuously varies the parameter of intensity that is modulated for the light. In this case, at any point in time, when the voltage increases, the intensity of your light signal increases; the voltage decreases, the intensity of your light decreases. There is a one to one relationship between the original signal amplitude and the magnitude of the wave parameter (irradiance). | |||
=== Digital modulation === | |||
[[Image:Analogdigital.gif|thumb|550px|In binary digital modulation the information carrier can assume one two discrete states "zero" or "one"]] | |||
For digital modulation, instead of monitoring the value of the voltage continuously in the input voltage, the input signal is sampled at regular intervals. The sampled value is converted into a binary number which then is used to control the amplitude of a light carrier. In other words, either a pulse (acknowledged as a one) or no pulse (a zero) will be sent. | |||
This is a simple example where the binary information is sent with 3 bits. However in real systems, the result of the measurement is sent through 8 bits. At the receiving end the on or off status of the signal is monitored 4 times each time interval for the four binary bits. The resultant binary number measures the amplitude of the original analog signal. | |||
Television signals are now transmitted with digital signals. The advantage is that if the signal is degraded, information is carried accurately up to the point it is not carried at all. This means for most viewers the picture looks perfect. However other viewers may not be able to see an picture at all while they were able to get a scratchy analog signal before the digital conversion in 2009. | |||
Consider a system to carry telephone conversations from here to Japan. The first question that you have to ask is: with my input signal, how frequently do I have to sample that signal in order to have an accurate representation of the input signal? This important question is the reason why there is so much attention paid into the information theory. The sampling theorem states that you have to maintain and keep the integrity of the input information and therefore, we must sample at a rate that is twice as large as the highest frequency of your input signal. For example, the human voice can go up to about 4 kilohertz so you have to sample at a rate of 8 kilo hertz. This means that you have to sample the variation of the noise 8000 times per second (8000 bps). The next step is to measure the voltage corresponding to that signal. Using an 8 bit number to represent the measurement results in a bit rate that is 16 times the highest frequency. A digital scheme requires a much higher system frequency bandwidth than would be needed for a corresponding analog signal. | |||
So 8000 times per second the result of each measurement is sent in the form of a string of 8 pulses or no pulses. This means that about 64 kilo bit of information has to be transmitted per second(8 bits x 8000 bps= 64 kbps). This is the telecommunication bandwidth. Note: the term bandwidth in this context is completely different from the bandwidth or bandgap between the conduction band and valence band of a chemical. | |||
The bandwidth for optical fibers is typically on the order of 1 gigabit per second. Continuing the example from the previous slide, a phone conversation requires 64 kilobits per second. That means that you can actually have multiple signals superimposed one over the other in parallel. This means 15,000 telephone conversations that can go to the other side of the ocean. Also, if you were to fax a document with the resolution that is usually used, you can send 60,000 pages per second. The only engineering involved includes sending those 15,000 phone conversations along the same fiber without scrambling them up on the way to their destination. | |||
In general when one looks at all the applications of non-linear optics (or what is referred to as electro optic modulation), modulation speed is one of the most important aspects. Using pi electrons moving along a back bone, one can have a very fast response allowing modulation of the signal to occur at a rate beyond a gigabit per second. | |||
Although there are discussions regarding this application, there is a significant investment in optical fibers that are already laid down at the bottom of the ocean. New fibers would have to be laid to take advantage of this new higher speed technology. | |||
[[category:Photonics applications]] | |||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
<td style="text-align: left; width: 33%">[[Optical Fiber Waveguides|Previous Topic]]</td> | <td style="text-align: left; width: 33%">[[Optical Fiber Waveguides|Previous Topic]]</td> | ||
<td style="text-align: center; width: 33%">[[Main_Page#Optical Fibers, Waveguides, and Lasers|Return to Optical Fibers, Waveguides, and Lasers Menu]]</td> | <td style="text-align: center; width: 33%">[[Main_Page#Optical Fibers, Waveguides, and Lasers|Return to Optical Fibers, Waveguides, and Lasers Menu]]</td> | ||
<td style="text-align: right; width: 33%">[[Lasers|Next Topic]]</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
Latest revision as of 09:13, 23 June 2010
| Previous Topic | Return to Optical Fibers, Waveguides, and Lasers Menu | Next Topic |
Dispersion and attenuation phenomena
As waves propagate they may become wider; this is known as dispersion. The amplitude of waves may decrease; this is known as attenuation. Low attenuation is critical for long distance communication fibers since reamplification of the signal is expensive and complicated. Dispersion causes an overlap of information carrying pulses which decreases the information carrying capacity of an amplitude modulated fiber. We want to design fibers that can carry a very sharp pulse with little dispersion.
Intermodal dispersion
The speed that a ray travels down a fiber depends on its internal angle q. When there are several modes at different angles then the path that each mode takes is different and the arrival time of a bit is different. The time it takes for a mode to move down a fiber:
Minimum for q ~ 90 °
Maxium for q = qc
- <math>\Delta \tau_{min} = \frac {Ln_1}{ c sin 90 ^{\circ}} = \frac {Ln_1} {c}\,\!</math>
- <math>\Delta \tau_{max} = \frac {Ln_1}{ c sin \theta_ c} = \frac {Ln^2_1} {cn_2}\,\!</math>
This makes sense because if the angle is 90° the mode can propagate down the center without interacting with the cladding.
The maximum difference in time of travel of two modes (one mode at 90° and one at cut-off) can be written:
- <math>\Delta \tau^{SI} = \Delta \tau_{max} – \Delta \tau_{min}\,\!</math>
- <math>\Delta \tau^{SI} = \frac {L} {c} \frac {n_1} {n_2} (n_1 – n_2)\,\!</math>
Thus the Dt (and therefore intermodal dispersion ) is proportional to the difference between the indices of refraction. For small fiber lengths up to 1 km the intermodal dispersion is proportional to L.
Example:
For n1 = 1.48 , n2 = 1.46 and L = 1km
- <math>\Delta \tau^ {SI} = \frac {1 \times 10^3 } {1 \times 10^8} \frac {1.48} {1.46} (1.48 - 1.46)s\,\!</math>
So
- <math>\Delta \tau^ {SI} = 6.76 \times 10^{-8}\,\!</math> or 68 ns
This means that for a gigabyte transfer rate after only one km there would be 70 bits that have overlapped and would be lost due to intermodal dispersion.
At distances larger than 1km the intermodal dispersion becomes approximately proportional to the square root of the length and is a significant limiting factor.
The lower rate of increase of dispersion at longer distances is due to mode coupling. Long fibers are not perfectly straight but have small kinks or microbends. A bend acts to realign a mode by slightly changing the angle of incidence over the bended portion. This additive effect tends to recouple or reduce the dispersion of modes that had become dispersed.
Intermodal dispersion may be alleviated by either using a single mode fiber ( a fiber with a V parameter < π/2), or by designing a fiber where the mode velocities are more nearly equal as in a graded index fiber.
Graded index fibers
It is possible to build materials that have a progessively changing index of refraction over a given thickness.
For graded index fiber in which the indices of refraction of the core and cladding are very close the modal dispersion can be calculated as:
- <math>\frac {\Delta \tau ^{GI}_{min}} {\Delta \tau ^ {SI}} \approx \frac {\Delta } {8} << 1\,\!</math>
With
- <math>\Delta \approx \frac {n_1 – n_2} {n_1}\,\!</math>
when n1~n2
Example
For n1 = 1.48, n2= 1.46 over a distance of 1km
- <math>\Delta = \frac {(1.48^2 -1.46^2)} {2 \times 1.48^2}\,\!</math> = 0.0134
Then
- <math>\Delta \tau^{GI} \approx \frac {1 \times 10^3 \times 1.48} {8 \times 3 \times 10^8} (0.0134) ^2 = 1.1 \times 10^{-10}s\,\!</math>
This is approximately 600 smaller than the mode dispersion calculated for a step index fiber where
- <math>\Delta \tau^{SI}= 6.7 \times 10^{-8}s\,\!</math>
Single mode Fibers
In order to achieve single mode propagation the core radius a must be:
- <math>a < \frac {2.405 \lambda_0} {2\pi(n^{2}_{1} - n^{2}_{2})^{1/2}}\,\!</math>
In theory the single mode will propagate no matter how small the value of a. However, as a decreases the mode extends increasingly into the cladding, losing energy and thus being highly attenuated. Therefore it is better to keep a very close to maximum value for single mode diameter.
This can be done by making the core and cladding refractive indexes very close together. In practice single mode fibers are made with a numerical aperature (NA) of 0.1. When used with radiation that is typically used in telecommunications 1.3 μ m and 1.6 μ m, single mode fibers have core diameters between 5 μ m and 10 μ m.
Dispersion in single-mode fibers
By using single mode fibers, the problems associated with intermodal dispersion are completely avoided. However there are three other sources of dispersion; material (chromatic) dispersion, profile dispersion and waveguide dispersion.
Material dispersion arises because of the wavelength dependence of the refractive index of the fiber material. Light is never perfectly monochromatic. Any pulse of light consists of a finite spread of wavelengths that travel with a group velocity Vg given by:
- <math>V_g = \frac {d \omega} {dk}\,\!</math>
where
- <math>\omega = 2 \pi n\,\!</math>
- <math>k=\frac { 2\pi}{\lambda}\,\!</math> and lambda is the wavelength in the material
A radiation with finite wavelength spread Δ λ 0 will have a dispersion over the length (Δ τ mat) given by
- <math>\Delta \tau^{mat} \approx \frac {L \lambda^2_0}{c} \frac {d^2 n} {d \lambda^2_0} \frac {\lambda_0}{\lambda_0}\,\!</math>
The graph shows the variation in the second order derivation of index refraction with respect to wavelength.
For silica the temporal dispersion can be eliminated by using a wavelength of 1.3 μm. It is still pretty good in the range 1.3 to 1.6 which is also critical with respect to attenuation processes.
A semiconductor laser working at 1550 nm has a linewidth of 3 nm will have a Δ τ mat over 1km of 6.6 x 10-11 whereas GaAs LED operating at 850 nm and a 50 nm linewidth will have a Δ τ mat of 4.2 x 10-9. This clearly shows the superiority of lasers operating at 1550nm.
Profile Dispersion
Profile dispersion arises because of the variation of the quantity Δ with wavelength
- <math>\Delta \approx \frac {n_1- n_2} {n_1}\,\!</math>
The index of refraction of different materials will respond differently to changing wavelength. In practice most fibers use silica (with slightly different dopants) for both the core and cladding so the dependence of Δ on wavelength is very small and can be ignored. This is an advantage of having n1 and n2 very close to one another.
Waveguide dispersion
Waveguide dispersion arises because the mode propagation velocity itself depends on wavelength regardless of any refractive index variation of the medium. Waveguide dispersion can not be neglected.
The graph shows both material and waveguide dispersion as a function of wavelength. Temporal dispersion is measured in units of picosecond μm -1 km -1. Dispersion remains small in the 1.3 to 1.5 μm wavelength range.
Attenuation: intrinsic fiber losses.
attenuation = :<math>\frac { 10 log _{10} (P_i / P_f)}{L} dB km ^{-1}\,\!</math>
where
- <math>p_i\,\!</math> is the input power
- <math>p_f\,\!</math> is the final power
- <math>L\,\!</math> is length
Attenuation is expressed in decibels. This would have the unit Bells per meter, and multiplied by 10 it becomes decibels.
Intrinsic losses in silica fibers have two main sources; scattering losses and absorption losses.
Scattering losses
Fibers of silica are an amorphous materials. Crystalline materials would have diffraction losses that would quickly attenuate the beam. Scattering losses is caused by fluctuation in the refractive index through the material with each irregularity acting as point scattering center. The scale of fluctuations is in the order of λ/10. This Rayleigh scattering absorption coefficient varies as λ -4. There is a factor of 16 difference in scattering between blue light and red light. The larger the wavelength the smaller the scattering.
Absorption losses
Pure silicon would have virtually no absorption in the critical wavelengths. Absorption losses in the visible and near infrared regions arise mainly from the presence of impurities such as traces of transition metal ions (eg. Fe3+ Cu2+ or hydoxyl ions (0H-). Dramatic successes in reducing fiber losses come from better control of impurity concentrations of transition metal ions. It is very difficult to eliminate OH- bonds (from Si02). These are responsible for overtones of vibration and absorption peaks at .95 μm, 0.24 μm and 1.39 μm. The dashed line is the background Rayleigh scattering. Above 1.6 μm there is a rapid increase in infrared absorption from lattice transitions. So there are two windows for absorption at 1.3 μm and 1.55 μm. Thus the combination of all scattering and attenuation phenomena can be optimized for these two wavelengths, which are the common telecommunications wavelengths. When working with a few miles, there is no need to regenerate the signal. In this case, it is beneficial to work at 1.3 μm since there is less dispersion loss. Theses are the types of compromises that engineers are looking at.
To date some of the lowest attenuations have obtained with GeO2 - doped SiO2 fibers which have attenuations of about .2 dB km-1 at 1.55 μm. This is close to the limit of Rayleigh scattering. This still is high enough that a cross Atlantic cable needs to be reamplified along the way.
Optical Fiber Materials
Optic fiber materials must satisfy certain conditions to be of practical use.
- They must be highly transparent to the radiation being used (the telecommunication frequencies or specific wavelength for example light guides to supply pumped lasers)
- It must be possible and efficient to fabricate the core and cladding structures.
- It must be reasonable flexible
The two types of materials that satisfy these criteria are silica (Si02) and various plastics.
Silica fiber
Pure silica has an index of refraction that is on the order of 1.45 at one micron. Wavelengths are usually discussed in vacuum or in air; not what the wavelength becomes in the material itself. Doping is used to build up the difference in index of refraction between the core and the cladding. (the core has to have higher index of refraction than the cladding) For silica, the most common dopants are titania (TiO2), alumina, (Al2O3) or germania(GeO2), which lead to the highest index of refraction. The best fibers that have been obtained so far have Germania-doped silica for the core. Boria (B2O3) or fluorine tends to decrease the refractive index of the silica matrix so it is best to use them in the claddings. Therefore, germania-doped cores and fluorine-doped claddings are typical fibers that are being used.
The doping process can’t change the index of refraction a lot so the differences in indices between the core and the cladding are not that big. Therefore the fibers have rather small numerical apertures on the order of 0.2. Typical multimode fibers, step-index fibers, usually have diameters that are around 200 μm and a cladding that of an additional 50 μm
But besides those thick fibers, there are also single-mode fibers which must be a just a few microns so that there is just a single-mode that can propagate. When fabricating graded-index fibers by doping the core with, for example, germanium oxide, a larger concentration in the center of the core is obtained and the doping level gradually decreases towards the outside of the core. So you have the profile with a gradually decreasing index of refraction as you move from the center of the core towards its edge.
Both graded-index and single mode silica fibers are readily available. In silica fibers, besides the core and the cladding, there is also a plastic coating but it has no optical activity. It is just there to protect the cladding and the core from any chemical or physical damage.
Plastic fiber
Up until a few years ago, new types of fibers were exclusively that for local-area networks because of the usual losses; but things are changing. These new fibers are based on plastics. While in the case of silica fibers, both the core and the cladding are made essentially of silica, in plastic fibers the core and cladding is made of two different plastics. Therefore, larger numerical apertures (ie 0.4 or greater) can be obtained since larger differences in indices between the core and the cladding can be designed. Polymethyl methacrylate (PMMA, n= 1.495) is a material that is considered quite a bit for the core. Fluoroalkyl methacrylate with an index of refraction of n=1.402 can be used for the cladding. Thus, the indices have a much larger difference than in the case of silica fibers.
In those plastics, the major source of attenuation is due to overtones of C-H vibrations. There is also large Rayleigh scattering from macromolecules. However, over shorter distances, for instance local area networks (LAN) at the level of building ( a few hundred meters), much larger losses from plastic can be worked with. Plastic fiber’s can be tied in a knot without it breaking and still transmit the light guided through the fiber. As long as the optical signal is not sent too far, the fibers are very useful because of their intrinsic flexibility. For example, a car could use plastic fiber to send optical signals from the various sensors to the central computer. Plastic fibers could easily bend along the snaking path within the body.
There is much progress that has been done as well in terms of the quality of the fibers. This graph shows the attenuation that is typical for a PMMA fiber in terms of the core of 150-200 decibels per kilometer. Silica fibers at 1.55 micron has an attenuation of only 0.2 decibel per kilometer. The strong attenuation with PMMA is essentially due to the C-H vibrations. A number of researchers, for instance researchers in Japan have designed fibers made of derivatives of PMMA in which all the hydrogens are replaced by fluorines. Then the C-H vibrations are largely out of the range of the normal transmission wavelengths ( that is 570nm and 650 nm which are associated with red-emitting LEDs). The progress that has been made in reducing the attenuation in plastic fibers is remarkable. Now people are discussing using plastic fibers for very long distances. The goal is to move away from those C-H bonds and find new elements that can substitute the hydrogens in these plastics so that a completely different attenuation profile can be obtained.
See Wikipedia Fiber Optic Materials
Optical communications systems
An optical communication system means that there is information or a light signal that is sent somewhere by optical fiber. The goal is to modulate the signal or one of the characteristics of the signal so that the information can be obtained at the end of the line. The modulation can be made on various characteristics of the light such as variation in amplitude, irradiance or intensity (which is related to the electric field of the light), frequency, the phase of the light, and the polarization of the light. When relying on light at optical frequencies ( those on the order of visible light) modulation of the intensity (or irradiance) of signal is used.
There are two types of modulation. Either a analog signal or digital signal (analog modulation or digital modulation) can be used. A simple example that uses modulation is sending a voice signal.
Analog modulation
When you pick up the phone, the voice is first transmitted into an electrical signal which is a time varying modulation of the voltage. That signal needs to be sent to the electrical fiber in the form of a modulation of the light signal. This process can be done in an analog fashion. That input information on the electrical voltage continuously varies the parameter of intensity that is modulated for the light. In this case, at any point in time, when the voltage increases, the intensity of your light signal increases; the voltage decreases, the intensity of your light decreases. There is a one to one relationship between the original signal amplitude and the magnitude of the wave parameter (irradiance).
Digital modulation
For digital modulation, instead of monitoring the value of the voltage continuously in the input voltage, the input signal is sampled at regular intervals. The sampled value is converted into a binary number which then is used to control the amplitude of a light carrier. In other words, either a pulse (acknowledged as a one) or no pulse (a zero) will be sent.
This is a simple example where the binary information is sent with 3 bits. However in real systems, the result of the measurement is sent through 8 bits. At the receiving end the on or off status of the signal is monitored 4 times each time interval for the four binary bits. The resultant binary number measures the amplitude of the original analog signal.
Television signals are now transmitted with digital signals. The advantage is that if the signal is degraded, information is carried accurately up to the point it is not carried at all. This means for most viewers the picture looks perfect. However other viewers may not be able to see an picture at all while they were able to get a scratchy analog signal before the digital conversion in 2009.
Consider a system to carry telephone conversations from here to Japan. The first question that you have to ask is: with my input signal, how frequently do I have to sample that signal in order to have an accurate representation of the input signal? This important question is the reason why there is so much attention paid into the information theory. The sampling theorem states that you have to maintain and keep the integrity of the input information and therefore, we must sample at a rate that is twice as large as the highest frequency of your input signal. For example, the human voice can go up to about 4 kilohertz so you have to sample at a rate of 8 kilo hertz. This means that you have to sample the variation of the noise 8000 times per second (8000 bps). The next step is to measure the voltage corresponding to that signal. Using an 8 bit number to represent the measurement results in a bit rate that is 16 times the highest frequency. A digital scheme requires a much higher system frequency bandwidth than would be needed for a corresponding analog signal.
So 8000 times per second the result of each measurement is sent in the form of a string of 8 pulses or no pulses. This means that about 64 kilo bit of information has to be transmitted per second(8 bits x 8000 bps= 64 kbps). This is the telecommunication bandwidth. Note: the term bandwidth in this context is completely different from the bandwidth or bandgap between the conduction band and valence band of a chemical.
The bandwidth for optical fibers is typically on the order of 1 gigabit per second. Continuing the example from the previous slide, a phone conversation requires 64 kilobits per second. That means that you can actually have multiple signals superimposed one over the other in parallel. This means 15,000 telephone conversations that can go to the other side of the ocean. Also, if you were to fax a document with the resolution that is usually used, you can send 60,000 pages per second. The only engineering involved includes sending those 15,000 phone conversations along the same fiber without scrambling them up on the way to their destination.
In general when one looks at all the applications of non-linear optics (or what is referred to as electro optic modulation), modulation speed is one of the most important aspects. Using pi electrons moving along a back bone, one can have a very fast response allowing modulation of the signal to occur at a rate beyond a gigabit per second.
Although there are discussions regarding this application, there is a significant investment in optical fibers that are already laid down at the bottom of the ocean. New fibers would have to be laid to take advantage of this new higher speed technology.
| Previous Topic | Return to Optical Fibers, Waveguides, and Lasers Menu | Next Topic |