Difference between revisions of "Electronic Coupling Between Orbitals"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) m |
||
| (28 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[Main_Page#Molecular Orbitals|Return to Molecular Orbitals Menu]] | <table id="toc" style="width: 100%"> | ||
[[Donors and Acceptors|Next Topic]] | <tr> | ||
<td style="text-align: left; width: 33%">[[Polarization and Polarizability|Previous Topic]]</td> | |||
<td style="text-align: center; width: 33%">[[Main_Page#Molecular Orbitals|Return to Molecular Orbitals Menu]]</td> | |||
<td style="text-align: right; width: 33%">[[Donors and Acceptors|Next Topic]]</td> | |||
</tr> | |||
</table> | |||
π-conjugated organic molecules have delocalized electrons which gives rise to useful nonlinear optical qualities. They are the basis of most chromophores. A detailed understanding of the their electronic structure makes it possible to fine-tune their absorption, emission and other electrical properties. | |||
=== Hückel Molecular Orbital Theory=== | |||
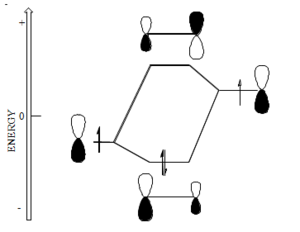
[[Image:Beta-adjacent.png|thumb|200px|Adjacent p orbitals can interact]] | [[Image:Beta-adjacent.png|thumb|200px|Adjacent p orbitals can interact]] | ||
Here we start at the simplest level that is basically derived from a Hückel Molecular Orbital approach in order to understand conjugated systems. π-conjugated molecules have a sigma electron framework and π electron framework. | |||
Here we start at the simplest level that is basically derived from a Hückel Molecular Orbital approach in order to understand conjugated systems. | |||
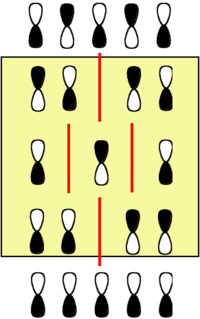
In this model, orbitals that are on atoms that are directly σ-bonded to one another and whose p-orbitals are in a plane can interact. This interaction is called the "electronic coupling" between the orbitals and has units of energy. | In this model, orbitals that are on atoms that are directly σ-bonded to one another and whose p-orbitals are in a plane can interact. This interaction is called the "electronic coupling" between the orbitals and has units of energy. | ||
In the Hückel approximation this energy is the same for all carbon p-orbitals that are adjacent to on another and is called & | In the Hückel approximation this energy is the same for all carbon p-orbitals that are adjacent to on another and is called β. | ||
<br clear='all'> | <br clear='all'> | ||
[[Image:Beta-nonadjacent.png|thumb|200px|Non- Adjacent p orbitals do not interact]] | [[Image:Beta-nonadjacent.png|thumb|200px|Non- Adjacent p orbitals do not interact]] | ||
For atoms that are not adjacent to one another & | For atoms that are not adjacent to one another β is taken to be zero. Thus in the Hückel approximation there is no interaction between nonadjacent atoms. Even if you distort the system so that nonadjacent atoms are very close they will not be considered because there is not bonding. | ||
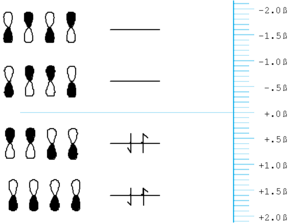
Through this coupling of atomic orbitals, molecular orbitals can formed by a constructive and destructive combination of the atomic orbitals. If you begin to fill the orbitals from the lowest to the highest energy you fill the bonding orbital first. This is also known as the highes occupied molecular orbital (HOMO). The antibonding orbital is known as the lowest unoccupied molecular orbital (LUMO). | Through this coupling of atomic orbitals, molecular orbitals can formed by a constructive and destructive combination of the atomic orbitals. If you begin to fill the orbitals from the lowest to the highest energy you fill the bonding orbital first. This is also known as the highes occupied molecular orbital (HOMO). The antibonding orbital is known as the lowest unoccupied molecular orbital (LUMO). | ||
*The energy of a carbon orbital is taken to be zero, neither stabilized or destabilized. Fluorine would be defined as less than zero. As go to a more electronegative atom you will pull down the energy of the orbital. | *The energy of a carbon orbital is taken to be zero, neither stabilized or destabilized. Fluorine would be defined as less than zero. As go to a more electronegative atom you will pull down the energy of the orbital. | ||
*In ethylene the bonding orbital has no nodes and the antibonding orbital has a node that is in between the atoms. | *In ethylene the bonding orbital has no nodes and the antibonding orbital has a node that is in between the atoms. | ||
*The bonding orbital is basically stabilized by amount roughly equal to & | *The bonding orbital is basically stabilized by amount roughly equal to β and the antibonding orbital is destabilized by a roughly equal amount. In reality, the coupling of the orbitals will be a function orbital overlap which itself depends of how diffuse the orbitals are, their relative orientation and their center to center distance. If bonds are longer the degree of overlap there will be less coupling which decreases the homo / lumo gap. | ||
*An atom more electronegative than carbon will have an p-orbital that lies lower in energy than that of carbon and one more electropositive will have an energy that lies above that of carbon. This will have consequence in the molecular orbitals that are derived from atomic orbitals. | *An atom more electronegative than carbon will have an p-orbital that lies lower in energy than that of carbon and one more electropositive will have an energy that lies above that of carbon. This will have consequence in the molecular orbitals that are derived from atomic orbitals. | ||
=== | === Perturbation theory === | ||
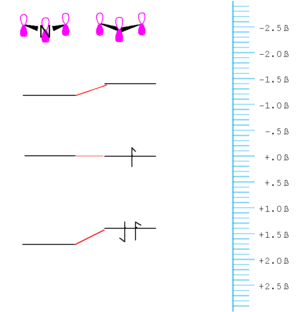
[[Image:Beta- | [[Image:Beta-energydiagram.png|thumb|300px|Bonding between atoms with equal electronegativity]] | ||
If the orbitals that mix are the some energy the mixing can be treated using '''first order perturbation theory'''. | If the orbitals that mix are the some energy the mixing can be treated using '''first order perturbation theory'''. | ||
[[Image:Beta-energydiagram_unequal.png|thumb|300px|Bonding between atoms with unequal electronegativity, for example oxygen and carbon]] | |||
If the orbitals are at different energy they are treated using '''second-order perturbation theory''' in which the energy gap between the orbital is taken into account and in general the mixing of orbitals that are degenerate is greater than those that are not; also the greater the energy difference between the orbital, in general the less the mixing. The amount the bonding orbital is stabilized and the anti-bonding orbital is destabilized decreases. | If the orbitals are at different energy they are treated using '''second-order perturbation theory''' in which the energy gap between the orbital is taken into account and in general the mixing of orbitals that are degenerate is greater than those that are not; also the greater the energy difference between the orbital, in general the less the mixing. The amount the bonding orbital is stabilized and the anti-bonding orbital is destabilized decreases. | ||
| Line 31: | Line 44: | ||
If you promote an electron from the HOMO to the LUMO the dipole moment of the molecule would decrease. | If you promote an electron from the HOMO to the LUMO the dipole moment of the molecule would decrease. | ||
<br clear='all'> | |||
=== Butadiene Orbitals === | === Butadiene Orbitals === | ||
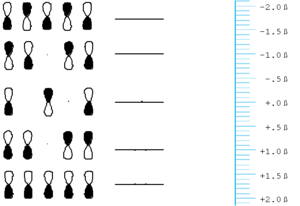
[[Image:Butadiene.png|thumb|300px|]] | [[Image:Butadiene.png|thumb|300px|Orbital energy for diagram for butadiene]] | ||
[[Image:Butadiene-pi-MOs-Spartan-3D-balls.png|thumb|300px|Butadiene with π orbitals (from wikimedia)]] | |||
Butadiene starts with four p orbitals. | Butadiene starts with four p orbitals. | ||
*The energy scale is in terms of & | *The energy scale is in terms of β and the most stable orbital here has the most positive value of β, because β itself is take to have a negative value. | ||
*For each orbital that has nodes, | *For each orbital that has nodes, these will be situated between (not on) atoms. | ||
*The gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) is less than that in ethylene. | *The gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) is less than that in ethylene. | ||
| Line 46: | Line 61: | ||
We can make molecules easier to oxidize and easier reduce as we increase the length and add more orbitals. From an electron chemical standpoint butadiene is a better electron donor. | We can make molecules easier to oxidize and easier reduce as we increase the length and add more orbitals. From an electron chemical standpoint butadiene is a better electron donor. | ||
<br clear='all'> | |||
===Allyl- Odd number of orbitals === | ===Allyl- Odd number of orbitals === | ||
[[Image:Allyl_energy.png|thumb|300px|]] | [[Image:Allyl_energy.png|thumb|300px|Orbital energy diagram for allyl]] | ||
Lets now consider a system with an odd number of atoms, the simplest being allyl. | Lets now consider a system with an odd number of atoms, the simplest being allyl. | ||
| Line 61: | Line 76: | ||
*Allyl can exist as a allyl radical, allyl cation, allyl anion and each with different orbital filling. | *Allyl can exist as a allyl radical, allyl cation, allyl anion and each with different orbital filling. | ||
The energy difference between the lowest and highest orbital of allyl and is less than the difference with ethylene ( 1.4& | The energy difference between the lowest and highest orbital of allyl and is less than the difference with ethylene ( 1.4β compared to 2β). Allyl has a small gap than ethylene. | ||
What do we expect the result of changing the carbon for a more electronegative element to be? | What do we expect the result of changing the carbon for a more electronegative element to be? | ||
| Line 68: | Line 83: | ||
<br clear='all'> | <br clear='all'> | ||
[[Image:Allyl nitrogen.png|thumb|300px|Relative energy levels of carbon chain with and without nitrogen.]] | [[Image:Allyl nitrogen.png|thumb|300px|Relative energy levels of carbon chain with and without nitrogen.]] | ||
For example if you made a molecule allyl cation that has only two electrons in the homo, and then made a corresponding molecule with a nitrogen in the middle. The homo /lumo gap will increase because the HOMO energy level is lowered while the LUMO stays the same. Thus, the most orbitals are stabilized by inclusion of the nitrogen | For example if you made a molecule allyl cation that has only two electrons in the homo, and then made a corresponding molecule with a nitrogen in the middle. The homo /lumo gap will increase because the HOMO energy level is lowered while the LUMO stays the same. Thus, the most orbitals are stabilized by inclusion of the nitrogen. | ||
Note that the orbital that has a node on the central atom is not affected by this change. | Note that the orbital that has a node on the central atom is not affected by this change. | ||
| Line 75: | Line 91: | ||
=== Pentadienyl Radical === | === Pentadienyl Radical === | ||
[[Image:Pentadienyl_energy.png|thumb|300px|]] | [[Image:Pentadienyl_energy.png|thumb|300px|Pentadiene]] | ||
If you consider the pentadienyl anion, radical and cation, that each has nodes on either odd or even atoms in the HOMO or LUMO and that the nodes do not match up in position. The middle orbital has the same energy as carbon. The gap between levels decreases more rapidly than for even numbered orbital molecules. | |||
This is the basis for making some simple predictions about the spectroscopy of so-called cyanine-like molecules upon substitution of atoms along the chain with either electronegative or electropositive elements. Likewise the addition of electron donating and withdrawing groups can have similar effects. | |||
This is the basis for making some simple predictions about the spectroscopy of so-called cyanine-like molecules upon substitution of atoms along the chain with either electronegative or electropositive elements | [[Image:polyene.png|thumb|200px|Polyenes]] | ||
[[Image:polyene.png|thumb| | |||
Another distinction between cyanine-like dyes and polyene like dyes is the in polyene there is a complete reversal of the bond order between the π-bonding HOMO and the π-antibonding LUMO. | Another distinction between cyanine-like dyes and polyene like dyes is the in polyene there is a complete reversal of the bond order between the π-bonding HOMO and the π-antibonding LUMO. | ||
<br clear='all'> | |||
[[Image:Cyanene.png|thumb|200px|Cyanines]]In contrast, in cyanines because typically either the HOMO or the LUMO is non-bonding, and because there are nodes at the atoms rather than between bonds in the frontier orbitals, there tend to be smaller changes in bond-length between the HOMO and LUMO. This will have spectroscopic implications. Anything that pushes electron density onto an atom increases the energy of the atomic orbital associated with that atom. Anything that takes electron density away will decrease the corresponding orbital energy. | |||
[[category:molecular orbitals]] | |||
<br clear='all'> | |||
<table id="toc" style="width: 100%"> | |||
<tr> | |||
<td style="text-align: left; width: 33%">[[Polarization and Polarizability|Previous Topic]]</td> | |||
<td style="text-align: center; width: 33%">[[Main_Page#Molecular Orbitals|Return to Molecular Orbitals Menu]]</td> | |||
<td style="text-align: right; width: 33%">[[Donors and Acceptors|Next Topic]]</td> | |||
</tr> | |||
</table> | |||
Latest revision as of 11:28, 29 December 2009
| Previous Topic | Return to Molecular Orbitals Menu | Next Topic |
π-conjugated organic molecules have delocalized electrons which gives rise to useful nonlinear optical qualities. They are the basis of most chromophores. A detailed understanding of the their electronic structure makes it possible to fine-tune their absorption, emission and other electrical properties.
Hückel Molecular Orbital Theory
Here we start at the simplest level that is basically derived from a Hückel Molecular Orbital approach in order to understand conjugated systems. π-conjugated molecules have a sigma electron framework and π electron framework.
In this model, orbitals that are on atoms that are directly σ-bonded to one another and whose p-orbitals are in a plane can interact. This interaction is called the "electronic coupling" between the orbitals and has units of energy.
In the Hückel approximation this energy is the same for all carbon p-orbitals that are adjacent to on another and is called β.
For atoms that are not adjacent to one another β is taken to be zero. Thus in the Hückel approximation there is no interaction between nonadjacent atoms. Even if you distort the system so that nonadjacent atoms are very close they will not be considered because there is not bonding.
Through this coupling of atomic orbitals, molecular orbitals can formed by a constructive and destructive combination of the atomic orbitals. If you begin to fill the orbitals from the lowest to the highest energy you fill the bonding orbital first. This is also known as the highes occupied molecular orbital (HOMO). The antibonding orbital is known as the lowest unoccupied molecular orbital (LUMO).
- The energy of a carbon orbital is taken to be zero, neither stabilized or destabilized. Fluorine would be defined as less than zero. As go to a more electronegative atom you will pull down the energy of the orbital.
- In ethylene the bonding orbital has no nodes and the antibonding orbital has a node that is in between the atoms.
- The bonding orbital is basically stabilized by amount roughly equal to β and the antibonding orbital is destabilized by a roughly equal amount. In reality, the coupling of the orbitals will be a function orbital overlap which itself depends of how diffuse the orbitals are, their relative orientation and their center to center distance. If bonds are longer the degree of overlap there will be less coupling which decreases the homo / lumo gap.
- An atom more electronegative than carbon will have an p-orbital that lies lower in energy than that of carbon and one more electropositive will have an energy that lies above that of carbon. This will have consequence in the molecular orbitals that are derived from atomic orbitals.
Perturbation theory
If the orbitals that mix are the some energy the mixing can be treated using first order perturbation theory.
If the orbitals are at different energy they are treated using second-order perturbation theory in which the energy gap between the orbital is taken into account and in general the mixing of orbitals that are degenerate is greater than those that are not; also the greater the energy difference between the orbital, in general the less the mixing. The amount the bonding orbital is stabilized and the anti-bonding orbital is destabilized decreases.
As a consequence of this the coefficient of the stabilized orbital is larger on the atom to which it is closer in energy and the same if true for the unfilled orbital. In this example there would be a higher electron density around the oxygen than around the carbon. This molecule would have a dipole moment. The antibonding orbital has a higher coefficient on the carbon. This a proton would tend to react with the oxygen because the highest occupied orbital has a higher electron density with the the oxygen. On the other hand the carbon will be the more electrophillic site. This allows us to make very simple predictions about reactivity.
If you promote an electron from the HOMO to the LUMO the dipole moment of the molecule would decrease.
Butadiene Orbitals
Butadiene starts with four p orbitals.
- The energy scale is in terms of β and the most stable orbital here has the most positive value of β, because β itself is take to have a negative value.
- For each orbital that has nodes, these will be situated between (not on) atoms.
- The gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) is less than that in ethylene.
- The orbital energy are symmetrically disposed around zero.
- The LUMO in butadiene is lower than that in ethylene and the HOMO is higher than that in ethylene. Butadiene should be both easier to reduce than ethylene and easier to oxidize.
We can make molecules easier to oxidize and easier reduce as we increase the length and add more orbitals. From an electron chemical standpoint butadiene is a better electron donor.
Allyl- Odd number of orbitals
Lets now consider a system with an odd number of atoms, the simplest being allyl.
Note that the are several significant similarities and differences between the orbital in allyl and those of butadiene or ethylene:
- The HOMO of allyl radical (anion) is at the some level of a carbon p-orbital (i.e.) it is neither stabilized nor destabilized relative to carbon.
- The HOMO has one node and that node lies on a carbon atom, not between atoms.
- Due to the node between carbon the central carbon (carbon 2) and the fact that in the Hückel approximation there is no interaction between carbons 1 and 3. This orbital neither bonding or antibonding and is thus called non-bonding.
- Allyl can exist as a allyl radical, allyl cation, allyl anion and each with different orbital filling.
The energy difference between the lowest and highest orbital of allyl and is less than the difference with ethylene ( 1.4β compared to 2β). Allyl has a small gap than ethylene.
What do we expect the result of changing the carbon for a more electronegative element to be?
A more electronegative element has its electrons held more tightly and closer to the nucleus and as a result as we noted earlier the energy level of a p-orbital on a more electronegative element should be lower than that of carbon. Therefore it should stabilize molecular orbitals that have significant coefficients on the atom that is more electronegative.
For example if you made a molecule allyl cation that has only two electrons in the homo, and then made a corresponding molecule with a nitrogen in the middle. The homo /lumo gap will increase because the HOMO energy level is lowered while the LUMO stays the same. Thus, the most orbitals are stabilized by inclusion of the nitrogen.
Note that the orbital that has a node on the central atom is not affected by this change.
This is how molecular orbital theory helps you predict how the properties of molecules change with additions of particular atoms.
Pentadienyl Radical
If you consider the pentadienyl anion, radical and cation, that each has nodes on either odd or even atoms in the HOMO or LUMO and that the nodes do not match up in position. The middle orbital has the same energy as carbon. The gap between levels decreases more rapidly than for even numbered orbital molecules.
This is the basis for making some simple predictions about the spectroscopy of so-called cyanine-like molecules upon substitution of atoms along the chain with either electronegative or electropositive elements. Likewise the addition of electron donating and withdrawing groups can have similar effects.
Another distinction between cyanine-like dyes and polyene like dyes is the in polyene there is a complete reversal of the bond order between the π-bonding HOMO and the π-antibonding LUMO.
In contrast, in cyanines because typically either the HOMO or the LUMO is non-bonding, and because there are nodes at the atoms rather than between bonds in the frontier orbitals, there tend to be smaller changes in bond-length between the HOMO and LUMO. This will have spectroscopic implications. Anything that pushes electron density onto an atom increases the energy of the atomic orbital associated with that atom. Anything that takes electron density away will decrease the corresponding orbital energy.
| Previous Topic | Return to Molecular Orbitals Menu | Next Topic |