Difference between revisions of "Polarization and Polarizability"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| Line 42: | Line 42: | ||
If you plot dipole moment against the electric field you get a straight line. The slope (α) of the line for the function is the linear polarizability. A higher α means a greater amount of polarization for the same amount of applied field. | If you plot dipole moment against the electric field you get a straight line. The slope (α) of the line for the function is the linear polarizability. A higher α means a greater amount of polarization for the same amount of applied field. | ||
[[Image:polar_plot.JPG|thumb|400px|]] | [[Image:polar_plot.JPG|thumb|400px|The dipole moment is directly proportional to the applied field]] | ||
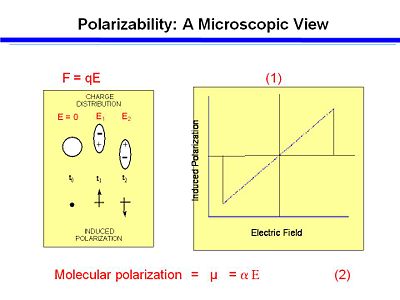
:<math>\mu = \alpha \Epsilon\,\!</math> | :<math>\mu = \alpha \Epsilon\,\!</math> | ||
Revision as of 12:17, 10 June 2009
| Previous Topic | Return to Molecular Orbitals Menu | Next Topic |
Polarization is an important concept in designing electro optical materials.
Mechanisms for polarization
If you have any mechanism to apply an external electrical field this may lead to polarization of the molecules. In electronic polarization the field pulls electrons more than it repells the nucleus because electrons are far lighter than the protons and neutrons. The timescale for polarization of a atom due to a field is 10 -15 seconds. This is about as fast as you can do things.
If two atoms with unequal electronegavity are bonded the molecule will have a dipole moment. A vibration of the atoms results in a change in the position of the nuclei and the electrons follow the nuclei. This happens on a timescale of picoseconds. Infrared leads to vibrations of molecules. The reciprocal of the frequency of IR has a time constant of 100 femptoseconds.
You can have molecules that already have a dipole moment and place them in an electronic field the molecules will align. This time constant for this rotation is in the area of 10s of nanoseconds. Microwave radiation can be used to cause rotations in molecules.
If there are ions in the presence of an electric field there will be a bulk motion. If there is an oscillating electronic field it needs to be matched to the timescale of the polarization mechanism. Only those components that react as fast or faster than the frequency will make a contribution to the bulk polarization of the material. The following animation demonstrates these four types. Click the switches to apply an electric field.
<swf width="500" height="400">http://depts.washington.edu/cmditr/media/01 Polarization Mechanisms.swf</swf>
Here is an hydrogen atom in an oscillating electric field. The atom is is oscillating as the electrons are being displaced and the energy levels are changing.
In an atom with π orbitals there is more polarizability in the π orbitals than in the σ orbitals. Dyes are typically π conjugated compounds because π orbitals are more polarizable in the visible spectrum.
Linear polarizability
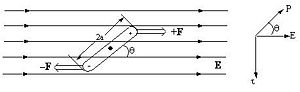
Molecules that have a dipole moment will orient in an electric field. These are known as second order non-linear materials. The force that is on the system is a torque that is related to angle between dipole and the electric field, and upon the magnitude of the field and the dipole. If the molecule is aligned with the field it will not feel a torque. If it oriented at 90 degrees it will feel a substantial torque.
Dipole is vector quantity, it has a magnitude and a direction. An opposite field will induce a dipole in the opposite direction.
If you plot dipole moment against the electric field you get a straight line. The slope (α) of the line for the function is the linear polarizability. A higher α means a greater amount of polarization for the same amount of applied field.
- <math>\mu = \alpha \Epsilon\,\!</math>
where
- <math>\mu\,\!</math> is the dipole moment
- <math>\alpha\,\!</math> is the linear polarizability, (slope of the line)
- <math>\Epsilon\,\!</math> is electric field
Anisotropic Polarizability
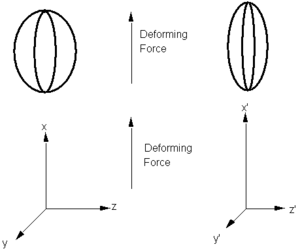
An organic molecule, 2-4 Hexadi-ine has two triple bonds and single bonds between two of the carbons. The triple bonds form a cylinder of electrons. If you apply and electic field along the long axis of the cyclinder you will get a larger induced dipole moment. If you assume that the polarizability at 90degrees to the axis is negible compare to the that of the along the long axis then electrons are going to move along the axis only. The interaction of the electric field with the electrons is greatest in long direction, and becomes zero at 90 degrees. This can be described as a dot product, a cosine function. An oscillating field will cause electrons to move up and down along the long axis and creates an induced dipole. Molecules that are oriented at 45 degree angle will have some induced dipole due to the applied field. This induced field can be used with cross polarizers to allow or not allow light to pass through the material.
Tensor calculation
To describe the polarizability of this kind of molecule you have to use a tensor to describe all the components of polarizability. It is possible to apply an electric field along y but induce a dipole moment along y. Each entry of the tensor is a component of the polarizability.
<math>\begin{pmatrix} \mu_x\\ \mu_y\\ \mu_z \end{pmatrix} = \begin{pmatrix} \alpha_{xx}& \alpha_{xy}& \alpha_{xz} & \\ \alpha_{yx}& \alpha_{yy}& \alpha_{yz} & \\ \alpha_{zx}& \alpha_{zy}& \alpha_{zz} & \end{pmatrix} = \begin{pmatrix} E_x \\ E_y \\ E_z \end{pmatrix} \,\!</math>
You can calculate the degree of polarization in any direction with the tensor product;
<math>\mu_x = \alpha_{xx} E_x + \alpha_{xy} E_y + \alpha_{xz} E_z\,\!</math>
Consider the electric field is a deforming force and the dipole moment is the deformation. The balloon can be stretched in one direction resulting in changes in the other dimensions. A balloon could be isotropic meaning it would be equally easy to stretch in all directions. Or it could have fibers built in that would limit the deformation along one axis. An electric field from any direction can induce a dipole in any direction. The components along the diagonal tend to be the strongest. It is possible to have more than one electric field applied (along x and y). To describe this situation you actually need a 3 x 3 x 3 (third rank) tenso, a matrix with 27 components. You could even have 3 electric fields with 81 components.
Dielectric Constant
We use the dielectric constant we often are referring to a solvent. A refractive index refers to speed of light. For a bulk material we describe the polarization density in a material. Instead of looking at a single molecule, we can look at the polarizability of the entire bulk material induced by an elecric field.
In bulk materials, the linear polarization is given by:
- <math>P_i(\omega) = \sum_{ij}\chi_{ij}(\mu)E_j(\omega)\,\!</math> (4)
where
- <math>\chi_i( \omega )\,\!</math> is the polarization density in direction i.
- <math>\omega\,\!</math> is the frequency
- <math>\chi_{ij}(\omega)\,\!</math> is the linear susceptibility of an ensemble of molecules.
Note that the vectorial and tensor aspects of E and <math>\chi\,\!</math> have been ignored to simplify notation.
The total electric field (the "displaced" field, D) within the material becomes:
- <math>D = E + 4\pi P = (1 + 4\pi \chi)E \,\!</math> (5)
- <math>P = \chi E\,\!</math> (Equation (4)),
- <math>4 \pi \chi E\,\!</math> is the internal electric field created by the induced displacement (polarization) of charges.
The Index of Refraction
The dielectric constant and the refractive index n(ω) are two bulk parameters that characterize the susceptibility of a material.
ε (&omega) in a given direction is defined as the ratio of the displaced internal field to the applied field (ε = D/E) in that direction.
- <math>\epsilon_{ij} (\omega) = 1 + 4\mu \chi_{ij} (\omega)\,\!</math> (6)
The dielectric constant of the material relates to the susceptiblity of the material, which relates to the polarizability of the molecules. Since $chi; is frequency dependent because of the different mechanisms that can induce polarization, then ε the dielectric constant is also frequency dependent.
The frequency dependence of the dielectric constant provides insight into the mechanism of charge polarization. with low frequency you can get contribution from electronic, vibronic, and rotational polarization. As you increase the frequency the dielectric constant drops until the point where the only contributing factor is the electronic polarization.
The ratio of the speed of light in a vacuum, c, to the speed of light in a material, v, is called the index of refraction (n):
- <math>n = \frac {c}{v}\,\!</math> (7)
Index of refraction is typically measured at low frequencies. At optical frequencies the dielectric constant equals the square of the refractive index:
- <math>\epsilon_\infty(\omega) = n^2(\omega)\,\!</math> (8)
Consequently, we can relate the refractive index to the bulk linear (first-order) susceptibility:
- <math>n^2(\omega ) = 1+ 4\pi \chi(\omega)\,\!</math> (9)
Index of refraction depends therefore on chemical structure. For example iodine has a higher index of refraction than fluorine because iodine is has a higher electron affinity, and therefore has more polarizability, so as material it has as a material greater susceptibility, therefore the refractive index is higher. This is a simple and essential factor of optics. As an organic chemist you can manipulate the atoms of a molecule to change the polarizability and thereby control the optical properties of the material.
Birefringence
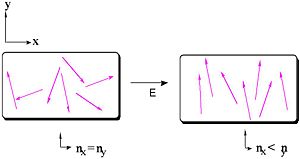
Isotropic molecules appear and behave the same regardless of their orientation. Anisotropic molecules have different properties depending on their angle.
Consider a material that is comprised of molecules that are dipolar and have polarizability anisotropy, then apply and electric field that couples with the dipole and induces a preferred orientation for the molecules:
An electric field can induce birefrignece. The molecules will have a different susceptibility, therefore a different polarization, therefore a different dielectric constant therefore a different index of refraction. Light that passes through a birefringent materials with one polarization will have a slower speed than the light with a different polarization. Consequently the light waves emerge at different times. Examples of birefringent materials include quartzite, quartz feldspar and potassium dihydrogen phosphate (KDP). This property is significant for non-linear optics and liquid crystals.
Classical Polarization
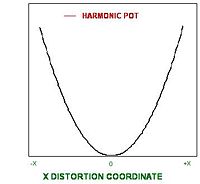
For linear polarizability, the electrons are bound to the atoms in a harmonic potential, i.e., the restoring force for the electron is linearly proportional to its displacement from the nucleus:
- <math>F = -\Kappa x\,\!</math> (10)
The electrons see a potential energy surface:
- <math>V = 1/2 \Kappa x^2\,\!</math> (11)
The force is the derivative of the potential energy. This means that there is a symmetrical distribution of electron density around the atom with an equal ease of charge displacement in both the +x and -x directions. The extent of polarization if linearly relate to the applied field.
- <math>P_{ind} = \alpha E\,\!</math>
Applying an Oscillating Electric Field
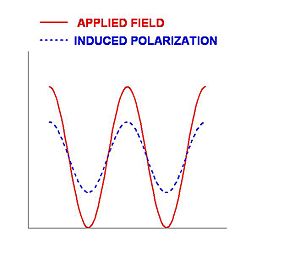
Application of an oscillating electric field will induce an oscillating polarization in a material. For linear polarizability, the polarization will have the same frequency as the applied electric field. If a sinusoidal wave field is applied the induced field will be sinusoidal. It may not have the same amplitude as the applied field but it will follow it. Light is an oscillating electromagnetic field. This induced polarization is itself a source of light which will propagate through the material in the same direction and with the same frequency as the light beam that created it. Because the electrons respond linearly to the applied field the induced wave is similar to the applied wave. However they the two waves may not have the same phase because it takes time for the electrons to move during induction process.
During the process there is no net transfer of energy to the material. However if the frequency of light approaches the natural resonance of the molecule it is possible to transfer to energy to the molecule giving it an excited state, or producing heat or other chemicial reactions.
| Previous Topic | Return to Molecular Orbitals Menu | Next Topic |