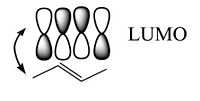The Polyene Series

Now we will explore the electronic properties of the polyenes; methylene, ethylene, butadiene etc. Photonic properties of the polyene series can be generalized as we start with simple molecules and construct longer and longer chains.

Methyl radical

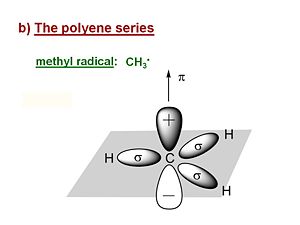
The Methyl Radical

Its useful first to look at the methyl radical CH₃·. It has a planar structure with the carbon and three of the four valence in the plane. The hydrogens are in σ orbitals which are symmetrical about the plane of the bond. The unpaired electron or radical is in a 2p_z atomic orbital that is perpendicular to the plane of the molecule. The π AO for that radical has a lobe above the plane, and a negative lobe below the plane. The probability of the electron is always zero at the nucleus. The lobes in the diagram represent the surface within which there is an 80% probability of finding the electron.

Relative energy of π and σ orbitals

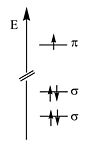
The energy of the π electronic orbital is much higher than the σ orbitals. All of the optical and electrical properties of the polyenes are due to highest occupied molecular orbitals which are the π orbitals.

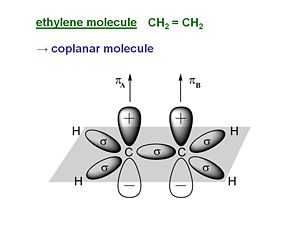
Ethylene

Ethylene molecular orbital

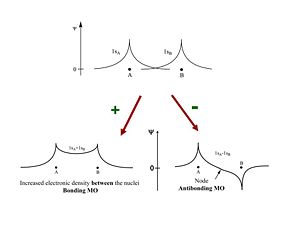
Ethylene is π- conjugated molecule. It can be thought of as two methyl radicals coming together and losing two hydrogens. It is coplanar molecule with a σ bond between the carbons. Each carbon has a π- electron orbital that overlaps with the other because the carbons are close. In a perfectly planar system the π- electrons will not interact with the σ bond. But as soon as the molecular becomes non coplanar there can be interaction.

Homo / Lumo diagram for ethylene

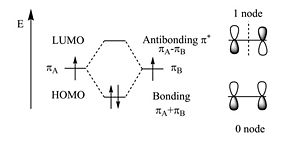
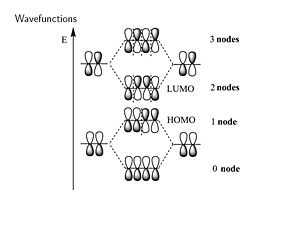
Two π wavefunctions with the same sign form a bonding molecular orbital with a higher density between the carbon nuclei (no nodes). If the signs are different an antibonding orbital with a node between the nuclei forms. From a methyl radical like π atomic orbital contribute two π electrons in to the bonding molecular orbital which will be the highest occupied molecular orbital (HOMO). The antibonding π * (* denotes unoccupied) corresponds to the lowest unoccupied molecular orbital (LUMO). The energy difference between HOMO and LUMO is 7ev. This is the energy that would have to be supplied by a photon to bring promote an electron to the LUMO level. The visible part of the EM spectrum is between 1.5eV and 3eV. So the first optical transition occurs above the visible spectrum.

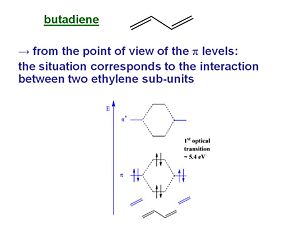
Butadiene

Butadiene Energy Levels

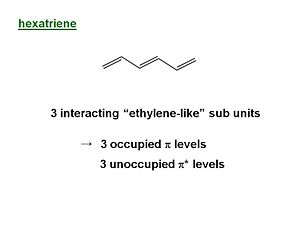
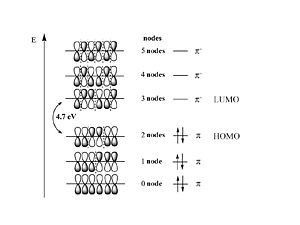
From the point of view of the π level butadiene corresponds to the interaction between two ethylene sub-units. The π homo level of one ethylene subunit interacts with the π homo level of the other subunit. There can be a positive combination and a negative combination, one leads to a level that is more stable one that is less stable. The same thing happens for the π* levels. The π * LUMO has come down while the π HOMO has increased. As a result the energy difference between HOMO and LUMO (the first optical transition ) has decreased to 5.4 eV.

Butadience wavefunctions

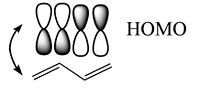
Considering the wavefunction. The positive combination gives you all bonding for the lowest π bonding orbital. Then mixing two positive with two negative (++--) you fill the HOMO level resulting in a single node. In the π * orbitals the LUMO includes a negative combination (+--+) which results in bonding in the middle with 2 nodes. The fully antibonding molecular orbital has three nodes.

The bonding – antibonding character of the HOMO wavefunction translates to the double-bond / single-bond character of the geometry in the ground state. Higher electron density in the π MO corresponds to the double bond that allows the nuclei get closer (shorter bond length), lower density in single bond corresponds to the node between the antibonding orbitals.

Butadience Bonding and Antibonding- HOMO

Butadience Bonding and Antibonding- LUMO

Hexatriene

Hexatriene has three ethylene like sub units, 3 occupied levels and 3 unoccuppied pi * levels.

Hexatriene wavefunctions. The wavefunctions for hexadiene can have 0, 1, or 2 nodes in the HOMO. The gap between the HOMO and LUMO is 4.7eV.

The smoother the evolution of the wavefunction the smaller the kinetic energy term that is associated with it.

The energy of the π MO’s goes UP as a function of the # of nodes this is related to the kinetic term in the Schrödinger equation.

<math>\hat{H}\rightarrow \hat{K} + \hat{V}\,\!</math>

<math>

\hat{K} \rightarrow (\frac{ \partial} {\partial x^2}+ \frac{ \partial} {\partial y^2} +\frac{ \partial} {\partial z^2})\,\!</math>

Geometry

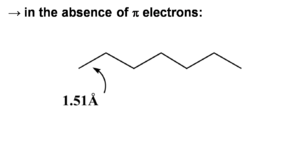
In the absence of pi electrons all of the C-C bond lengths would be nearly equal (about 1.51Angstrom for sp2 bonds).

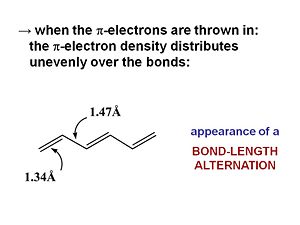
When π electrons are added they will be distributed unevenly over the bonds. The double bonds are shortened (1.34 A). Even the single bond will be shorter (1.47 a) than a single bond because of the π conjugated system. The HOMO wavefunction reflects the single double bond alternation in the ground state. If we add an electron to hexatriene (reduce it) this electron will go to the LUMO causing an antibonding factor between the first carbons. This will cause the first bond to lengthen. So a rule of thumb is that when an electron is added to an antibonding wavefunction the bond will elongate. If it is added to a bonding factor then it will shorten.

Going the ground state geometry to the reduced state there is lesser degree of bond length alternation because double bonds will have lengthened and the single bonds will have shortened. When the molecule is oxidized(remove an electron) the electron is lost from the HOMO, that is from a bonding factor, it weakens the bonding characteristic and that bond will elongate. But if the electron is removed from an antibonding wavefunction, that allows the bond to shorten. As a consequence adding an electron on the LUMO (i.e. reduce the molecule) or removing an electron from HOMO (oxidize the molecule) the double bonds will elongate and the single bond will shorten. When going to the excited state (taking and electron from the HOMO to the LUMO) there should be longer double bonds and shorter single bonds compared to the ground state. This is because the π electron densities on the bonds changes the geometry of the molecule.

Chain size

The electron band structure of polyacetylene.

The energy of the first optical transition (π to π* or HOMO to LUMO) decreases in conjugated chains approximately as 1/n where n = number of atoms. The plot of energy vs n is linear.

The energy difference between consecutive π (π* levels) levels becomes smaller and smaller as the chain gets longer. At the limit of an infinite chain the change between levels is infinitely small. This results in continuous energy zones for the π levels and for the π* levels leading to energy bands.

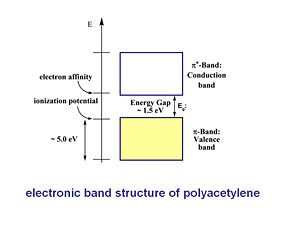
Electronic Band Structure of Polyacetylene

The π band is referred to as the Valence band and the π* is called the Conduction band. This a assumes a perfectly coplanar chain. The width of the Valence band and the Conduction band is about 5eV. The energy gap or band gap E_g is about 1.5eV, this also known as the ionization potential. The bottom of the Conduction band is also known as the electron affinity. With trans polyacetylene and other conjugated polymers the picture must be refined because of the connection between the geometries and electronic properties.