Interchain Interactions
| Previous Topic | Return to Absorption and Emission Menu |
Interchain interactions is an important consideration with light emitting polymer and oligomers.
Photoluminescence is easily measured by shining light and measuring the emission. In dilute solutions or inert matrices the photoluminescence quantum yield of a given conjugated polymers can be very large: up to 60-80 %. However these substances are much more useful if they can deployed as thin films.
But in thin films the solvent goes away, the polymer chains get closer so they can interact and the luminescence can be nearly totally quenched. The observation of quenching led researchers to explore the cause and remedy for this. (Note: There are a few situations where going from solution to solid states you can get increased luminescence. Silos for example can cause an aggregation in the solid state that triggers luminescent qualities.)
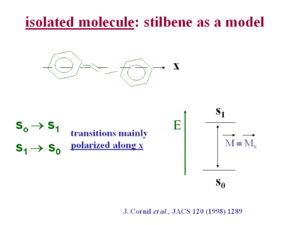
Transition dipole in isolation
A transition dipole is directly related to the probability of a transition occurring from one excited state to the ground, or the ground to the excited state. It is also related to the intensity of the exciting energy.
If the wave function for the S1 state is localized in a different area of space than the ground state then transition dipole will be zero. There must be wave function overlap for the wave function equation to be non-zero.
In stilbene the transition dipole for the S0 → S1 transition and the S1 →S0 transition is polarized mainly along the long axis (x axis) of the molecule. This is generally the case in pi conjugated systems because as you extend the length of the chain electrons are delocalized over a longer distance, just as in an electrostatic dipole a larger distance of charge separation make for a larger dipole moment. An exception is pentacine whose first optical transition is polarized at 90 degrees from the long axis of the chain. In most other optical polymers such as polyvinylene and polythiophene the optical transition is polarized along the long axis.
see Cornil [1]
Two chain interaction
When two chains come into close proximity they there is the possibility during excitation the electron will jump from one chain to another, leaving a hole and forming a charge transfer exciton. The probability of finding h+ and e- on separate chains in S1 can be obtained from the excited-state wave function .
S1 → S0 intensity can go down since the transition is polarized along x.
Symmetrical interaction
Consider first the most symmetric configuration which is perfectly cofacial.
From a distance of infinity down to 8 Å there is no significant interaction. There is no significant wave function overlap between the units.
- excitation is always localized on a SINGLE UNIT
- PL is not affected
This is the situation in dilute solution or inert matrices
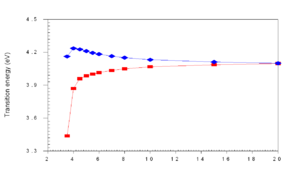
When the distance (R) drops below 8 Å , as they do in thin films, the wave functions of frontier orbitals (homo and lumo) begin to overlap and you get a new splitting of the homo level. Wavefunctions are delocalized over the two units. They become equally spread in the zone of r~5 Å.
Exciton band formation
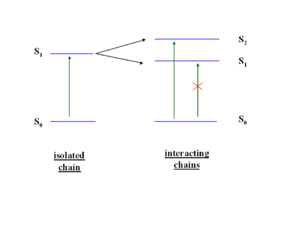
The HOMO and LUMO may be split to different degrees. In a highly symmetrical situation the transition from the ground state to the lowest excited state (S1) is forbidden. The HOMO (au) and the LUMO (bu) is are both ungerade which means the transition is forbidden (because odd time odd is even, times odd is odd and when this is integrated over all space the result is zero).
If you were able to stack five molecules on top of each other, you could have five excited states corresponding the mixing of the five states corresponding to the five S1 states, this is known as an exciton band. Even if a higher excited state such as S2 is achieved, Kasha’s Rule dictates that energy will relax down to lower states and the emission can only occur from the lowest excited state. S1 can not transition to S0, it is a “dark state” .The lowest state of that exciton band will be dark and luminescence is quenched.
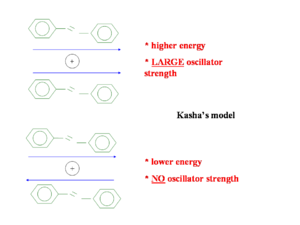
Kasha’s model from goes back fifty years and attempts to explain the emission from the lowest state. He only considered the wave function of one molecule interacting with that of another molecule. He did not consider mixing of wave functions so a charge transfer state with an electron on one molecule and a hole on another is impossible in his model. The diagram shows two molecules with transition dipoles along the main axis of each, one dipole parallel and the other anti-parallel. When the two dipoles are opposing the energy is less than the parallel situation but the oscillator strength is zero. In the parallel situation the oscillator strength is large and but the energy required to get there is higher.
So when two transition dipoles interact, the two S1 states split forming a two state exciton band with S1 and S2. The lower ground state S1 is most favorable because it formed by the antiparallel orientation of the transition dipoles. The S2 has a high oscillator strength (its bright) but higher energy, S1 is lower energy but has low oscillator strength (its dark). So in the highly symmetrical situation molecule interact and illumination is quenched.
As molecules get closer and closer (approaching 4 Å) in cofacial configuration their wave functions interact and there is a splitting into S1 and S2. This results in a blue shift of the absorption because the molecule has to get up to the higher S2 state since S1 is not optically coupled with the ground state.
Geometry relaxation effects
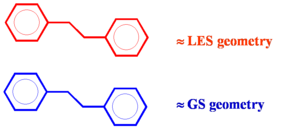
If a conjugated system goes into an excited state there will be geometry relaxation. Considering two molecules one on top of another there will be unequal relaxation. In the this case the top molecule achieves lowest excited state (LES) geometry while the lower molecule stay in ground state (GS) geometry. Excitation into S2 trickles down to S1 state and then localizes on one of the molecules. The two molecules do not have the same geometry and the system has less symmetry. This asymmetric geometry deformations allow it to break the selection rules. Thus relaxation allows for a little bit of electronic coupling and some emission.
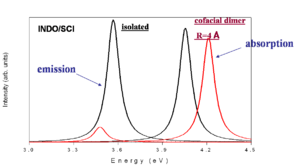
This is a simplified depiction of the spectra that are found experimentally. The black curves represent the isolated molecules. The molecules absorb at a higher energy and emit at a lower energy (emission is redshifted with respect to absorption). When there is cofacial dimer (R= 4 Å) there is blue shift of absorption because the you can only go to S2. If there is no geometry relaxation in the excited state there will be no emission. With relaxation on one molecule there will be reduction of symmetry and some emission that is red shifted with respect to the emission in the isolated system.
The larger the transition dipole ( meaning larger oscillator strength, larger electronic coupling) the shorter the excited state lifetime. Strong coupling means there is a high probability that the transition will occur and there will be higher quantum yield. Probability determines the time in the excited state. The longer the molecule stays in the excited state the higher the more time for the system to find vibrations that will allow it to go back to the ground state by other means such as non-radiative decay. This results in a decrease in luminescence quantum yield.
For example there is electron transfer that can take place between PPVm derivative and fullerene C60 that occurs in 35 femptoseconds. That is so short that nothing else can occur. In that case electron transfer has 100% quantum yield. In general the process that is fastest that is the one that will dominate all others.
References
- ↑ J. Cornil et al., JACS 120 (1998) 1289 doi:10.1021/ja973761j
| Previous Topic | Return to Absorption and Emission Menu |