Gold Nanoparticles – Surface Plasmon Resonance
The Fates of Excited States of Organic Dyes on Gold Nanoparticles
Contributed by Michal Malicki - Georgia Tech- Thesis Introduction
Gold Nanoparticles – Historical Perspective
Metal nanoparticles show very interesting optical properties. The use of these miniscule objects for glass staining dates back to the ancient times. “Ruby glass”, which is essentially glass containing gold nanoparticles, has been used since antiquity until the present. A classic example of an ancient piece of art gaining its appeal from the color produced by metal nanoparticles is the late Roman “Lycurgus Cup”, which is exhibited in the British Museum.[1] Depicting the mythological scene of Lycurgus’s entrapment by the vine-turned Ambrosia, a maenad of Dionysus, the cup shows extraordinary dichroic behavior exhibiting red color in transmission and green color in reflection (see Figure 1). This beautiful effect is due to absorption and scattering of gold and silver nanoparticles which are present in the glass from which the cup is made.[2][3]
A revolution in the use of gold metal for glass and ceramic staining did not take place until late 17th century when it was discovered that combining aqua regia solution of gold and tin produces a precipitate with deep and vibrant red color.[4] Named “purple of Cassius”, after its alleged inventor, the colorant became one of the most successful red pigments used in the production of glass and ceramics, and it is still in use today.4,5, Even though Andreas Cassius had been given the credit of the discovery and the 1685 recipe of the “purple of Cassius” he was not the first to discover the recipe for the preparation of the famous colorant. By 1659 a report of the preparation of the red pigment had already been published by Johann Rudolf Glauber, and by about 1679 the colorant had been in use in a glass factory at Potsdam. The history of this is rather fascinating as there were apparently two persons named Andreas Cassius – a father and the son to whom the discovery of “purple of Cassius” was attributed – and it is not clear what the role of each one of them was in the development of the dye. More on this can be found in Ref.(5)[5].
Apart from their use for staining glass and ceramics, gold particles were also employed in photography. In 1842 Sir John Herschel developed his “chrysotype” process in which a photochemically reduced iron(II) salt was exposed to a tetrachloroaurate(III) salt, resulting in the reduction of gold(III) to gold(0), with subsequent formation of gold particles.[6] Even though this method did not survive competition from the silver photography invented earlier by Talbot, gold particles were successfully and routinely used for toning silver photographs, which gave them increased stability.[7]
Much work in the early days of chemistry was stimulated by the “purple of Cassius”. The question of the composition and nature of the dye constituted a serious, often raucously argued, scientific problem in the 19th century. The first time it was recognized that “purple of Cassius” is composed of “extremely finely divided gold” was in 1802. This was published by Jeremias Benjamin Richter, the same chemist who bequeathed us the law of definite proportions. A number of historically famous chemists took part in the discussion – Joseph Proust, Jöns Jacob Berzelius, and Joseph Louis Gay-Lussac, just to name a few. The main argument in those days revolved around the question whether the gold in “purple of Cassius” is in the form of an oxide or in its metallic form.4 In the contemporary literature the moment considered as the definitive recognition of gold particles as the main constituents of “purple of Cassius” seems to be the Bakerian Lecture Michael Faraday gave to the Royal Society in 1857.7 Faraday devoted a part of his scientific career to studying the interactions of “finely divided” metals, especially gold, with light by which, as his writing implies, he was fascinated. It is captivating to read about his motivation to study the metal particles in the context of these interactions. Being an exceptional experimentalist, Faraday intuitively felt that experiments with highly absorbing metal particles with sizes smaller than the wavelength of light may give useful insights supporting the theory of ether, which he accepted.7 Though the legacy of Faraday’s work obviously does not include a proof for the existence of ether, the body of his work on the interaction of metal particles with light marks the beginning of modern spectroscopy research on colloidal gold.3,8
It is important to add that the discussion on the composition of “purple of Cassius”, which animated the scientific discourse in the 19th century, found its definitive conclusion in the work of Richard Zsigmondy reported in 1898.9 The Hungarian-born chemist used his invention – the ultramicroscope – to show that the red color in “purple of Cassius” comes from tiny gold particles – colloidal gold.4,9 In 1925 he was awarded the Nobel Prize in chemistry “for his demonstration of the heterogeneous nature of colloid solutions and for the methods he used, which have since become fundamental in modern colloid chemistry”.10
A mathematically rigorous description of the color of gold particles was demonstrated at the beginning of 20th century in terms of classical electromagnetic theory. James Maxwell Garnett and Gustav Mie independently described the interaction of metallic nanoparticles with light and rationalized the observed nanoparticle colors using classical electromagnetism.11-13 This purely classical description of light absorption and scattering by metal nanoparticles still dominates today and is a source of fruitful scientific findings.3,8,14,15
Not to downgrade numerous research activities throughout the 20th century, but one late report appears to be an important milestone in the gold nanoparticle research. Published by Brust et al. in 1994, it described a successful preparation of gold nanoparticles in organic solvents with the use of organic thiols as stabilizers of the resulting colloidal gold.16 This started a renaissance in gold-nanoparticle research as the organic-soluble particles could be treated like typical organic compounds; i.e., standard organic chemistry techniques could be used for the manipulation of these species. Additionally, the synthetic accessibility and flexibility of the organic-thiol stabilizers made it possible to systematically study a variety of effects of the stabilizer molecules on the physical properties of the gold particles and vice versa.
Gold Nanoparticles – Surface Plasmon Resonance
A prominent spectroscopic feature of noble metal nanoparticles (NPs) is the so-called surface plasmon resonance, which gives rise to a sharp and intense absorption band in the visible range. The physical origin of the absorption is a collective resonant oscillation of the free electrons of the conduction band of the metal.8,14,17 Figure 2 shows a representation of the displacement of the conduction-band electrons induced by a resonant incident electric field.
For a spherical nanoparticle that is much smaller than the wavelength of the incident light its response to the oscillating electric field can be described by the so-called dipole approximation of Mie theory.8,15 In this approximation the wavelength-dependent extinction cross section of a single particle, Cext(λ), which defines the energy losses in the direction of propagation of the incident light due to both scattering and absorption by the particle, is described in terms of the dielectric function of the metal, ε(λ) = ε'(λ) + iε(λ), and the dielectric constant of the medium, εm, as shown below:15 For gold nanoparticles smaller than 60 nm the scattering cross section is negligible when compared to the absorption cross section. (18)Hodak, J. H.; Henglein, A.; Hartland, G. V. J. Phys. Chem. B 2000, 104, 9954-9965.
- <math>C_ext (\lambda)=\frac {24 \pi ^2 R^3 \varepsilon _m^{3/2}} {\lambda} \frac {\varepsilon ^{} (\lambda)} {(\varepsilon ^{'} (\lambda )+2\varepsilon _m )+\varepsilon ^{} (\lambda )^2} \,\!</math> Equation 1
where
- <math>\lambda\,\!</math> is wavelength of the incident light
- <math>R\,\!</math> is the particle radius.
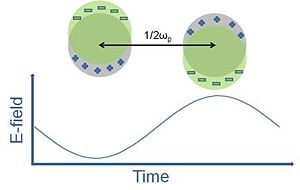
As can be seen from Equation 1, the extinction cross-section of a particle depends on the dielectric function of the metal of which the particle is composed. This gives rise to very different absorption and scattering characteristics for different metal nanoparticles. The maximum of Cext(λ), or the resonance condition, will take place when the denominator of the right-hand side of the equation becomes minimal. This is fulfilled approximately at the wavelength λp for which ε'(λp) = -2εm, if the imaginary part of the metal dielectric function, ε(λp) is small.8,15 The frequency of the surface plasmon resonance, ωp, is then observed at ωp = c / λp where c is the speed of light in the medium. The frequency of the surface plasmon resonance, ωp, is depicted in Figure 2 in terms of the period of the oscillation of the electric field and the conduction electrons within a metal nanoparticle. Mie theory and its dipolar approximation in the case of small particles can be successfully used to calculate extinction spectra of metal nanoparticles. Using an experimental determination of the dielectric function of the bulk metal and the particle radius, calculations based on Equation 1 yield extinction cross section often in excellent agreement with measured absorption spectra of the corresponding nanoparticles.17
The resonance condition implies that the surface plasmon resonance frequency depends heavily on the dielectric constant of the medium, εm. Indeed, the color of colloidal gold changes with the dielectric constant of the solvent. Underwood and Mulvaney demonstrated that effect by measuring UV-Vis absorption spectra of polymer-stabilized gold nanoparticles of 16 nm in diameter in a series of solvents with different refractive indices. The authors showed that a change in the solvent refractive index from 1.30 to 1.60 lead to a shift in the measured maximum of the surface plasmon resonance band from 520 nm to 545 nm. Additionally, the measured positions of the maxima agreed perfectly with the values calculated with the use of Mie theory.14
From the perspective of a chemist it is interesting to ask how the absorption efficiency of gold nanoparticles compares with that of typical organic dyes. After all, the collective oscillation of the conduction band electrons in metal nanoparticles that gives rise to the surface-plasmon absorption band is a rather exotic concept to a chemist when put side-by-side with an absorption process in typical organic dyes, which often can be well-described as a one-electron transition between two molecular orbitals. Comparing experimentally determined molar extinction coefficients for gold nanoparticles with extinction coefficients of well-known dyes shows just how much more efficient an absorber a nanoparticle is when compared to an organic dye. As can be seen in Table 1, even for rather small nanoparticles (ca. 4 nm in diameter) the molar extinction coefficient is almost two orders of magnitude larger than that of Rhodamine B, which is considered to be an efficient absorber.
Table 1. Experimentally measured molar extinction coefficient values, ωM, of selected organic dyes at their absorption maxima, and of solutions of gold nanoparticles with different diameter, D, at the maximum of the surface plasmon resonance band. Values for the organic dyes were taken from ref. 20 and data for Au NPs were taken from ref. 21.
Solutions in: a - cyclohexane, b - ethanol, c - toluene, d - water
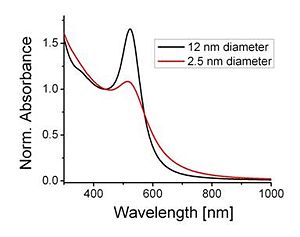
The molar extinction coefficient of gold nanoparticles increases roughly cubically with the particle radius reaching impressive values on the order of 108 L (mol × cm)-1 for particles larger than 20 nm.21,22 The cubic dependence of the experimentally measured molar extinction coefficient on the particle diameter is in agreement with Mie theory (see Equation 1),22 and it is a manifestation of the collective oscillation of the electrons in the nanoparticle, since the total number of electrons within the nanoparticle depends on its volume and, thus, on the third power of the diameter. Figure 3 shows absorption spectra of oleylamine-stabilized Au NPs in toluene solutions. As can be seen from the graph the most prominent feature in the spectra of two sets of particles with different diameter is the band around 520 nm, which is a manifestation of the surface plasmon resonance. The spectra were normalized at 450 nm, at which wavelength the majority of the absorption signal comes from the interband transitions of the metal.23 Presented in such way the spectra show that the surface plasmon resonance band is much more pronounced and sharper for large particles (12 nm diameter) than for smaller particles (2.5 nm diameter), qualitatively consistent with the discussion above.
Gold Nanoparticles – Surface Plasmon Resonance Dynamics
The large absorption cross-section values of the surface-plasmon resonance band imply that a NP is able to efficiently acquire a vast amount of energy when irradiated with light at the appropriate wavelength. Thus, it is interesting to ask questions about the excited-state deactivation pathways and their corresponding dynamics in gold nanoparticles. In other words, how efficient is the deactivation of a photoexcited gold nanoparticle? It is useful to clarify what is meant by excited-state deactivation in the context of the surface plasmon resonance in metal nanoparticles. Because the surface plasmon resonance is a manifestation of a coherent oscillation of the conduction band electrons, the loss of coherence is a form of deactivation of the excited state and it may have observable effects. However, this loss of coherence does not involve any energy redistribution, but merely the change of the plane in which each electron oscillates (i.e. the change of the plasmon wave vector), thus leading to the loss in coherence. This process is very fast, on the order of a few femtoseconds. More on this can be found in Ref.(8)[8] We are instead interested in the deactivation of the NP excited state via energy dissipation and the discussion in this section focuses on this process only.
Emission of a photon is one of the pathways of energy dissipation in Au NPs. The efficiency of this process is, however, rather low. Dulkeith et al. demonstrated that gold nanoparticles exhibited a luminescence quantum yield of ca. 0.0001 %, independent of the particle size within the investigated range from 2 nm to 35 nm.24
A second process responsible for the equilibration of the photoexcited electrons in the Au NP after photoexcitation is electron-electron relaxation. The high-energy electrons after the photoexcitation can undergo collisions with other electrons present in the volume of the nanoparticle, leading to the partition of the energy between the electrons. This process leads to a change in the energetic distribution of electrons from the highly non-thermal distribution present immediately after the photoexcitation to a statistical Fermi-Dirac distribution with a high-temperature Fermi level.Sun et al. found experimentally that in bulk gold this thermalization process is ultrafast, reporting a time constant of ca. 0.5 ps.26
Since the particle is metallic, there is essentially a continuum of states available for the electrons and it is useful to talk about the electrons in terms of their kinetic energy / temperature. However, this is true only for particles larger than roughly 2 nm, as for particles with smaller sizes the molecular-like behavior starts dominating and size-induced gaps appear in the density of states of these systems. More on this can be found in the work of Prof. El-Sayed and Prof. Whetten and their research groups at Georgia Tech. For example see Ref. (25)[9]
The “hot electrons” further lose their kinetic energy due to collisions with the ionic crystal lattice of the NP. This process, usually referred to as electron-phonon relaxation, leads to the lowering of the Fermi level and thermalization of the crystal lattice of the nanoparticle.8 Hodak et al. showed that the electron-phonon-relaxation time constant in gold NPs did not depend on the size of nanoparticles for samples within the 2.5 nm to 120 nm size range,18 and that its value (ca. 0.7 ps) was very similar to that measured for bulk gold films.26 Since higher laser power causes a higher temperature jump of the electrons after electron-electron relaxation the electron-phonon-relaxation time constant depends on the power of the excitation beam, as shown experimentally by various researchers.8,18,22 A spectacular phenomenon related to the heating of the crystal lattice of gold NPs due to the electron-phonon relaxation has been demonstrated by Hodak et al.27 The researchers observed coherent oscillations in the signal of the surface-plasmon-resonance-band bleach in a femtosecond transient absorption experiment. The oscillations showed a frequency of ca. 6 cm-1 and coherence time of ca. 15 ps, which was limited by the polydispersity of the sample. The authors attributed the observed phenomenon to a vibrational “breathing mode” of gold nanoparticles with the hot lattice induced coherently by the photoexcitation followed by electron-phonon relaxation.27 The expanding – shrinking lattice of a nanoparticle causes shifts in the surface plasmon resonance band, thus causing the measured bleaching signal to show an oscillatory behavior.8,27
The final process that leads to the equilibration of a gold nanoparticle after the photoexcitation with the surroundings is sometimes called “phonon-phonon relaxation”. This process is responsible for the energy exchange between the hot crystal lattice of the nanoparticle with the surroundings. Dependent on the nature of the matrix in which the nanoparticles are embedded, the phonon-phonon relaxation time constants are usually on the order of tens to several hundreds of picoseconds.8,28 The time constant for this process does not depend on the excitation beam power (i.e. on the initial electron temperature after photoexcitation), but it depends on the square of the radius of the particles, which is in agreement with it being a mechanism of energy transfer through the nanoparticle surface.28
As described above, the rather complicated cascade of processes leading to the excited-state deactivation of gold nanoparticles is mostly non-radiative, implying fast and efficient heating of the close surroundings of the nanoparticle right after photoexcitation. This heating can be so efficient that it can actually cause irreversible changes in the nanoparticle morphology due to melting. This behavior has been exploited for a variety of potential applications including information storage,29 and cancer diagnostics and therapy.30
Noble Metal Nanoparticles – Local Field Effects
The induced collective electron oscillations associated with the surface plasmon resonance give rise to induced local electric fields near the nanoparticle surface. The induced electric field originating from the charge separation in the nanoparticle during the plasmon resonance oscillations is very large at very small distances from the surface. For silver nanoparticles the values of the induced field can be tens of times larger than the incident electric field values. Hao and Schatz performed calculations for a silver sphere with a 20 nm diameter and found that due to the surface plasmon resonance the incident electric field is enhanced by ca. 13 times at the immediate particle surface.31 This enhancement factor quickly drops to smaller values as the distance from the surface increases.31,32 These enhanced local fields are responsible for increased rates of field-dependent processes at surfaces of nanostructured metals.
While phenomena in which the local field effect plays a crucial role include surface-enhanced photochemistry33 and second-harmonic generation,34,35 perhaps the most celebrated analytical technique based on the local electric-field enhancement by metal surfaces is Surface-Enhanced Raman Spectroscopy. Jeanmaire and Van Duyne found in the late 1970s that pyridine molecules physisorbed onto a rough silver electrode exhibit an unusually strong Raman signal.36 It is agreed today that the enhanced intensity of the Raman scattering signal of molecules adsorbed on rough metal surfaces is largely due to the enhanced local field effects in the close proximity of the nanostructured metal surface. These signal enhancements can be as large as 1014, of which a factor of 107 - 108 is attributed to the local field effects.37,38 The large improvement in the detectability afforded by the signal enhancement resulted in a number of analytical techniques, including methods allowing one to probe single molecules.37,38
Wenseleers et al. demonstrated that two-photon absorption (TPA) induced fluorescence of an organic dye underwent very large enhancements when the dye was deposited onto a surface composed of silver islands with a fractal geometry.39 The authors rationalized this behavior in terms of the presence of so-called hot-spots on the surface of the silver film, at which the local field enhancements could be as large as 1.6 × 105. The local field effects on TPA were also demonstrated by Cohanoschi and Hernandez. They used Z-scan measurements to show that combining an organic dye in solution with aggregates of gold nanoparticles resulted in an enhancement of the TPA cross section by a factor of 480 times.40
The potentially important consequences of the enhancements in nonlinear spectroscopic response of molecules due to the proximity of metallic nanostructures form one of the points of motivation for the work on gold nanoparticles presented in this thesis.
Gold Nanoparticle / Organic Dye Systems and their Photophysics
The unique photophysical properties of gold nanoparticles, which include the efficient absorption characteristics and the local field effects discussed in the previous sections, offer many opportunities for sensing, photothermal, or nonlinear-optical applications. In addition, combining the properties of gold nanoparticles with those of known organic dyes has already led to interesting applications including mercury sensing,41 and sensing of biologically relevant molecules.42,43 Because of their chemistry, gold nanoparticles are an excellent platform for studying the influence of a metallic core on organic dyes in close proximity to it.
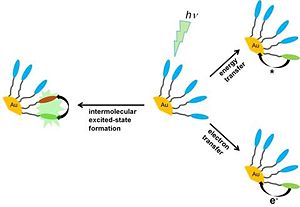
To date there are numerous reports on the study of the influence of gold nanoparticles on the photophysics and photochemistry of organic dyes anchored to the nanoparticle surface. The scientific questions dominating the developments in this field are related to the radiative and non-radiative deactivation pathways of the excited state of organic dyes immobilized on the surface of nanoparticles. Considering the geometry and photophysical properties of gold nanoparticles, three major processes leading to the deactivation of a photoexcited dye in close proximity to the nanoparticle surface should be considered. First, the efficient absorption by gold nanoparticles throughout the UV-Vis spectrum (see Figure 3) can lead to a fast energy transfer from the photoexcited dye to the nanoparticle. Related to the energy transfer is the modification of the natural luminescence lifetime, or radiative rate, of dyes by the proximal gold nanoparticle.44 Second, the photoexcited dye can undergo an electron transfer to the continuum of energy levels in the metallic core. Finally, the high local density of organic dyes anchored to the nanoparticle surface facilitates dye – dye interactions, which can manifest themselves through the formation of intermolecular excited species such as excimers.45 Figure 4 shows a schematic of the three possible mechanisms of deactivation of excited states of organic dyes by gold nanoparticles. Another process, not shown in Figure 4, that can play a role in the excited-state deactivation of dyes in close proximity to gold nanoparticles is connected with the change of the natural fluorescent lifetime, or radiative decay rate, of fluorophores and it will be discussed later on.44
Energy Transfer to the Nanoparticle and Radiative Rate Modification
Energy transfer from fluorescent organic dyes to gold nanoparticles is generally considered to be the major process leading to the excited-state deactivation of the dyes.45 Before introducing examples of published reports on the energy transfer involving gold nanoparticles, it is useful to discuss the mechanisms by which the process is likely to occur. Perhaps the most familiar mechanism is that of energy transfer via dipole-dipole interactions. Named after the scientist who described the mechanism mathematically, the rate of Förster resonance energy transfer (FRET) from an energy donor to an energy acceptor, kFRET, depends on: the fluorescence quantum yield of the donor, φDfl; its excited state lifetime,τD; refractive index, n; the distance between the donor and the acceptor, rD-A; and the spectral overlap of the fluorescence of the donor, fD(ν) with the molar extinction coefficient of the acceptor, εA(ν). The rate constant is described by the following equation:17
- <math>k_{FRET}=\frac {c \phi _{D} ^{fl} k^2} {n^4 \tau_D r_{(D-A)}^6} \int^{\infty}_{0} f_D (\nu) \varepsilon_A (\nu)\frac {d\nu}{\nu^4}\,\!</math> Equation 2
where c is speed of light, k is an orientational factor defining the projection of angles between the transition dipole moment of a donor and that of an acceptor, and \nu is frequency. As already mentioned, the fact that gold nanoparticles have very large molar extinction coefficients makes them potentially excellent energy acceptors, according to Equation 2. A sizeable effort has been directed at studying promising fluorescent energy donor – gold nanoparticle systems in order to understand the process of energy transfer in these hybrid systems.
Aguila and Murray showed that the fluorescence of dansyl cadaverine – a green-fluorescent dye – attached to the surface of small gold nanoparticles (1.6 nm in diameter) is quenched with respect to isolated dyes in solution.46 The authors reported that the intensity of the fluorescence emission of the dye attached to the nanoparticles is two orders of magnitude less intense than the fluorescence of the free dye at same concentration.46 This behavior was explained in terms of energy transfer from the photoexcited fluorophore to the metallic core of the gold nanoparticle. Additionally, the authors pointed out that the length of the alkyl-chain linker between the dansyl moiety and the nanoparticle surface had an influence on the fluorescence quenching efficiency, a more efficient quenching being observed when the linker was shorter, qualitatively consistent with the FRET model.46
Gu et al. studied the photophysics of UV-fluorescent fluorene-based dyes covalently attached to gold nanoparticles. Using nanosecond flash photolysis the authors showed that the triplet-triplet absorption of the fluorene moiety was suppressed in the presence of gold nanoparticles, suggesting that the rate of energy transfer from the photoexcited dye to the gold core had to be much faster than the intersystem-crossing rate of the dye.47
Huang and Murray studied the effect of gold nanoparticles on the emissive properties of a cationic dye – [Ru(bpy)3]2+; bpy = 2,2'-bipyridine.48 The phosphorescence of the dye in aqueqous solution, observed around 610 nm, was quenched after addition of gold nanoparticles with anion-rich surface ligands. This behavior suggested that the electrostatic binding of the cationic dye to the anion-rich surface of the nanoparticles resulted in energy transfer from the photoexcited [Ru(bpy)3]2+ to the nanoparticle core. Additionally, the researchers showed that the quenching of the phosphorescence was 20 times more efficient for gold nanoparticles with 2.2 nm diameter than for those with 1.8 nm diameter.48 Considering that the larger nanoparticles exhibit molar extinction coefficient larger than that for the smaller particles, the energy transfer to the particles with 2.2 nm diameter should be more efficient than that for nanoparticles with 1.8 nm diameter, in qualitative accordance to Equation 2 and the experimental findings.
Phosphorescence of [Ru(bpy)3]2+ attached to gold nanoparticles was also studied by Glomm et al.49 The authors used the time-correlated single-photon counting technique to measure excited stated lifetimes in these systems and observed more than two orders of magnitude suppression for the lifetime of the dye after attaching it to the surface of gold nanoparticles with 10 nm diameter. In this case, energy transfer as a mechanism leading to the deactivation of the excited state was argued against on the basis of the spectral properties of the studied systems and the spin-conservation principle, as the studied excited state was a triplet state.49 Instead, the authors pointed out that an electron transfer mechanism was a more likely candidate for the excited state deactivation. It should be noted, however, that the argument there was mostly speculative and the experimental techniques used by the authors did not and could not provide a direct evidence for a photoinduced electron transfer from the photoexcited [Ru(bpy)3]2+ to the gold nanoparticle.
Traditionally, Equation 2 has been used to successfully describe dipole – dipole energy transfer between molecules. However, an interaction between an organic fluorophore and a gold nanoparticle – a rather exotic species – may follow a different dependence on the relevant system parameters. One of the reports in which the authors attempted to describe the nature of the energy transfer from an organic fluorophore to a gold nanoparticle was published by Yun et al.50 In particular, the researchers addressed the question of the distance dependence between the fluorophore and the surface of a gold nanoparticle on the rate of energy transfer. A series of samples of DNA-bound fluorescein covalently attached to small, 1.4 nm in diameter, gold nanoparticles was studied in terms of the fluorescence lifetime of the organic dye. The systems were designed in such a way that the DNA strands of different length acted as rigid spacers between the nanoparticle surface and fluorescein moiety, thus allowing preparation of systems with different distance between the dye and the nanoparticle surface. The fluorescence intensities were measured for different samples and the fluorescence quenching efficiencies compared using the parameter Qeff=1-I'/I0, where I' is the fluorescence intensity of the dye attached to nanoparticles and Io is the fluorescence intensity of the dye in the absence of nanoparticles.50 Within the tested dye – nanoparticle distance range (6 nm – 23 nm) the quenching efficiency followed a :<math>\frac {1} {r_{Dye}^4-NP}\,\!</math> dependence, where :<math>\frac {1} {r_{Dye}^4-NP}\,\!</math> is the distance between the dye and the nanoparticle. This behavior is different from that expected for the FRET mechanism, from which a 1rDye-NP6 dependence would be expected. Yun et al. pointed out that the observed distance dependence of the fluorescence-quenching efficiency is in agreement with the existing description of a mechanism of energy transfer between fluorophores and metal surfaces: surface energy transfer (SET).50,51 These observations are rather surprising as the nanoparticles studied by Yun were very small and the description of the SET mechanism was developed for infinite metal surfaces.50 Subsequently, Jennings et al. reported fluorescence lifetime measurements of similar systems to those studied by Yun, including two different fluorophores – one with green fluorescence and one with red fluorescence – and demonstrated that the fluorescence quenching efficiency followed :<math>\frac {1} {r_{Dye}^4-NP}\,\!</math> dependence, consistent with the findings of Yun.52
Dulkeith et al. studied the effects of gold nanoparticles on both radiative and nonradiative rates of excited-state deactivation of lissamine dye molecules.44 The researchers examined fluorescence lifetimes and quantum yields of a series of systems incorporating lissamine molecules attached to gold nanoparticles of different sizes. It was concluded that the fluorescence quenching, i.e. the reduction of the fluorescence quantum yield, observed in the studied systems was caused not only by an efficient energy transfer from the photoexcited dye to the gold nanoparticle but also by the suppression of the radiative rate, krad, of the dye after attaching them to a gold particle. The quantum yield of fluorescence, φfl, is defined as:
- <math>\phi_{fl} = \frac {k_{rad}} {k_{rad} + k_{nr}}\,\!</math> ,Equation 3
where knr is a combined rate of all processes leading to a nonradiative deactivation of the excited state of the dye. For simple solutions of fluorescent molecules the radiative rate, krad, remains more or less unchanged, thus usually fluorescence quenching is not attributed to the changes in the natural fluorescence lifetime, τrad = 1/krad. Dulkeith et al. showed that depending on the size of the gold nanoparticles, 1 – 30 nm in diameter in their studies, the radiative rate of particle-attached lissamine molecules was decreased by as much as two orders of magnitude with respect to free dye molecules.44 At the same time the nonradiative decay rate, knr in Equation 3, increased by almost two orders of magnitude for the studied systems. Thus, according to Equation 3 the decrease in the fluorescence quantum yield was caused by both the suppression of the radiative rate and the increase of the nonradiative rate.44 Dulkeith et al. later investigated the photophysics of a red-fluorescent cyanine molecule (Cy5) attached to gold nanoparticles with a diameter of 6 nm via rigid DNA linkers.53 Again, fluorescence quenching of the dye was observed after attaching it to the surface on nanoparticles via linkers of different lengths, and the radiative rates of the dye were suppressed in all of the studied systems. In the studied range of dye-nanoparticle distances, 2 nm to 16 nm, the nonradiative rate, which was most likely dominated by energy transfer, seemed to be increased only for systems incorporating the shortest DNA linkers. For systems with the dye-nanoparticle distance larger than 4 nm the nonradiative rate seemed to be the same as that for free dye and the fluorescence quenching was governed solely by radiative rate suppression, according to Equation 3.53
The radiative rate modification by metal spheres has been described theoretically by Gersten and Nitzan.54 Using a purely classical description of an oscillating point dipole placed in close proximity of a metallic sphere with a known dielectric function, the authors calculated the effective radiative and nonradiative rate of the radiating dipole. Dipole – particle distance, particle diameter, dipole orientation with respect to the particle surface, and the dipole-oscillation frequency were found to be important parameters influencing the final values of the radiative and nonradiative rates.54
The Gersten-Nitzan (G-N) theory was used for comparison with experimental data for systems incorporating gold nanoparticles, with 10 nm and 20 nm diameters, and covalently attached dyes – [Ru(bpy)3]2+ and a substituted Pd-porphyrin (PdCS3P). Soller et al. prepared such systems and studied the effects of the gold nanoparticles on the phosphorescence of the dyes with the use of the time-correlated single-photon counting technique.55 At the distance of ca. 4 nm between the luminescent dye and the nanoparticle both [Ru(bpy)3]2+ and PdCS3P showed very similar radiative rates to those measured for free dyes in solution. The nonradiative rates of the dyes on gold nanoparticles were measured to be higher by an order of magnitude than those for the free dyes. The values of radiative and nonradiative rates calculated from the G-N theory were in very good agreement with the measured data when the authors made the assumption of a random orientation of the transition dipoles of the molecules with respect to the particle surface.55
It should be noted that the G-N theory fails to describe systems in which the distance between the luminescent dye and the nanoparticle surface is small (i.e. on the order of a nanometer). For example the experimental data of Dulkeith et al., which was previously mentioned, showed much smaller nonradiative rates than those calculated from G-N theory.44,53 Also, radiative rates calculated for a cyanine molecule (Cy5) at different distances from a gold nanoparticle surface were overestimated when compared to the measured values.53
Electron Transfer to the Nanoparticle
The possibility that electron transfer is the main channel of deactivation of excited states of organic dyes attached to gold nanoparticles has been suggested by a number of researchers and several studies addressing this hypothesis have been performed.56,57 The work of Glomm et al. regarding [Ru(bpy)3]2+ on gold nanoparticles was already mentioned.49 The expectation that gold nanoparticles may be good electron acceptors is supported by a variety of reports on their electrochemical properties. In particular it was demonstrated that gold nanoparticles can accept multiple electrons and the potential for consecutive reduction processes is dictated by the capacitance of the stabilizing alkyl ligand layer.58,59
Ipe et al. proposed that in systems involving pyrene – a UV-fluorescent dye – covalently attached to the surface of gold nanoparticles (ca. 2.5 nm in diameter) electron transfer was one of the major processes leading to the deactivation of the excited state of pyrene moiety.60 The authors used nanosecond flash photolysis in order to study the transient absorption spectra of the hybrid systems. A rather subtle change in the transient spectrum was observed when examining a solution of free pyrene and a solution of the dye attached to the surface of a nanoparticle. Based on this, the authors suggested that the change in the spectrum originated from the formation of the pyrene radical cation, which is a product in the process of photoinduced electron transfer to the gold nanoparticle.60
Barazzouk et al. found that fluorescence of chlorophyll a (Chla) is quenched in the presence of gold nanoparticles (8 nm diameter).61 Even though nanosecond transient absorption of the hybrid system showed no evidence of a radical cation of Chla, the authors favored the photoinduced electron transfer from Chla to the gold nanoparticle as the main deactivation channel of the excited state of the dye. The following experiment, showing results consistent with photoinduced electron transfer, was performed and used to support the interpretation. The authors prepared an indium tin oxide electrode coated with gold nanoparticles onto which Chla molecules were deposited. The authors showed that upon applying a negative potential to the electrode the quenching of the emission of Chla by gold nanoparticles was reduced. It was concluded that this behavior was consistent with the suppression of the photoinduced electron transfer by negatively charging of the gold nanoparticles.61
van Herrikhuyzen et al. used a femtosecond transient absorption setup to study the effect of gold nanoparticles (ca. 1.6 nm and 4.1 nm in diameter) on the photophysics of oligo(phenylene-vinylene) (OPV) covalently attached to the nanoparticle surface.62 Even though the signal from the metallic core of the particles dominated the measured transient absorption traces the authors, were able to conclude that the measured traces were consistent with ultrafast energy transfer, which limited the lifetime of the organic dye to 2 ps. The authors demonstrated no measurable electron transfer taking place in the studied system, thus limiting the number of processes of the excited-state deactivation of the organic dye to the energy transfer.62
Intermolecular Interactions
As shown in Figure 4 intermolecular interactions may play a role in the deactivation of excited state of dyes attached to gold nanoparticles.45 The high local density of dyes packed on the metal surface can in principle facilitate such interactions.
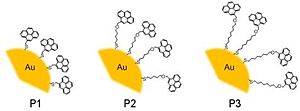
Ipe and Thomas prepared a series of gold nanoparticles coated with pyrene-based ligands with alkyl spacers of different chain length as shown in Figure 5.63
Fluorescence spectra of toluene solutions of P2 and P3 showed a feature characteristic of the excimer emission of the pyrene moiety. Additionally systems similar to P2 and P3 in which pyrene-thiols were used in mixtures with dodecanethiol as the stabilizing ligands of gold nanoparticles showed a decreased signal from pyrene excimers. This was interpreted as being consistent with the formation of pyrene excimers on the surface of nanoparticles, by invoking the dilution of pyrene moieties on the surface in the pyrene-thiol / dodecanethiol systems. The authors further argued that the structural ability of the pyrene moieties in P2 and P3 to align themselves after the photoexcitation to the geometry that allows for excimer formation makes this process efficient on the surface of gold nanoparticles. On the other hand, the researchers concluded, due to a relatively more rigid linker between the anchoring sulfur atom and the pyrene moiety than in P2 and P2, P1 showed no excimer formation.63 Interestingly, fluorescence decay data showed that the pyrene-fluorescence lifetimes in the studied nanoparticle systems were not changed appreciably when compared to the fluorescence decay of the corresponding free pyrene-thiol dyes in toluene solution. Based on that observation the authors ruled out a possibility of pyrene-excited-state quenching due to energy or electron transfer.63
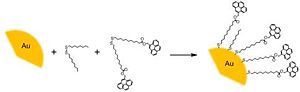
It is interesting to compare the data of Ipe and Thomas to another report on fluorescence studies of pyrene-thiol coated gold nanoparticles. Werts et al. showed that adsorption of a disulfide bearing two pyrene moieties, showing efficient intramolecular excimer formation, onto the surface of gold nanoparticles (the representation of the reaction is shown in Figure 6) causes a decrease of the excimer emission relative to the monomer emission of pyrene.64 This implies that the pyrene-excimer formation on the surface of gold nanoparticles is less efficient than its formation in the case of the pyrene moieties bound in the form of a disulfide.
The starting gold nanoparticles were stabilized with tetraoctylammonium bromide (TOAB) which is not shown in the scheme. Such nanoparticles are referred to as “naked nanoparticles” as TOAB is readily displaced by thiol ligands.
Combining the data of Werts et al. and the findings of Ipe and Thomas, especially the unchanged fluorescence lifetime of the hybrid systems in Ipe’s work, suggests it is possible that Ipe and Thomas probed the fluorescence emission of pyrene disulfides, which do show pyrene-excimer emission, as demonstrated by Werts.63,64 This of course poses the question of the origin of pyrene disulfides in P2 and P3 studied by Ipe and Thomas. Actually, the first step of the preparation of gold nanoparticles followed by Ipe, the so-called Brust synthesis,16 involves reduction of a Au(III) salt to a Au(I) compound with a portion of the thiols used in the synthesis being oxidized to disulfides.65 Perhaps after the synthesis of the nanoparticles small amounts of pyrene-disulfide impurities were still present in the samples that Ipe and Thomas studied and the observed fluorescence was dominated by the signal from these disulfides. This would be possible only if the fluorescence from particle-bound pyrene moieties was greatly quenched. The fluorescence quantum yield contrast between the surface-bound pyrene and pyrene disulfide would result in the latter dominating the fluorescence signal. This may well be the case as Ipe and Thomas mentioned the existence of a small fraction of fluorescence signal with greatly reduced fluorescence lifetime in the studied hybrid systems.
This alternative interpretation of the published data is of course only speculative, but it opens a question about the usefulness of fluorescence-based techniques in the studies of the excited-state deactivation of organic dyes attached to gold nanoparticles. The presence of small amounts of highly fluorescent impurities in samples which possibly have minimal fluorescence quantum yields, because the fluorescence of dyes is quenched by gold nanoparticles, can in principle lead to the measured signal being dominated by emission from the impurities rather than by emission from the systems of interest.
References
(1)Ruivo, A.; Gomes, C.; Lima, A.; Botelho, M. L.; Melo, R.; Belchior, A.; Pires de Matos, A. J. Cult. Herit. 2008, 9, e134-e137.
(2)Wagner, F. E.; Haslbeck, S.; Stievano, L.; Calogero, S.; Pankhurst, Q. A.; Martinek, P. Nature 2000, 407, 691-692.
(3)Daniel, M. C.; Astruc, D. Chemical Reviews (Washington, DC, United States) 2004, 104, 293-346.
(4)Carbert, J. Gold Bull. 1980, 13, 144-50.
(5)Hunt, L. Gold Bull. 1976, 9, 134-39.
(6)Ware, M. Gold Bull 2006, 39, 124-131.
(7)Faraday, M. Philos. Trans. R. Soc. London 1857, 147, 145-181.
(8)Link, S.; El-Sayed, M. A. Annu. Rev. Phys. Chem. 2003, 54, 331-366.
(9)Zsigmondy, R. Liebigs Ann. 1898, 301, 361-87.
(11)Garnett, J. C. M. Philos. Trans. R. Soc. London, Ser. A 1904, 203, 385-420.
(12)Garnett, J. C. M. Philos. Trans. R. Soc. London, Ser. A 1906, 205, 237-288.
(13)Mie, G. Ann. Physik 1908, 25, 377-445.
(14)Underwood, S.; Mulvaney, P. Langmuir 1994, 10, 3427-30.
(15)Mulvaney, P. Langmuir 1996, 12, 788-800.
(16)Brust, M.; Walker, M.; Bethell, D.; Schiffrin, D. J.; Whyman, R. J. Chem. Soc., Chem. Commun. 1994, 801-2.
(17)Suppan, P. Chemistry and Light; The Royal Society of Chemistry: Cambridge, 1994.
(18)Hodak, J. H.; Henglein, A.; Hartland, G. V. J. Phys. Chem. B 2000, 104, 9954-9965.
(19)Kelly, K. L.; Coronado, E.; Zhao, L. L.; Schatz, G. C. J. Phys. Chem. B 2003, 107, 668-677.
(20)Berlman, I. B. Handbook of fluorescence spectra of aromatic compounds; 2nd ed.; Academic Press: New York, 1971.
(21)Liu, X.; Atwater, M.; Wang, J.; Huo, Q. Colloids and Surfaces B: Biointerfaces 2007, 58, 3-7.
(22)Link, S.; El-Sayed, M. A. J. Phys. Chem. B 1999, 103, 8410-8426.
(23)Alvarez, M. M.; Khoury, J. T.; Schaaff, T. G.; Shafigullin, M. N.; Vezmar, I.; Whetten, R. L. J. Phys. Chem. B 1997, 101, 3706-3712.
(24)Dulkeith, E.; Niedereichholz, T.; Klar, T. A.; Feldmann, J.; von Plessen, G.; Gittins, D. I.; Mayya, K. S.; Caruso, F. Physical Review B 2004, 70, 205424.
(25)Logunov, S. L.; Ahmadi, T. S.; El-Sayed, M. A.; Khoury, J. T.; Whetten, R. L. J. Phys. Chem. B 1997, 101, 3713-3719.
(26)Sun, C. K.; Vallée, F.; Acioli, L. H.; Ippen, E. P.; Fujimoto, J. G. Physical Review B 1994, 50, 15337.
(27)Hodak, J. H.; Martini, I.; Hartland, G. V. The Journal of Chemical Physics 1998, 108, 9210-9213.
(28)Hu, M.; Hartland, G. V. J. Phys. Chem. B 2002, 106, 7029-7033.
(29)Zijlstra, P.; Chon, J. W. M.; Gu, M. Nature 2009, 459, 410-413.
(30)Huang, X.; Jain, P. K.; El-Sayed, I. H.; El-Sayed, M. A. Nanomedicine 2007, 2, 681-693.
(31)Hao, E.; Schatz, G. C. J. Chem. Phys. 2004, 120, 357-366.
(32)Zeman, E. J.; Schatz, G. C. J. Phys. Chem. 1987, 91, 634-643.
(33)Chen, C. J.; Osgood, R. M. Applied Physics A Solids and Surfaces 1983, A31, 171-82.
(34)Chen, C. K.; de Castro, A. R. B.; Shen, Y. R. Phys. Rev. Lett. 1981, 46, 145.
(35)Boyd, G. T.; Rasing, T.; Leite, J. R. R.; Shen, Y. R. Physical Review B 1984, 30, 519.
(36)Jeanmaire, D. L.; Van Duyne, R. P. J. Electroanal. Chem. 1977, 84, 1-20.
(37)Kneipp, K.; Kneipp, H.; Itzkan, I.; Dasari, R. R.; Feld, M. S. Chem. Rev. (Washington, D. C.) 1999, 99, 2957-2975.
(38)Kudelski, A. Surf. Sci. 2009, 603, 1328-1334.
(39)Wenseleers, W.; Stellacci, F.; Meyer-Friedrichsen, T.; Mangel, T.; Bauer, C. A.; Pond, S. J. K.; Marder, S. R.; Perry, J. W. J. Phys. Chem. B 2002, 106, 6853-6863.
(40)Cohanoschi, I.; Hernandez, F. E. J. Phys. Chem. B 2005, 109, 14506-14512.
(41)Huang, C.-C.; Chang, H.-T. Anal. Chem. 2006, 78, 8332-8338.
(42)Griffin, J.; Singh, A. K.; Senapati, D.; Rhodes, P.; Mitchell, K.; Robsinson, B.; Yu, E.; Ray, P. C. Chemistry--A European Journal 2009, 15, 342-351.
(43)Shang, L.; Qin, C.; Wang, T.; Wang, M.; Wang, L.; Dong, S. J. Phys. Chem. C 2007, 111, 13414-13417.
(44)Dulkeith, E.; Morteani, A. C.; Niedereichholz, T.; Klar, T. A.; Feldmann, J.; Levi, S. A.; van Veggel, F. C. J. M.; Reinhoudt, D. N.; Moller, M.; Gittins, D. I. Phys. Rev. Lett. 2002, 89, 203002/1-203002/4.
(45)Thomas, K. G.; Kamat, P. V. Acc. Chem. Res. 2003, 36, 888-898.
(46)Aguila, A.; Murray, R. W. Langmuir 2000, 16, 5949-5954.
(47)Gu, T.; Whitesell, J. K.; Fox, M. A. Chem. Mater. 2003, 15, 1358-1366.
(48)Huang, T.; Murray, R. W. Langmuir 2002, 18, 7077-7081.
(49)Glomm, W. R.; Moses, S. J.; Brennaman, M. K.; Papanikolas, J. M.; Franzen, S. The Journal of Physical Chemistry B 2004, 109, 804-810.
(50)Yun, C. S.; Javier, A.; Jennings, T.; Fisher, M.; Hira, S.; Peterson, S.; Hopkins, B.; Reich, N. O.; Strouse, G. F. J. Am. Chem. Soc. 2005, 127, 3115-3119.
(51)Persson, B. N. J.; Lang, N. D. Physical Review B 1982, 26, 5409.
(52)Jennings, T. L.; Singh, M. P.; Strouse, G. F. J. Am. Chem. Soc. 2006, 128, 5462-5467.
(53)Dulkeith, E.; Ringler, M.; Klar, T. A.; Feldmann, J.; Munoz Javier, A.; Parak, W. J. Nano Lett 2005, 5, 585-589.
(54)Gersten, J.; Nitzan, A. J. Chem. Phys. 1981, 75, 1139-52.
(55)Soller, T.; Ringler, M.; Wunderlich, M.; Klar, T. A.; Feldmann, J.; Josel, H. P.; Markert, Y.; Nichtl, A.; Kuerzinger, K. Nano Lett. 2007, 7, 1941-1946.
(56)Kotiaho, A.; Lahtinen, R.; Lehtivuori, H.; Tkachenko, N. V.; Lemmetyinen, H. Journal of Physical Chemistry C 2008, 112, 10316-10322.
(57)Kotiaho, A.; Lahtinen, R. M.; Tkachenko, N. V.; Efirnov, A.; Kira, A.; Imahori, H.; Lemmetyinen, H. Langmuir 2007, 23, 13117-13125.
(58)Hicks, J. F.; Templeton, A. C.; Chen, S.; Sheran, K. M.; Jasti, R.; Murray, R. W.; Debord, J.; Schaaff, T. G.; Whetten, R. L. Anal. Chem. 1999, 71, 3703-3711.
(59)Hicks, J. F.; Miles, D. T.; Murray, R. W. J. Am. Chem. Soc. 2002, 124, 13322-13328.
(60)Ipe, B. I.; Thomas, K. G.; Barazzouk, S.; Hotchandani, S.; Kamat, P. V. J. Phys. Chem. B 2002, 106, 18-21.
(61)Barazzouk, S.; Kamat, P. V.; Hotchandani, S. J. Phys. Chem. B 2005, 109, 716-723.
(62)van Herrikhuyzen, J.; Janssen, R. A. J.; Schenning, A. P. H. J.; Meskers, S. C. J. Chem. Phys. Lett. 2007, 433, 340-344.
(63)Ipe, B. I.; Thomas, K. G. J. Phys. Chem. B 2004, 108, 13265-13272.
(64)Werts, M. H. V.; Zaim, H.; Blanchard-Desce, M. Photochem. Photobiol. Sci. 2004, 3, 29-32.
(65)Chen, S.; Templeton, A. C.; Murray, R. W. Langmuir 2000, 16, 3543-3548.
References
- ↑ Daniel, M. C.; Astruc, D. Chemical Reviews (Washington, DC, United States) 2004, 104, 293-346.
- ↑ Ruivo, A.; Gomes, C.; Lima, A.; Botelho, M. L.; Melo, R.; Belchior, A.; Pires de Matos, A. J. Cult. Herit. 2008, 9, e134-e137.
- ↑ Wagner, F. E.; Haslbeck, S.; Stievano, L.; Calogero, S.; Pankhurst, Q. A.; Martinek, P. Nature 2000, 407, 691-692 1,2
- ↑ Carbert, J. Gold Bull. 1980, 13, 144-50.
- ↑ Hunt, L. Gold Bull. 1976, 9, 134-39
- ↑ Ware, M. Gold Bull 2006, 39, 124-131.
- ↑ Ware, M. Gold Bull 2006, 39, 124-131.
- ↑ Link, S.; El-Sayed, M. A. Annu. Rev. Phys. Chem. 2003, 54, 331-366.
- ↑ Logunov, S. L.; Ahmadi, T. S.; El-Sayed, M. A.; Khoury, J. T.; Whetten, R. L. J. Phys. Chem. B 1997, 101, 3713-3719.