Electromagnetic Radiation
| Previous Topic | Return to Basics of Light Menu | Next Topic |
It helpful to become familiar with the geography of the electromagnetic spectrum. Try to memorize some common wavelengths, frequencies, energies and associated timescales.
The Nature of Light
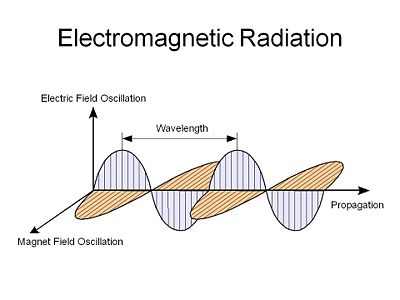
Light is an electromagnetic radiation, an electric field that oscillates in both time and space along with a corresponding orthogonal magnetic field that oscillates with the same spatial and temporal periodicity. This was first described by Maxwell.
When light gets into a material it interacts with the charged particles within the atoms. Although both magnetic and electric field can be absorbed by materials, the interaction of the field of light is usually about 105 stronger than that of the magnetic field and thus to the first approximation we can concern ourselves only with the interaction of the electric field with matter. When the electric field of light gets into a material and it cause the electrons to move.
Formally, the term “light” is strictly applicable to the visible portion of the electromagnetic spectrum, however we will use a looser definition that includes the entire visible and non-visible spectrum.
Light behaves both as wave with properties of wavelength and frequency and as particle in that it is quantized in discrete packets known as photons.
- <math>c=\lambda \nu\,\!</math>
where:
- <math>\lambda\,\!</math> is wavelength is measured in nanometers (nm)
- <math>\nu\,\!</math>is frequency (1/T Period T in seconds) measured in Hertz
Light as a wave
The light waves can be described as:
- <math>F = F_o sin [(2\pi/ \lambda) (x-vt) + \phi]\,\!</math>
- <math>=F_o sin [k(x-\lambda vt) + \phi]\,\!</math>
- <math>=F_o sin [kx- \omega t + \phi]\,\!</math>
where;
- <math>K \equiv \frac{2\pi} {\lambda}\,\!</math> = wave vector or wavenumber in cm-1
- x is direction of travel
- <math>F_o\,\!</math> is the amplitude
- <math>\omega = 2\pi \nu\,\!</math> = angular frequency ( in radians/s)
- <math>\phi\,\!</math> is the phase constant that accounts for a non-zero amplitude at the origin of the plot.
Light as a Particle
The energy of the light beam is embodied in as particles called photons.
- <math>E = \frac{h}{\nu}\,\!</math>
- <math>h\,\!</math> is plancks constant = 6.6 x 10-34 J·S in SI units
Which can be divided by the charge of the electron 1.6 x 10-19 coulomb to give a microscopic equivalent of
E= 4.14 x 10-15 eV·s
The speed of light in a vacuum at approximately 3 x 108 m/s
The Electromagnetic Spectrum

In the ultraviolet photons have 3 to 30 eV energies, in the range of 100 to 1000 eV there are soft x-rays, and beyond that hard x-rays. The visible spectrum has wavelengths of a nanometer. But in the soft x-rays wavelengths are in the order of angstroms. This is why you can use the diffraction of soft x-rays to explore the crystal structure of molecules; the wavelength is in the approximate scale of that of atoms and bonds. Gamma rays are in the range of mega eV.
On the lower energy end of the electronmagnetic spectrum there is the infrared. The IR spectrum of a π conjugated system reveals the bond stretching of a CC double bond at about 1600 wave numbers or about .2 eV and the frequency in the sub picosecond regime. A π conjugated molecule in an excited state undergoes bond length relaxation in few tenths of a picosecond. Motion of molecules as a whole involve 20-50 wave numbers in the millivolt scale, and timescales of 10-100 pico seconds.
Beyond that the microwave and radio wave have wavelengths that are very large, in the mega or kilohertz. It is useful to keep in mind the relations between the wavelengths, spectrum and energies.
- 1 eV = 1.6 x10-19 J
- = 96.5 kJ/mol ~100 kJ/mol
- ~23kcal/mol
- = 8065 cm-1 (wave numbers)
Try your hand at The EM Quiz
Explore the Wavelength Calculator Applet
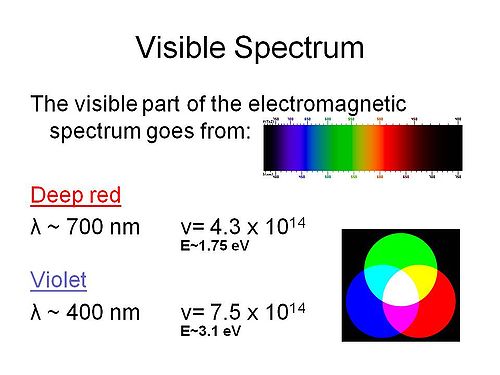
Visible spectrum
The energies of the spectrum vary from about 3eV on the violet side to 1.5eV on the red side in approximate terms. The frequencies are in the mid 1014 scales. This is important because it determines the time scales for events. For example an event such as energy transition in a π conjugated system which will be 2 or 3eV, this is in the range of the visible spectra frequencies so the timescale for that process will be in the femptoseconds.
The colors red, green, and blue (RGB) colors combine to create white light (additive colors). You can also combine magenta and green to create white light.
Converting from wavelength to eV
It is possible to quickly convert from wavelength to electron volts (E) using:
- <math>E = h\nu = \frac{hc}{\lambda}\,\!</math>
where:
- <math>h\,\!</math> is Planck's constant
- <math>c\,\!</math> is the speed of light.
- <math>\nu\,\!</math> is frequency
- <math>\lambda\,\!</math> is wavelength
for convenience:
- <math>hc = \left (4.13566833\times10^{-19}eV\cdot s \right )\left( 2.998\times10^{8}\frac{m}{s} \right ) \approx 1240 eV \cdot nm\;\!</math>
or ν ≅ 2.5×1014Hz and λ ≅ 1240nm to give
- <math>E(eV) \approx \frac{1240 eV \cdot nm}{\lambda (nm)}\,\!</math>
Simple divide the wavelength in nanometers into 1240 to calculate the eVs.
So a light beam at 600 nm you take 1240/600 that is about 2 eV and it is in the yellow portion of the spectrum. Or 400 nm gives 3eV and so on.
Thermal Energy
- kT (300K) is the thermal energy at 300K
- ~0.025 eV
- ~2.5 kJ/mol
- ~0.6 kcal/mol
- ~200 cm-1 (wave numbers)
Thus a crystal of π- conjugated material at room temperature requires 1600 wave numbers for CC bond stretching, there is not enough energy at room temperature to excite it. On the other hand motions of the whole molecule that only require 50 wave numbers can achieve this level of excitation at room temperature. These estimations help you determine if you have the right amount of energy and an appropriate timescale for the process that you are working with.
Uncertainty and precision
We have now developed lasers with pulses less than a femtosecond. But if you have a pulse that is on the order of one femtosecond, the precision on the energy can be as large as few eV. The faster the pulse, the less the precision of energy. If you are trying to study energy very accurately you don’t want to use the fastest pulses because it hurts the accuracy of your energy measurement. Its better to stay with picosecond laser pulses for this. If, on the other hand, you are trying follow chemical reactions in real time, then you need to go with faster and faster lasers at the expense of energy information precision. This is all a result of Heisenberg's uncertainty principle.
The precision of the energy times the precision of the time has to be large, i.e. > h/4π
- <math>\Delta E \cdot \Delta t > \frac{h}{4\pi}\,\!</math>
- <math>h = 4.14 \times 10^{-15} eV\cdot s\,\!</math>
- <math>\frac{h}{4\pi}= 3.3 \times 10^{-16} eV\cdot s\,\!</math>
For light:
- <math>E = hv = h/t\,\!</math>
- <math>E \cdot t = h(>\frac{h}{4\pi})\,\!</math>
- For t = 5 x 10-15 s : E~0.8eV
A vibration at 1600 cm-1 (~0.2eV) will be seen in the time domain as an oscillation with a period of ~20 fs.
Please note that others may also have edited the contents of this article.
|
| Previous Topic | Return to Basics of Light Menu | Next Topic |