Difference between revisions of "Jablonksi Diagram"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) m (→External Links) |
||
| (28 intermediate revisions by 2 users not shown) | |||
| Line 7: | Line 7: | ||
</table> | </table> | ||
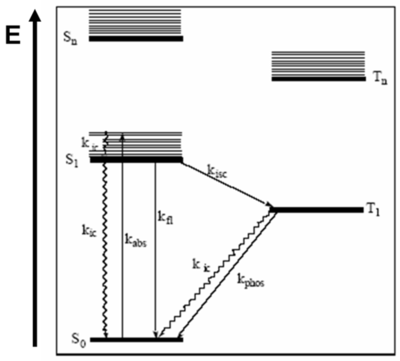
Jablonski diagrams are common representations of the possible electronic states and transitions as molecules enter and leave the excited state. Aleksander Jabłoński was a Polish scientist who did significant research on fluorescence and molecular photophysics in the 1930's. Jablonski diagrams describe the electronic states of molecules, transitions and associated light emitting phenomena. Though Jablonski diagrams resemble one-electron bandgap diagrams, they represent different things. Horizontal lines in a Jablonski diagram represent energetic states of a molecule or system, not the discrete electronic energy levels depicted in one-electron diagrams. | |||
[[Image:Jablonski.png|thumb|400px|Several processes are illustrated and are indicated by the rate constants that characterize the processes shown, including absorption of light, fluorescence, internal conversion, intersystem crossing and phosphorescence]] | [[Image:Jablonski.png|thumb|400px|Several processes are illustrated and are indicated by the rate constants that characterize the processes shown, including absorption of light, fluorescence, internal conversion, intersystem crossing and phosphorescence]] | ||
| Line 12: | Line 13: | ||
=== Meaning of Levels === | === Meaning of Levels === | ||
It is important to understand the premises of the Jablonski Diagrams. | It is important to understand the premises of the Jablonski Diagrams. | ||
:'''S<sub>0</sub>''' is the ground state of the molecule, | :'''S<sub>0</sub>''' is the ground state of the molecule, | ||
:'''S<sub>1</sub>''' is the first excited state and S<sub>n</sub> is the nth excited state. | :'''S<sub>1</sub>''' is the first excited singlet state and S<sub>n</sub> is the nth excited state. | ||
:'''T<sub>1</sub>''' is the first excited triplet state and T<sub>n</sub> is the nth excited state. | |||
The y-axis, labeled E, indicates the relative energies of the states. In more complex Jablonski diagrams, the states can be also described as potential energy surfaces. Within each electronic state exist a range of vibrational levels. Vibrational ground states are shown with thick lines and higher vibrational states are shown with thin lines. | |||
Molecules can progress from state to state via either radiative or nonradiative processes. Graphically, nonradiative transitions are shown as straight lines and radiative transitions are shown with squiggly lines on a Jablonski diagram. | |||
The spin multiplicity of states are spatially separated along the x-axis of a Jablonski diagram. Singlet spin multiplicity exists when the total spin of the system is zero. Since any plus ½ spin corresponds to a minus ½ spin, the total spin results as zero. There is a single way of putting all the spins so this is referred to as a '''singlet state'''. It is also possible to have '''triplet states''' that have total spin number is +1. | |||
:'''T<sub>1</sub>''' shows the lowest excited triplet state. S<sub>1</sub> refers to the excited singlet state. The 0 refers to the ground state. | :'''T<sub>1</sub>''' shows the lowest excited triplet state. S<sub>1</sub> refers to the excited singlet state. The 0 refers to the ground state. | ||
:'''T<sub>n</sub>''' is also a higher lying triplet state | :'''T<sub>n</sub>''' is also a higher lying triplet state | ||
Usually, when drawing or writing a Jablonski Diagram, the singlet states are on the left hand side. In the case of singlet states, the total spin number is zero and the molecule is [[diamagnetic]]. In most instances, those π-conjugated molecules in the ground state have spins that are all paired. Molecules with triplet states are drawn on the right hand side and the molecules are [[paramagnetic]]. An example of a paramagnetic molecule is oxygen, that has two π levels that have the same energy and therefore, the two electrons point upwards. What is referred to as singlet oxygen is actually 1 eV above the ground state of oxygen and it is a pretty nasty molecule. | |||
=== Excitation === | === Excitation === | ||
In general, chromophores have a ground state that is a singlet and an excited state that will be singlet or sometimes triplets. Light emitting systems deal with triplet states. That is why triplets are important. Once the molecules are excited, many photophysical processes can occur. When the molecule that is in the ground state is excited, the photon energy will bring it into the S<sub>1</sub> electronic state at a higher vibrational level. Once we have the absorption '''K<sub>abs</sub>''', the molecule can trickle back down from the maximum line in the S<sub>1</sub> to the minimum of the S<sub>1</sub> state. It does that by going down the vibrational levels and therefore, vibrations are created in the molecule. That is how the molecule loses its energy. This process is referred to as internal conversion ('''k<sub>ic</sub>''') because it remains within the same spin manifold and possibly within the same excited states. Then from the minimum of S<sub>1</sub>, the molecule can also decay back to the ground state without the emission of a photon (non-radiativeally). This is not a good thing when we are interested in light emission. It could also decay back to the ground state by emitting a photon, which is referred to as a fluorescence phenomenon ('''k<sub>fl</sub>'''). All these processes have rates that are generally typical for conjugated molecules. | In general, chromophores have a ground state that is a singlet and an excited state that will be singlet or sometimes triplets. Light emitting systems deal with triplet states. That is why triplets are important. Once the molecules are excited, many photophysical processes can occur. When the molecule that is in the ground state is excited, the photon energy will bring it into the S<sub>1</sub> electronic state at a higher vibrational level. Once we have the absorption '''K<sub>abs</sub>''', the molecule can trickle back down from the maximum line in the S<sub>1</sub> to the minimum of the S<sub>1</sub> state. It does that by going down the vibrational levels and therefore, vibrations are created in the molecule. That is how the molecule loses its energy. This process is referred to as '''internal conversion''' ('''k<sub>ic</sub>''') because it remains within the same spin manifold and possibly within the same excited states. Then from the minimum of S<sub>1</sub>, the molecule can also decay back to the ground state without the emission of a photon (non-radiativeally). This is not a good thing when we are interested in light emission. It could also decay back to the ground state by emitting a photon, which is referred to as a '''fluorescence''' phenomenon ('''k<sub>fl</sub>'''). All these processes have rates that are generally typical for conjugated molecules. | ||
Starting at S<sub>0</sub> a photon is absorbed, spin multiplicity is conserved, and the electron gets into S<sub>1</sub>. Then in some instances, a crossover to the triplet manifold T<sub>1</sub> can occur. This crossover to the triplet manifold is referred to as intersystem crossing. The '''K<sub>isc</sub>''' shown between S<sub>1</sub> and T<sub>1</sub> represents the intersystem crossing. The intersystem crossing can cause molecule to trickle down back to the bottom of T<sub>1</sub>, thus intersystem crossing is followed by internal conversion. At the bottom of the T<sub>1</sub> state, the molecule usually lives for a pretty long time. Since it is metastable, the probability of it descending back to the ground state is small but even so eventually happens. If it occurs radiadivally then a phosphorescence can be produced. It could also come down from T<sub>1</sub> via emission of vibrations through internal conversion. Molecules that are efficient enough to be used in a display must have very large rates for fluorescence or phosphorescence. With a molecule such as naphtaline, a flat hypercarbon, the probability of this fluoresence occuring is extremely small. But there is a way to increase the probability. | Starting at S<sub>0</sub> a photon is absorbed, spin multiplicity is conserved, and the electron gets into S<sub>1</sub>. Then in some instances, a crossover to the triplet manifold T<sub>1</sub> can occur. This crossover to the triplet manifold is referred to as intersystem crossing. The '''K<sub>isc</sub>''' shown between S<sub>1</sub> and T<sub>1</sub> represents the intersystem crossing. The intersystem crossing can cause molecule to trickle down back to the bottom of T<sub>1</sub>, thus intersystem crossing is followed by internal conversion. At the bottom of the T<sub>1</sub> state, the molecule usually lives for a pretty long time. Since it is metastable, the probability of it descending back to the ground state is small but even so eventually happens. If it occurs radiadivally then a phosphorescence can be produced. It could also come down from T<sub>1</sub> via emission of vibrations through internal conversion. Molecules that are efficient enough to be used in a display must have very large rates for fluorescence or phosphorescence. With a molecule such as naphtaline, a flat hypercarbon, the probability of this fluoresence occuring is extremely small. But there is a way to increase the probability. | ||
| Line 33: | Line 42: | ||
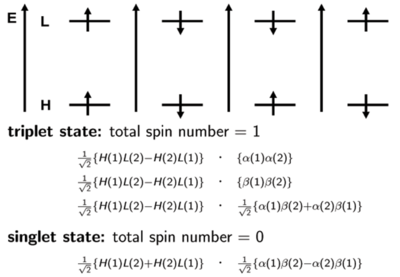
[[Image:Singlettripletspin.png|thumb|400px|This slide shows you the distinction between a singlet and triplet.]] | [[Image:Singlettripletspin.png|thumb|400px|This slide shows you the distinction between a singlet and triplet.]] | ||
It is important to know that states refer to the multi-electron system. We will make an approximation and simply look at the orbital levels, HOMO, LUMO and so on. In a large number of cases, the first excited state can mainly be described by the promotion of an electron from the HOMO level to the LUMO Level. The first energy level diagram of the four shows a spin of +1/2 in the HOMO and a spin of +1/2 in the LUMO. (This doesn’t mean that this first case always occurs in excitation; it is just possible to have this situation at some point.) In this case, the two spins are aligned and the total spin number is 1. This case is one of the triplet states. Another triplet state can occur like the 2nd energy diagram shown on the right of the first. It is also possible to have opposite spins. The third diagram shows a situation where the spin is +½ or what I refer to as alpha on the HOMO, and the spin is -½ or beta on the LUMO. The fourth diagram shows the reverse of the third: there is a -1/2 beta on the HOMO and +1/2 alpha on the LUMO. The first two situations and diagrams represent pure quanta-mechanical spin states. However, the last two are not; only their combination is. Therefore, there are two ways to obtain a triplet state. One way to have both electron spins to have the same direction. The way is to take the linear positive combination of the last two diagrams. This is done on the slide with the proper normalization factor; the alpha for electron 1 and beta for electron 2 plus the fourth diagram which has an alpha for electron 2 and beta for electron 1. This defines the third triplet configuration. | It is important to know that states refer to the multi-electron system. We will make an approximation and simply look at the orbital levels, HOMO, LUMO and so on. In a large number of cases, the first excited state can mainly be described by the promotion of an electron from the HOMO level to the LUMO Level. The first energy level diagram of the four shows a spin of +1/2 in the HOMO and a spin of +1/2 in the LUMO. (This doesn’t mean that this first case always occurs in excitation; it is just possible to have this situation at some point.) In this case, the two spins are aligned and the total spin number is 1. This case is one of the triplet states. Another triplet state can occur like the 2nd energy diagram shown on the right of the first. It is also possible to have opposite spins. The third diagram shows a situation where the spin is +½ or what I refer to as α on the HOMO, and the spin is -½ or β on the LUMO. The fourth diagram shows the reverse of the third: there is a -1/2 β on the HOMO and +1/2 α on the LUMO. The first two situations and diagrams represent pure quanta-mechanical spin states. However, the last two are not; only their combination is. Therefore, there are two ways to obtain a triplet state. One way to have both electron spins to have the same direction. The way is to take the linear positive combination of the last two diagrams. This is done on the slide with the proper normalization factor; the α for electron 1 and β for electron 2 plus the fourth diagram which has an α for electron 2 and β for electron 1. This defines the third triplet configuration. | ||
<br clear='all'> | |||
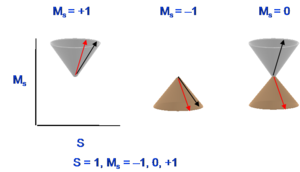
[[Image:Spinstates.png|thumb|300px|Magnetic numbers for triplet state]] | |||
Thus, the triplet state has a multiplicity of three with magnetic numbers of +1 (first diagram), -1(second diagram), and 0(combination of the last two diagrams), and total spin number in all cases is equal to 1. The singlet state is the subtraction of those two spin configurations in the last two diagrams. Usually, when referring to a singlet state, there is one spin like with an upward direction and the other spin has a downward direction. However, the quantum mechanical situation is a bit more complex than what this leads you to believe. For the triplet, the two spin configurations are easy to pinpoint but the third one only exists in combination. Remember that the third spin configuration diagram and the last spin configuration do not correspond to pure states. Their plus and minus combination is necessary to get to the actual spin state. | Thus, the triplet state has a multiplicity of three with magnetic numbers of +1 (first diagram), -1(second diagram), and 0(combination of the last two diagrams), and total spin number in all cases is equal to 1. The singlet state is the subtraction of those two spin configurations in the last two diagrams. Usually, when referring to a singlet state, there is one spin like with an upward direction and the other spin has a downward direction. However, the quantum mechanical situation is a bit more complex than what this leads you to believe. For the triplet, the two spin configurations are easy to pinpoint but the third one only exists in combination. Remember that the third spin configuration diagram and the last spin configuration do not correspond to pure states. Their plus and minus combination is necessary to get to the actual spin state. | ||
== External Links == | |||
* [http://micro.magnet.fsu.edu/primer/java/jablonski/lightandcolor/index.html Florida State University: Jablonski diagram primer] | |||
[http:// | *[[wikipedia:Jablonski_diagram]] | ||
*[http://www.shsu.edu/~chm_tgc/sounds/flashfiles/Jablonski.scrubber.swf Flash animation of processes involved in Jablonski diagram- Sam Houston University] | |||
[[category:absorption]] | |||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
Latest revision as of 11:04, 10 August 2010
| Previous Topic | Return to Absorption and Emission Menu | Next Topic |
Jablonski diagrams are common representations of the possible electronic states and transitions as molecules enter and leave the excited state. Aleksander Jabłoński was a Polish scientist who did significant research on fluorescence and molecular photophysics in the 1930's. Jablonski diagrams describe the electronic states of molecules, transitions and associated light emitting phenomena. Though Jablonski diagrams resemble one-electron bandgap diagrams, they represent different things. Horizontal lines in a Jablonski diagram represent energetic states of a molecule or system, not the discrete electronic energy levels depicted in one-electron diagrams.
Meaning of Levels
It is important to understand the premises of the Jablonski Diagrams.
- S0 is the ground state of the molecule,
- S1 is the first excited singlet state and Sn is the nth excited state.
- T1 is the first excited triplet state and Tn is the nth excited state.
The y-axis, labeled E, indicates the relative energies of the states. In more complex Jablonski diagrams, the states can be also described as potential energy surfaces. Within each electronic state exist a range of vibrational levels. Vibrational ground states are shown with thick lines and higher vibrational states are shown with thin lines.
Molecules can progress from state to state via either radiative or nonradiative processes. Graphically, nonradiative transitions are shown as straight lines and radiative transitions are shown with squiggly lines on a Jablonski diagram.
The spin multiplicity of states are spatially separated along the x-axis of a Jablonski diagram. Singlet spin multiplicity exists when the total spin of the system is zero. Since any plus ½ spin corresponds to a minus ½ spin, the total spin results as zero. There is a single way of putting all the spins so this is referred to as a singlet state. It is also possible to have triplet states that have total spin number is +1.
- T1 shows the lowest excited triplet state. S1 refers to the excited singlet state. The 0 refers to the ground state.
- Tn is also a higher lying triplet state
Usually, when drawing or writing a Jablonski Diagram, the singlet states are on the left hand side. In the case of singlet states, the total spin number is zero and the molecule is diamagnetic. In most instances, those π-conjugated molecules in the ground state have spins that are all paired. Molecules with triplet states are drawn on the right hand side and the molecules are paramagnetic. An example of a paramagnetic molecule is oxygen, that has two π levels that have the same energy and therefore, the two electrons point upwards. What is referred to as singlet oxygen is actually 1 eV above the ground state of oxygen and it is a pretty nasty molecule.
Excitation
In general, chromophores have a ground state that is a singlet and an excited state that will be singlet or sometimes triplets. Light emitting systems deal with triplet states. That is why triplets are important. Once the molecules are excited, many photophysical processes can occur. When the molecule that is in the ground state is excited, the photon energy will bring it into the S1 electronic state at a higher vibrational level. Once we have the absorption Kabs, the molecule can trickle back down from the maximum line in the S1 to the minimum of the S1 state. It does that by going down the vibrational levels and therefore, vibrations are created in the molecule. That is how the molecule loses its energy. This process is referred to as internal conversion (kic) because it remains within the same spin manifold and possibly within the same excited states. Then from the minimum of S1, the molecule can also decay back to the ground state without the emission of a photon (non-radiativeally). This is not a good thing when we are interested in light emission. It could also decay back to the ground state by emitting a photon, which is referred to as a fluorescence phenomenon (kfl). All these processes have rates that are generally typical for conjugated molecules.
Starting at S0 a photon is absorbed, spin multiplicity is conserved, and the electron gets into S1. Then in some instances, a crossover to the triplet manifold T1 can occur. This crossover to the triplet manifold is referred to as intersystem crossing. The Kisc shown between S1 and T1 represents the intersystem crossing. The intersystem crossing can cause molecule to trickle down back to the bottom of T1, thus intersystem crossing is followed by internal conversion. At the bottom of the T1 state, the molecule usually lives for a pretty long time. Since it is metastable, the probability of it descending back to the ground state is small but even so eventually happens. If it occurs radiadivally then a phosphorescence can be produced. It could also come down from T1 via emission of vibrations through internal conversion. Molecules that are efficient enough to be used in a display must have very large rates for fluorescence or phosphorescence. With a molecule such as naphtaline, a flat hypercarbon, the probability of this fluoresence occuring is extremely small. But there is a way to increase the probability.
Singlets and Triplets
It is important to know that states refer to the multi-electron system. We will make an approximation and simply look at the orbital levels, HOMO, LUMO and so on. In a large number of cases, the first excited state can mainly be described by the promotion of an electron from the HOMO level to the LUMO Level. The first energy level diagram of the four shows a spin of +1/2 in the HOMO and a spin of +1/2 in the LUMO. (This doesn’t mean that this first case always occurs in excitation; it is just possible to have this situation at some point.) In this case, the two spins are aligned and the total spin number is 1. This case is one of the triplet states. Another triplet state can occur like the 2nd energy diagram shown on the right of the first. It is also possible to have opposite spins. The third diagram shows a situation where the spin is +½ or what I refer to as α on the HOMO, and the spin is -½ or β on the LUMO. The fourth diagram shows the reverse of the third: there is a -1/2 β on the HOMO and +1/2 α on the LUMO. The first two situations and diagrams represent pure quanta-mechanical spin states. However, the last two are not; only their combination is. Therefore, there are two ways to obtain a triplet state. One way to have both electron spins to have the same direction. The way is to take the linear positive combination of the last two diagrams. This is done on the slide with the proper normalization factor; the α for electron 1 and β for electron 2 plus the fourth diagram which has an α for electron 2 and β for electron 1. This defines the third triplet configuration.
Thus, the triplet state has a multiplicity of three with magnetic numbers of +1 (first diagram), -1(second diagram), and 0(combination of the last two diagrams), and total spin number in all cases is equal to 1. The singlet state is the subtraction of those two spin configurations in the last two diagrams. Usually, when referring to a singlet state, there is one spin like with an upward direction and the other spin has a downward direction. However, the quantum mechanical situation is a bit more complex than what this leads you to believe. For the triplet, the two spin configurations are easy to pinpoint but the third one only exists in combination. Remember that the third spin configuration diagram and the last spin configuration do not correspond to pure states. Their plus and minus combination is necessary to get to the actual spin state.
External Links
| Previous Topic | Return to Absorption and Emission Menu | Next Topic |