Quantum-Mechanical Theory of Molecular Polarizabilities

Quantum-Mechanical Theory of Molecular Polarizabilities up to Third Order

The literature refers to first order, second order and third order polarizabilities. You may also see “first order hyperpolarizability “ which is the same thing as second order polarizability. These conventions may be confusing.

Our goal is to be able to relate the chemical structure and the nature of the pi-conjugated backbone, and the nature of donor and acceptors to the to kind of non-linear response that can be measured or calculated.

The expression for dipole moment is simply the sum of all the point charges over all those point charges of the charge itself times the position of that charge.

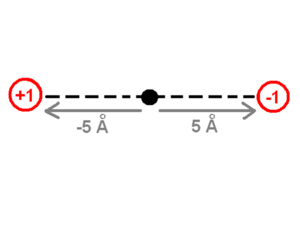
The drawing of the charges shows a point charge of +1 on the left side and a point charge of -1 on the right side. The origin of the system of coordinates is in the middle of these charges. The point charge of +1 is -5 angstrom away from the origin and the point charge of -1 is +5 Angstrom away on the x-axis. The first step to calculate the dipole moment is to multiply the charge +1 by the position -5 Angstrom for the +1 point charge, which will be -5eA (electron times angstrom). Then do the same for the -1 point charge (-1 * 5) which equals -5eA as well. Finally the sum of these values (-5eA + -5eA) -10eA, which corresponds to about -48 debyes, will be the dipole moment. The literature does not use the SI units of the dipole moment because the SI units use coulomb for the charge and meters for the distance which are macroscopic units. Instead, the dipole moment units use electron units and Angstrom (eA), or Debye.

<math>Cb \cdot m or Debye \approx 4.8 q(|e|) x d(A)\,\!</math>