Work Function of Metals

Work Function of Definition

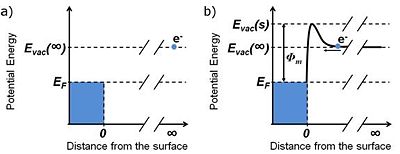
Let us consider an electron at rest in a vacuum at an infinite distance from a metal surface, as depicted in Figure 1a. The total energy, E_tot, of such an electron is equal to its potential energy, which can be defined after Cahen and Kahn as the vacuum level at infinity, E_vac(∞).. Let us supply the electron with some kinetic energy, E_k, and allow it to travel towards the surface. The total energy of the electron outside the metal can be expressed as the sum of its potential energy, E_V, and kinetic energy, E_k:

<math>E_{tot} = E_V + E_k\,\!</math> Equation 1

As the distance between the electron and the metal surface decreases the potential energy of the electron will increase, thus slowing it down, according to Equation 1 (see Figure 1b). If the kinetic energy is sufficiently large to overcome the potential barrier at the metal / vacuum interface the electron will go over the barrier and then will rapidly lose its potential energy due to the interaction with the positively charged ion lattice within the metal, resulting in the increase of kinetic energy. Once the electron is within the metal Equation 1 no longer holds as the interactions with other electrons and the ion lattice result in energy dissipation and thermal equilibration. The electron is now trapped within the metal.

A similar thought experiment can be performed in the opposite direction. Let us choose an electron from one of the highest occupied energy levels at the particular temperature of the system. The potential energy of this electron is approximately at the Fermi level, E_F. In terms of Fermi – Dirac statistics the Fermi level is defined as the energy at which the probability of finding an electron is 0.5 for a system at thermal equilibrium. For metals at room temperature the probability of finding an electron below the Fermi level is close to unity.I

The electron is then supplied with some kinetic energy, E'_k, sufficiently large to overcome the potential barrier existing at the metal surface. Right after escaping the metal, the greatly slowed-down electron has a potential energy which can be defined as the vacuum level close to the surface, E_vac(s).¹ The drop in the kinetic energy of the electron caused by the potential energy barrier is defined as the work function of the metal surface, φ_m: ^1,2

<math>\Phi_m = E_{vac}(s) - E_F\,\!</math> Equation 2

After escaping from the metal the electron is moving away further from the surface experiencing acceleration as the potential drops to the value of E_vac(∞).

Figure 1. a) Potential energy of an electron in vacuum at an infinite distance from a metal surface, E_vac(∞), and the Fermi level of the metal, E_F. b) Potential landscape the electron experiences along a travel path towards the metal surface (thick line). The difference between the electron energy just outside the metal surface, E_vac(s), and E_F defines the work function of the metal surface, φ_m = E_vac(s) - E_F.

It is important to describe the physical origin of the potential landscape illustrated in the above thought experiment. As already mentioned, the sharp potential drop the electron experiences when it enters the metal is related to the electrostatic attraction force between the negative charge of the electron and the positively charged ion lattice of the metal. However, at the vacuum / metal interface the electron experiences a potential energy barrier. This implies that in that region of space there must be a repulsive force that acts upon the electron. Indeed, the lack of positively charged metal ions on the vacuum side of the aforementioned interface causes a negative charge to exist just outside of the metal and, conversely, an uncompensated positive charge within the metal. The spilling of the electronic density outside of the solid causes a formation of a sheet of dipoles, which are often referred to as the surface dipoles.^1-3