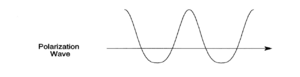Second-order Processes
Asymmetric Polarization
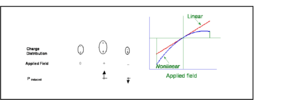
In second order non linear optics we are concerned with asymmetric polarization
This is a representation of what happens to a molecules that is asymmetric when an electric field is applied. A molecule with a dipole such as 4-nitro aniline has a charge distribution that leads to a dipole. One side is a donor (d) and an acceptor (a) with a pi conjugated system. The magnitude of the induced dipole will be greatest when the electric field is aligned so as to move the electron density towards the electron donor end of the molecule. In a symmetric molecule is there a linear polarizability shown as the straight line. The greater the charge the greater the induced dipole. In an asymmetric material there an nonlinear effect which makes it easier to polarize in one direction than the other, and increasing field has an exponentially increasing effect.
In the presence of an oscillating electric field a linear material will have an induced dipole that is in phase and has the same frequency as the applied field.
The application of a symmetric field (i.e. the electric field associated with the light wave) to the electrons in an anharmonic potential leads to an asymmetric polarization response. This polarization wave has flatted troughs (diminished maxima) in one direction and sharper and higher peaks (accentuated maxima) in the opposite direction, with respect to a normal sine wave.
It is possible to go back and find the sum of waves that would result in such a wave (fourier transform). In the case of a symmetric polarization it is simply the sine wave of the applied field.
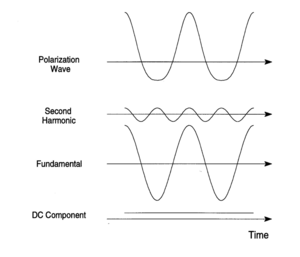
This asymmetric polarization can be Fourier decomposed (deconvoluted) into a static DC polarization component and components at the fundamental frequency superimposed with a second harmonic frequencies (at twice the fundamental frequency). This is a consequence of the material having second order non-linear properties.
As a consequence if you shine a laser at a non-linear optical material you can get light out of a different wavelength than the exciting source. In addition this emission can occur at a wavelength where the molecule is completely non-absorbing. This emission is not due to absorption / fluoresence. In second harmonic generation the light coming out can be twice frequency of the exciting source and the phenomena is tunable.
A laser of one frequency can be used to generate light of other frequencies. For example green light from a niodinum YAG laser (1064nm wavelength - green) can be directed on a non-linear optical crystal such as potassium dihydrogen phosphate and generate a second harmonic which is then used as a source for other experiments.
Since only the time averaged asymmetrically induced polarization leads to second-order NLO effects, only molecules and materials lacking a center of symmetry possess them.
Fourier Analysis of Asymmetric Polarization Wave
This asymmetric polarization can be Fourier decomposed (deconvoluted) into a static DC polarization component and components at the fundamental frequency superimposed with a second harmonic frequencies (at twice the fundamental frequency). This is a consequence of the material having second order non-linear properties.
As a consequence if you shine a laser at a non-linear optical material you can get light out of a different wavelength than the exciting source. In addition this emission can occur at a wavelength where the molecule is completely non-absorbing. This emission is not due to absorption / fluoresence. In second harmonic generation the light coming out can be twice frequency of the exciting source and the phenomena is tunable.
A laser of one frequency can be used to generate light of other frequencies. For example green light from a niodinum YAG laser (1064nm wavelength - green) can be directed on a non-linear optical crystal such as potassium dihydrogen phosphate and generate a second harmonic which is then used as a source for other experiments.
Since only the time averaged asymmetrically induced polarization leads to second-order NLO effects, only molecules and materials lacking a center of symmetry possess them.
Expression for Microscopic Nonlinear Polarizabilities
The linear polarizability is the first derivative of the dipole moment with respect to electric field. In non-linear optical effects the plot of induced polarization vs applied field can be corrected using higher corrections with a Taylor series expansion, including the second derivative of the dipole moment with respect of field times the field squared with a single electric field, or higher order terms using the third derivative of dipole moment vs field the field cubed. Mu is the total dipole moment in the molecule which is a sum of the static dipole plus several field dependent term.
- <math>\mu = \mu_0 + (\partial \mu / \partial E_i)_{E0}E_j + 1/2 (\partial^2 \mu_i / \partial E_jE_k)_{E0} E_jE_k+ 1/6(\partial^3\mu_i / \partial E_jE_kE_i\,\!</math>
The terms beyond aE are not linear (they have exponential terms) in E and are therefore referred to as the nonlinear polarization and give rise to nonlinear optical effects. Note that Ej, Ek, and Ej are vectors representing the direction of the polarization of the applied field with respect to the molecular coordinate frame. Molecules are asymmetric have different polarizabilities depending the direction of the applied electric field.
Alpha is linear polarizability Beta is the first hyperpolarizability ( a third rank tensor with 27 permutations although some are degenerate) Gamma is the second hyperpolarizability, responsible for third order non linear optics.
Alpha is the second derivative of the dipole moment with respect to field is also the first derivative of the polarizability with respect to field. Beta is the first derivative of polarizability with respect to field, and gamma is the first derivative of the first hyperpolarizability with respect to field.