Sigma and pi Orbitals
Return to Molecular Orbitals Menu | Next Topic Polarization is an important concept in designing electro optical materials.
Mechanisms for polarization
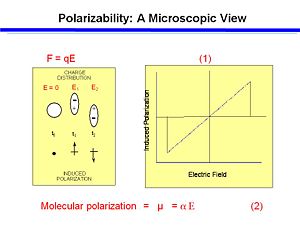
If you have any mechanism to apply an external electrical field this may lead to polarization of the molecules. In electronic polarization the field pulls electrons more than it repells the nucleus because electrons are far lighter than the protons and neutrons. The timescale for polarization of a atom due to a field is 10 -15 seconds. This is about as fast as you can do things.
If two atoms with unequal electronegavity are bonded the molecule will have a dipole moment. A vibration of the atoms results in a change in the position of the nuclei and the electrons follow the nuclei. This happens on a timescale of picoseconds. Infrared leads to vibrations of molecules. The reciprocal of the frequency of IR has a time constant of 100 femptoseconds.
You can have molecules that already have a dipole moment and place them in an electronic field the molecules will align. This time constant for this rotation is in the area of 10s of nanoseconds. Microwave radiation can be used to cause rotations in molecules.
If there are ions in the presence of an electric field there will be a bulk motion. If there is an oscillating electronic field it needs to be matched to the timescale of the polarization mechanism. Only those components that react as fast or faster than the frequency will make a contribution to the bulk polarization of the material. The following animation demonstrates these four types.
<swf width="500" height="400">http://depts.washington.edu/cmditr/media/01 Polarization Mechanisms.swf</swf>
Here is an hydrogen atom in an oscillating electric field. The atom is is oscillating as the electrons are being displaced and the energy levels are changing.
In an atom with π orbitals there is more polarizability in the π orbitals than in the σ orbitals. Dyes are typically π conjugated compounds because π orbitals are more polarizable in the visible spectrum.
Linear polarizability
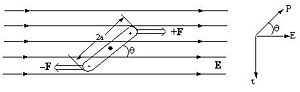
Molecules that have a dipole moment will orient in an electric field. These are known as second order non-linear material. The force that is on the system is a torque that is related to angle between dipole and the electric field, and upon the magnitude of the field and the dipole. If the molecule is aligned with the field it will not feel a torque. If it oriented at 90 degrees it will feel a substanstial torque.
Dipole is vector quantity, it has a magnitude and a direction. An opposite field will induce a dipole in the opposite direction.
If you plot dipole moment against the electric field you get a straight line. The slope (α) of the line for the function is the linear polarizability. A higher α means a greater amount of polarization for the same amount of applied field.
<math>\mu = \alpha \Epsilon\,\!</math>
Anisotropic Polarizability
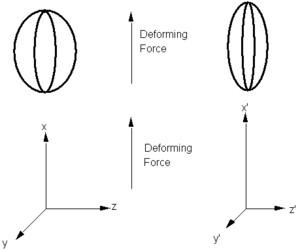
An organic molecule, 2-4 Hexadi-ine has two triple bonds and single bonds between two of the carbons. The triple bonds form a cylinder of electrons. If you apply and electic field along the long axis of the cyclinder you will get a larger induced dipole moment. If you assume that the polarizability at 90degrees to the axis is negible compare to the that of the along the long axis then electrons are going to move along the axis only. The interaction of the electric field with the electrons is greatest in long direction, and becomes zero at 90 degrees. This can be described as a dot product, a cosine function. An oscillating field will cause electrons to move up and down along the long axis and creates an induced dipole. Molecules that are oriented at 45 degree angle will have some induced dipole due to the applied field. This induced field can be used with cross polarizers to allow or not allow light to pass through the material.
Tensor calculation
To describe the polarizability of this kind of molecule you have to use a tensor to describe all the components of polarizability. It is possible to apply an electric field along y but induce a dipole moment along y. Each entry of the tensor is a component of the polarizability.
<math>\begin{pmatrix} \mu_x\\ \mu_y\\ \mu_z \end{pmatrix} = \begin{pmatrix} \alpha_{xx}& \alpha_{xy}& \alpha_{xz} & \\ \alpha_{yx}& \alpha_{yy}& \alpha_{yz} & \\ \alpha_{zx}& \alpha_{zy}& \alpha_{zz} & \end{pmatrix} = \begin{pmatrix} E_x \\ E_y \\ E_z \end{pmatrix} \,\!</math>
You can calculate the degree of polarization in any direction with the tensor product;
<math>\mu_x = \alpha_{xx} E_x + \alpha_{xy} E_y + \alpha_{xz} E_z\,\!</math>
Consider the electric field is a deforming force and the dipole moment is the deformation. The balloon can be stretched in one direction resulting in changes in the other dimensions. A balloon could be isotropic meaning it would be equally easy to stretch in all directions. Or it could have fibers built in that would limit the deformation along one axis. An electric field from any direction can induce a dipole in any direction. The components along the diagonal tend to be the strongest. It is possible to have more than one electric field applied (along x and y). To describe this situation you actually need a 3 x 3 x 3 (third rank) tenso, a matrix with 27 components. You could even have 3 electric fields with 81 components.
Dielectric Constant
In bulk materials, the linear polarization is given by:
<math>P_i(\omega) = \sum_{ij}\chi_{ij}(\mu)\E_j(\omega)\,\!</math> (4) where <math>\chi_ij(\omega)\,\!</math> is the linear susceptibility of an ensemble of molecules
Note that the vectorial and tensor aspects of E and <math>\chi\,\!</math> have been ignored to simplify notation.
The total electric field (the "displaced" field, D) within the material becomes:
<math>D = E + 4\piP = (1 + 4_{\pi\chi})E \,\!</math> (5)
<math>P = \chiE\,\!</math> (Equation (4)), <math>4_{\pi\chi}E\,\!</math> is the internal electric field created by the induced displacement (polarization) of charges.