Perturbation Theory

Hellman-Feynman Theorem

The Hellman-Feynman Theorem, which expresses the dipole moment as minus derivative of the energy of the system with respect to the field. This equation expresses the response of a molecule which is 2nd order in terms of the energy of the molecule and first order in terms of the dipole moment of the molecule (1st order or 2nd order with respect to the field).

<math>\overrightarrow {\mu} = - \frac {\delta E} {\delta \overrightarrow{F}}\,\!</math>

<math>\overrightarrow{\mu} = \overrightarrow{\mu^\circ} + \alpha \overrightarrow{F} + \frac {1} {2!} \beta \overrightarrow{F}\overrightarrow{F} + \frac {1} {3!} \gamma \overrightarrow{F}\overrightarrow{F}\overrightarrow{F}\,\!</math>

<math>\frac {\delta \overrightarrow{\mu}}{\delta \overrightarrow{F}} = \alpha + \beta \overrightarrow{F} + \frac {1} {2!} \gamma \overrightarrow{F}\overrightarrow{F} + ...\,\!</math>

Stark Energy Expression

Alpha is the linear polarizability or the first order polarizability. It describes how the molecule responds in terms of the modification of its ground state energy or of its dipole moment, in the presence of the field at the limit where the field goes to 0. Thus, α can be cast either as the 1st order derivative of the dipole moment with respect to the field when the field tends to 0 or minus the 2nd order derivative of the ground state energy of the molecule with respect to the field when the field goes to 0.

<math>\alpha = \left( \frac {\delta\overrightarrow{\mu}}{\delta \overrightarrow{F}}\right) \overrightarrow{F} \rightarrow 0 \,\!</math>

<math>= - \left( \frac {\delta^2 \overrightarrow{\mu}}{\delta \overrightarrow{F}^2}\right) \overrightarrow{F} \rightarrow 0 \,\!</math>

Beta is the 2nd order derivative of the dipole moment with respect to the field when the field goes to 0. Beta will be referred to as the 2nd order polarizability of the molecule. This can also be derived from the stark energy expression which is the 3rd order derivative of the energy with respect to the field when the field tends to 0.

<math>\beta = \left( \frac {\delta^2 \overrightarrow{\mu}}{\delta \overrightarrow{F}^2}\right) \overrightarrow{F} \rightarrow 0 \,\!</math>

<math>= - \left( \frac {\delta^3 \overrightarrow{\mu}}{\delta \overrightarrow{F}^3}\right) \overrightarrow{F} \rightarrow 0 \,\!</math>

Lastly, the γ term corresponds to the 3rd order derivative of the dipole moment or minus the 4th order derivative of the energy with respect to the field at the limit where the field goes to 0. γ will be referred to as the 3rd order polarizability of the molecule.

<math>\gamma = \left( \frac {\delta^3 \overrightarrow{\mu}}{\delta \overrightarrow{F}^3}\right) \overrightarrow{F} \rightarrow 0 \,\!</math>

<math>= - \left( \frac {\delta^4 \overrightarrow{\mu}}{\delta \overrightarrow{F}^4}\right) \overrightarrow{F} \rightarrow 0 \,\!</math>

Stark energy describes the evolution of the energy of a system of particles in the presence of an electric field F. In the Stark energy expression, γ corresponds to a 4th order term. However the in common terminology α is referred to as the linear polarizability, β the 2nd order polarizability, and γ the 3rd order polarizability. The Hellman-Feynman Theorem is the origin of these terms. Here it is presented as a Taylor series expansion, sometimes one uses a power series expansion.

<math>

E_g = E^\circ_g = \overrightarrow{\mu}^\circ \overrightarrow{F} - \frac {1} {2!} \alpha \overrightarrow{F}\overrightarrow{F} - \frac {1} {3!} \beta \overrightarrow{F}\overrightarrow{F}\overrightarrow{F} - \frac {1} {4!} \gamma \overrightarrow{F}\overrightarrow{F}\overrightarrow{F}\overrightarrow{F}\,\!</math>

<math>= E^\circ_g - \overrightarrow{\mu}\overrightarrow{F}\,\!</math>

Electric dipole approximation

The stark energy expression states that the ground state energy of the molecule in the presence of the field is the ground state energy in the absence of the field minus μF. Thus, μF is considered the interaction between the field and the molecule. The electric dipole approximation is that only the electric field component of light influences dipole moment. The magnetic component is ignored. In most instances in the literature, this approximation is assumed but not stated. The expression for the dipole moment is expressed as :

<math>\mu^\circ + \alpha F + \beta F^2 ... \,\!</math>

and so on, without paying any attention to where that expression comes from.

<math>- \overrightarrow{\mu}\overrightarrow{F}\,\!</math>

in dimensional analysis:

<math>\mu \equiv\,\!</math> charge * distance

<math>F \equiv\,\!</math> volt/distance

<math>\mu F \equiv\,\!</math> charge * volt :<math>\equiv\,\!</math> energy

After the electric dipole, the next two terms are the electric quadrupole and the magnetic dipole. 99% of the time only the electric dipole is considered. This represents the difference in energy between the perturbed state and the unperturbed state of the molecules. Thus, this must have an energy dimension. μ is the dipole moment which is the charge times the distance, and the electric field is volt over distance. When you multiply these terms, the expression has the dimension charge times volt or ev, and ev is an energy unit. This will be used in perturbation theory.

The stark energy expression states that the ground state energy of the molecule in the presence of the field is the ground state energy in the absence of the field minus μF. Thus, μF is considered the interaction between the field and the molecule. The electric dipole approximation is that only the electric field component of light influences dipole moment. The magnetic component is ignored. In most instances in the literature, this approximation is assumed but not stated. The expression for the dipole moment is expressed as

<math>\mu^\circ + \alpha F + \beta F^2...\,\!</math>

and so on, without paying any attention to where that expression comes from.

<math>\overrightarrow{\mu} = e \sum(i) \overrightarrow{\pi}_i 9i\,\!</math>

After the electric dipole, the next two terms are the electric quadrupole and the magnetic dipole. 99% of the time only the electric dipole is considered. This represents the difference in energy between the perturbed state and the unperturbed state of the molecules. Thus, this must have an energy dimension. μ is the dipole moment which is the charge times the distance, and the electric field is volt over distance. When you multiply these terms, the expression has the dimension charge times volt or ev, and ev is an energy unit. This will be used in perturbation theory.

Perturbation theory

The perturbation theory will not be discussed at the quantum- mechanics level. The energy of the ground state of the system is the energy for the unperturbed system. Perturbation can be observed at different orders. At first order, the perturbation is referred as w. If that perturbation is the impact of the electric field of the light in the electric dipole approximation, the perturbation can be expressed as minus μF.

At the first order, the perturbation is operating on the unperturbed wave function of the ground state. Perturbation theory involves modification of systems due to the perturbation of all the wave functions for the unperturbed system. At first order, the perturbation is simply acting on the ground state wave function. Then it is integrated over space and the complex conjugate is taken. At second order, the wave functions of the excited state are taken into account to describe the modification of the system. An unperturbed system has a well defined wave function for the ground state and well defined wave functions for the excited states. The perturbed system is described on the basis of the wave functions of the unperturbed system.

<math>=\int \Psi* e \overrightarrow{\pi} \Psi dr\,\!</math>

<math>E_g = E^\circ_g + \langle \Psi_g | w | \Psi_g \rangle + \sum_p \frac {\langle \Psi_g | W | \Psi_p \rangle \langle \Psi_p | W | \Psi_g \rangle + ...}{ E^\circ_p - E^\circ _g}\,\!</math>

<math>E_g = E^\circ_g -\overrightarrow{\mu ^\circ} \overrightarrow{F} - \frac {1} {2!} \alpha \overrightarrow{F}^2 - ....\,\!</math>

<math>W = - \overrightarrow{\mu} \overrightarrow{F}\,\!</math>

In terms of non-linear optics, the perturbation theory expressions will show what the excited states are in your isolated molecule that will contribute to the linear polarizability, 2nd order polarizability, or the 3rd order polarizability and allow you to pinpoint exactly what excited states do play a major role in your optical response.

The complete set of wave functions for the unperturbed state will form the basic set for the perturbation expressions. In principle this includes all excited states. The 2nd order term in terms of perturbation and will correspond to α, the linear polarizability. In most conjugated systems, only the first excited state needs to be examined. This will often be the case for α and π-conjugated systems as well as for β. But not for γ in which two or more excited states must be taken into account. However, the number of states that need close attention can be heavily restricted.

<math>E_g = E_g^\circ - \underbrace{\langle | \Psi_g | W | \Psi _g \rangle} \overrightarrow{F} + \,\!</math>

<math>\overrightarrow{\mu^\circ}\,\!</math>

<math>\underbrace{\sum_p \frac {\langle \Psi_g | e \overrightarrow{r} | \Psi_p \rangle \langle \Psi_p | e \overrightarrow{r} | \Psi_g \rangle \overrightarrow{F}\overrightarrow{F}}{ E^\circ_p - E^\circ _g}}\,\!</math>

<math>-\frac {1} {2!}\alpha\,\!</math>

A one to one correspondence can be made between the terms in the stark energy expression and the perturbation theory expression when the perturbation is minus μF.

As a side note, as you go to higher orders, things will look a bit more complicated because there are more summations over excited states. For example in 3rd order, there will be a double summation over excited states. In 4th order, there will be a triple summation over excited states. But it will always be products of matrix elements of this kind at the numerator, and the differences in energies of the states for the unperturbed molecule will be in the denominator. The expressions look more complex but by looking at the terms individually, notice that the same kind of terms come up. P is summation over all excited states

- μF is the electric dipole approximation. The operator expression, μ is the unit electric charge times the position, which is the dipole moment. The electric field does not do anything to the wave functions of the unperturbed state. This expression here? is the expression of the dipole moment for the ground state Φ_g is the wave function of the ground state in the unperturbed state, which is simply μ ^&o;. At first order, the goal is to find the possible dipole moment. If there is a central symmetry, there won’t be any permanent dipole moment of the molecule. If there is a permanent dipole moment, there will be an interaction between that permanent dipole moment and the external field. At second order, the expression includes the summation over all the excited states p. Here perturbation is replaced by its expression er. Since this deals with the wave functions of the unperturbed system, the electric field is outside. This shows a transition dipole between the ground state and excited state p. and the transition dipole between excited state p and the ground state. These terms are equal. They are the exact same transition dipole. The denominator is the square of the transition dipole between the ground state and excited state p.

The numerator is the difference in energy between the ground state energy and the excited state energy. Finally, by closely examining the stark energy expression, a connection can be made between the term that is linear in the field, μ^oF minus ½ α. This shows the expression for α as a function of this perturbation expression.

<math>\alpha=2 \sum_p \frac {\langle \Psi_g | e \overrightarrow{r} | \Psi_p \rangle \langle \Psi_p | e \overrightarrow{r} | \Psi_g \rangle \overrightarrow{F}\overrightarrow{F}}{ E^\circ_p - E^\circ _g}\,\!</math>

<math>=2 \sum \frac {M_{gp} ^2} {E^\circ _{gp}}\,\!</math>

In this expression there is no longer a minus sign because the denominator is reversed; E of Pnot – E of gnot.

Now there is a compact expression where α is equal to 2 times the summation over all excited states of transition dipole with state p times transition dipole with state p over the transition energy. Taking into account of the perturbation theory, α, the linear polarizability, can be described as a sum over all excited states of the square of the transition dipole between the ground state and the excited state, over the transition energy from the ground state.

Error creating thumbnail: Unable to save thumbnail to destination

A pictorial description shows the process of going from the ground state to excited state p and that is a transition dipole between g and p. There is also another transition dipole when coming back from p to g. That is why the expression for α shows transition dipole squared. As previously explained, the expressions for β will look more complex due to the double summations over excited states. The expression for γ will look even more complex due to the triple summations over excited states. However for all instances, the numerator will always be products of transition dipoles and the denominator will contain the transition energy. In the literature, the perturbation theory expressions are also referred to as “sum over states expressions” the expression contains the sum over all excited states.

A few important questions include “What is the impact of the perturbation on the energy of the system?” and “Would it stabilize or destabilize the system when looking at the perturbation at different orders?”. It is crucial to understand the differences and variations in conventions. Suppose you want to calculate the dipole moment of the molecule using two programs. First, you input the geometry of the molecule exactly in the same way for both programs. Then, you run the calculation. One program gave a dipole moment of +1.3 Debye, but the other program gave you a dipole moment of -1.3 Debye. Why is there a difference? The difference occurs because the conventions are different for chemists and physicists.

<math>= - \left( \frac {\delta^4 \overrightarrow{\mu}}{\delta \overrightarrow{F}^4}\right) \overrightarrow{F} \rightarrow 0 \,\!</math>

<math>\overrightarrow{\mu}= \overrightarrow{\mu^\circ} + \alpha \overrightarrow{F}+ 1/2 \beta \overrightarrow{F}\overrightarrow{F} +1/6 \gamma \overrightarrow{F}\overrightarrow{F}\overrightarrow{F} ...\,\!</math>

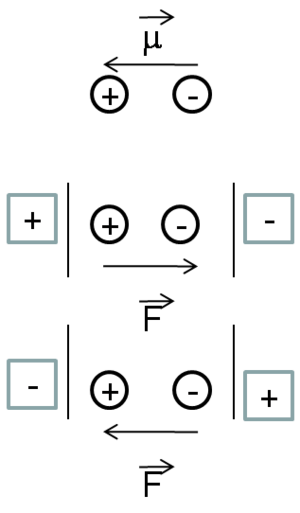
Before physicists discovered the nature of electrical charge and electrical current, there wasn’t a way to identify whether the charge carriers were positively or negatively charged. Therefore, they made an assumption that it was positive charge that moves . But it turned out that their guess was wrong. We now know, it is the negatively charged electrons that provide electrical conductivity in metals or materials. Thus, in many of the conventions, physicists traditionally observe how the positive charge moves. Whereas chemists look at the displacement of an electron. As a result, the dipole moment can be written as going from left to right if you have a donor-acceptor molecule.

Suppose a quasi one dimensional D-conjugated bridge -A molecule with z the long axis and then apply an external field along z.

<math>\overrightarrow{\mu}^\circ\,\!</math>

<math>\rightarrow\,\!</math>

D ----- conjugate -------- A

<math>\rightarrow\,\!</math> :<math>\overrightarrow{F}_x\,\!</math>

<math>\leftarrow\,\!</math>

It can also be written, as going from right to left. Suppose that we have a donor acceptor molecule with a conjugated bridge between the two. In linear quasi- 1-demensional type molecules, the whole optical or non-linear optical responses will occur along the axis Z of the molecule.

Stabilization

Assume you have molecule that has a positive pole and a negative pole. You can place an electric field along the main axis in two directions. At the first order you will only observe the permanent dipole moment of the molecule and its interaction of the field; thus you have a permanent dipole moment period. You have a plus and a minus. It is also important to know which situation, the one on the top or the one on the bottom, will be more stable. As a matter of fact, the one at the bottom will be the most stable situation. This is because when you have two dipole moments on top of one another, the anti-parallel? situation will be much more favorable then the parallel situation. In anti-parallel situation the positive charge is stabilized by the negative pole of the electric field and the negative charge is stabilized by the positive pole. Where as in the parallel situation there is a destabilization. Therefore, independently from the conventions in terms of the electric field and the dipole moment, it is clear which situation will lead to a net stabilization of the energy of the system and which one will lead to a destabilization.

At first order, nothing changes within the molecule.

At second order you will have a flux of electrons towards the left to counteract the external field in the lower case, and in the upper case you will have a flux of electrons toward the right. Thus, the system will always respond in a way to stabilize itself. At third order, it gets more complicated.

First order energy term

<math>E(\overrightarrow{F}) - E^\circ = - \overrightarrow{\mu^\circ} \overrightarrow{F}\,\!</math>

<math>= - \overrightarrow{\mu}_z ^{ \circ}- \overrightarrow{F}_z\,\!</math>

There is stabilization if  :<math>\overrightarrow{F}_z\,\!</math> is parallel to :<math>\overrightarrow{\mu}^\circ\,\!</math>

There is destabilization if  :<math>\overrightarrow{F}_z\,\!</math> is anti-parallel to :<math>\overrightarrow{\mu}_z^{\circ}\,\!</math>

In other words, with the indicated conventions, stabilization will occur if the field is parallel to the dipole moment and destabilization will occur in the opposing case. But again, that depends on the conventions chosen for the field and dipole moment. Remember that at first order in the field ( the linear term of the energy expression) only the interaction between the permanent dipole moment, is examined. However, at higher orders, we examine how the system responds to the external field on the molecule. As a result, we look at the polarizabiliy, or in the case of alpha the linear polarizability. In perturbation theory the second order term gives the stabilization.

This can easily be seen from the previous expression. Alpha is a summation over all excited states of the squares of the transition dipole, which makes it positive. The transition energy going from the ground state will always be positive by definition of the ground state.

Second order energy term

<math>- \frac{1}{2} \alpha_{zz} \overrightarrow{F}_z \overrightarrow{F}_z\,\!</math>

Alpha is positive and we multiply by F times F, which will be positive. Therefore, the whole second order term leads to a stabilization of the system.

Think back about the simple example shown previously. At first order, nothing changes within the molecule. At second order, look at the response of the molecule to the external field. What will happen here? What will happen is that you will have a flux of electrons towards the left to counteract the external field, and here you will have a flux of electrons toward the right. Thus, the system will always respond in a way to stabilize itself.

Alpha is a tensor of rank two and there are nine tensor components for alpha. Beta is a tensor of rank three. Since each of these indices can be x y z, there will be a possible of 27 tensor components.

third order energy term

<math>- \frac{1}{6} \beta_{zzz} \overrightarrow{F}_z \overrightarrow{F}_z \overrightarrow{F}_z\,\!</math>

There is stablilization or destablization depending on whether :<math>\overrightarrow{F}_z\,\!</math> is parallel or antiparallel to the vectorial part of β, and depends on the sign of β which depends on Δ μ _eg

In a two state model expression, β depends very much on the difference in state dipole moment between the ground state and the active excited state. Β will be positive if that active excited state has a dipole moment that is larger than the dipole moment in the ground state, and β will be negative if the dipole moment in the excited state is smaller than in the ground state. This is an easy way of understanding the variation in the sign of β.

Fourth order energy term

<math>- \frac{1}{24} \gamma_{zzzz} \overrightarrow{F}_z \overrightarrow{F}_z \overrightarrow{F}_z\overrightarrow{F}_z\,\!</math>

This is stabilizing if γ is >0 and destabilizing if γ is <0

For fourth order, in this case, the field components would lead to a positive term by necessity. Thus, we will have either stabilization if γ is positive or destabilization if γ is negative. This is consistent with the process called the self-focusing of light in the material with positive γ. If you shine a high intensity laser light into a molecule that has a very large positive γ response, the beam will self-focus. The system tends to go to higher local fields and therefore obtain a larger stabilization by focusing the light. Where as a negative γ leads to a defocusing of your light. This property can be use for protection from high intensity light.

Gamma is a tensor of rank four and there will be 81 tensor components. When looking at extended π conjugated molecules, (quasi 1-dimensional) the components along the long axis of the molecule will dominate everything. However, with molecules that become more complex in shape there are a number of components that can become important as well. Also, there are symmetry relationships among those components. In the literature on non-linear optics, there is something referred to as Climan symmetry that is based on the point groups of the different molecules that gives the relationship between the different tensor components. However, here we are mostly concerned with at the α_zz component, the β_zzz, or γ_zzzz What will be provided is a difference between the global value and the tensor component along the main axis. It is difficult to know whether the third order term leads to stabilization or destabilization because β could be positive or negative. Also, the combination of the three field terms can be positive or negative so it really depends.

Dipole changes

We can also look at what happens to the dipole moment. In the case of the α, the permanent dipole can be zero if we have a centrosymmetric molecule or it can be any value depending on the nature of the molecule. If it is non-centrosymmetric there will be an increase or decrease depending on the direction of the field at first order.

<math>\overrightarrow{\mu} = \overrightarrow{\mu^\circ} + \alpha \overrightarrow{F} = \overrightarrow{\mu^\circ_z} + \alpha \overrightarrow{F_z}\,\!</math>

First order: The dipole increases or decreases according to whether F_z is parallel or antiparallel to :<math>\overrightarrow{\mu^\circ_z}\,\!</math>

Second order:

The change depends on how the field is aligned with respect to the permanent dipole moment. At the next order FF is always positive so dipole it will be decided by the value of β. The sign of β can often be related to the difference in dipole moment between the ground state and the active excited state. If there is an increase in the dipole moment going from the ground state to the excited state, β will be positive. That excited state now contributes to the description of the system because with a larger dipole moment, it is reasonable to assume that the μ of the system will increase. The opposite will occur for a negative β. All these considerations will become clearer when the perturbative expressions for β and γ are discussed in detail.

<math>1/2 \Beta : \overrightarrow{F} \overrightarrow{F}\,\!</math>

In the context of the two state model, β has a sign of :<math>\Delta \mu_{eg}\,\!</math>

<math>\beta >0 : \mu \uparrow\,\!</math>

<math>\beta <0 : \mu \downarrow\,\!</math>

Third order For the impact of γ, the dipole moment depends on the sign of γ and the field alignments in the expression of the dipole moment. There will be three fields that will play a role.

Calculation of polarizabilities

Polarization of a medium due to an electric field.

In spite of the different conventions used to look at the physics of the system, it is good enough to just look at what the external field with respect to the permanent dipole moment does. Papers in the field of non-linear optics, especially for inorganic materials, often look at the macroscopic polarization that occurs when the field is applied. Since the experimentalists are not concerned with the possible derivations that are necessary when calculating α, β, γ, they often use an expression that is a power series expansion instead of a Taylor series expansion.

This expression of the polarization of the medium corresponding to the possible permanent polarization when the material is non-central symmetric. The expression contains a first order term which is the first order electrical susceptibility. Remember, the :<math>\chi^{(1)}\,\!</math> is a tensor; there will be 9 tensor components there. That is the equivalent of α for the microscopic scale.

<math>\overrightarrow{P} = \overrightarrow{P_0} + \chi^{(1)} \overrightarrow{F} + \chi^{(2)} \overrightarrow{F}\overrightarrow{F} +\ chi^{(3)} \overrightarrow{F}\overrightarrow{F}\overrightarrow{F} +\,\!</math>

<math>\chi^{(1)}\,\!</math> is the first order electrical susceptibility (second rank tensor).

<math>\chi^{(2)}\,\!</math> is the first order electrical susceptibility (third-rank tensor).

<math>\chi^{(3)}\,\!</math> is the third order electrical susceptibility, and so on.

Only :<math>\chi^{(1)}, \chi^{(2)}, \chi^{(3)}\,\!</math> will be considered, although experimentally there are people that have shown :<math>\chi^{(5)}, \chi^{(6)}\,\!</math> processes that are very specific.

Molecular materials at the microscopic level

<math>\overrightarrow{\mu} = \overrightarrow{\mu_0} + \alpha \overrightarrow{F} + \beta \overrightarrow{F} \overrightarrow{F} + \gamma \overrightarrow{F}\overrightarrow{F}\overrightarrow{F} + ...\,\!</math>

where

<math>\alpha\,\!</math> is first order polarizability

<math>\beta\,\!</math> is the secord order polarizability or first order hyperpolarizability

<math>\gamma\,\!</math> is the third order polarizability or second order hyperpolarizability

This is the corresponding expression for the dipole moment of a given molecule on the microscopic level. It is expressed in the power series expression. α is referred to as the polarizability. In the context of non linear optics, when looking at the β and γ terms, α can be more rigorously referred to as the first order polarizability. β is the second order polarizability or (some people prefer to use the expression) first order hyperpolarizability. γ is the third order polarizability or the second order hyperpolarizability. The reason why μ is expressed in both a power series expression and in a Taylor series expression is that most of the programs that make calculations use Taylor series expansion. However, the β or the γ that one calculates can differ from one program to another. It can differ by a factor of 2 for β, and by a factor of 6 for γ. Therefore, it is wise to also compare your calculated data with what is reported experimentally. Usually, experimentalists use a power series expansion. Thus, if they had done the calculation taking into account the Taylor series expansion, they will have immediately a difference by a factor of 2 or a factor of 6 with the experiment.

Stark Energy

Switching back to the Taylor series expressions. This shows the stark energy expression written in a more rigorous way taking into account for all the possible components of the field and for the tensor components of the α, β, and γ tensors.

<math>E(F) = E_0 - \sum_{i} \mu_{0i}F_i - \frac {1} {2!} \sum_{ij} \alpha_{ij} F_i F_j - \frac {1} {3!} \sum_{ijk} F_i F_jF_k - \frac {1}{4!} \sum_{ijkl} \gamma_{ijkl} F_i F_j F_k\,\!</math>

Dipole Moment

This shows a similar expression for the dipole moment. These two expressions are fully consistent with each other, given the Hellman-Feynman theory.

<math>\mu_i(F) = \mu_{0i} + \sum_j \alpha_ij F_j + \frac {1} {2!} \sum_{jk} \beta_{ijk} F_j F_k + \frac {1} {3!} \sum_{jkl} \gamma_{ijkl} F_j F_k\,\!</math>

<math>\mu_i = - \frac {\partial E(f)}{ \partial F_i}\,\!</math>

These expressions clearly show what was confirmed earlier regarding the tensors and its respective rank. For example, γ will be a tensor of rank 4 because you are looking at the impact on the i component of the dipole moment when applying a field along j, a field along k, or a field along L. That is the reason why the α, β, and γ contain all those tensor components.

<math>\alpha_{ij} = -\frac{ \partial ^2E(F)} {\partial F_i \partial F_j} = \frac {\partial ^1 \mu_i} {\partial F_j}\,\!</math>

<math>\beta_{ijk} = -\frac{ \partial ^3E(F)} {\partial F_i \partial F_j \partial F_k} = \frac {\partial ^2 \mu_i} {\partial F_j \partial F_k}\,\!</math>

<math>\gamma_{ijkl} = -\frac{ \partial ^4E(F)} {\partial F_i \partial F_j \partial F_k \partial F_l} = \frac {\partial ^3 \mu_i} {\partial F_j \partial F_k \partial F_l}\,\!</math>

Derivative Techniques

From those derivative expressions and the perturbative expressions, two types of calculations can be derived to evaluate the molecular polarizabilities from quantum-mechanical approaches. There is one major set of calculations that involve the derivation of either the energy or the dipole moment with respect to the external field. Those derivations can be done either numerically using methods referred to as finite-field methods, or analytically using Coupled Perturbed Hartree-Fock (CPHF) methods.

In a finite-field calculation, you take the interaction with the external field and put it into your Hamiltonian for the isolated molecule without any external perturbation. It has a kinetic term, a nucleic attraction term, a coulomb term, and exchange term. Now here, a fifth term is added to those present four terms. The fifth term expresses the interaction with your field. Several calculations are then made in which several values of the external field are taken into account. Then you do a numerical derivation of the dipole moments that you will have calculated as a response to the external field.

<math>H(\overrightarrow{F} = H_0 - \overrightarrow{\mu} \overrightarrow{F}\,\!</math>

The MO's are self-consistant with the eigenfunctions of :<math>H(\overrightarrow{F})\,\!</math>. What is interesting with those finite field methods is that since the perturbation interaction with the electric field is put into the Hamiltonian, the molecular orbitals that are derived are affected by that interaction. Then the α, β, γ tensor components are calculated by applying standard numerical procedures. Calculations are made with different values of the field. Different values of for dipole moment for the molecule are obtained. A numerical derivation is then made to get to α, β, and γ. For instance, two calculations are made for the α _ii component. The calculation is made with the field in one direction, and then again with the field in the opposite direction. It is important to have a value of the field that is large enough so that the molecule can respond and give a numerically accurate variation in the dipole moment. However, it should not be too large or the equivalent of a dielectric breakdown of your molecule will be obtained and the calculation will simply not converge. Therefore, it is crucial know what values of the fields are needed to evaluate.

<math>\alpha_ii = \frac {\partial\mu_i} {\partial F_i} = \frac {1}{2F_i} [\mu_i(F_i) - \mu_i(-F_i)]\,\!</math>

<math>

\gamma_{iiii} = \frac {\partial^3 \mu_i} {\partial F_i \partial F_i \partial F_i} = \frac {1} {48F_i^3} [\mu_i(3F_i)-\mu_i(-3F_i)- 3\mu_i (F_i)+ 3\mu_i (-F_i)]\,\!</math>

We pick a compromise value that is able to insure accuracy but also avoid divergence.

<math>F_i \approx 5 x 10^8 Vm^{-1}\,\!</math>

Coupled perturbed Hartree-Fock method

Another method that can be used to make those calculations is the analytical methods with analytical expressions for the variation of the energy with respect to the electric field.

<math>\beta_{ijk} = - \frac {\partial^3 E(F)} {\partial F_i \partial F_j \partial F_k}\,\!</math>

Perturbation techniques

Sum over state (SOS) method Besides making numerical or analytical calculations based on the derivation expressions, the perturbation theory expressions can also be used. This method is usually referred to as Sum Over States (SOS) method. This method was seen before for α. It is based on the perturbation expression for Stark energy terms which are related to optical nonlinearities based on their order in the field strength. α is calculated by evaluating the transition dipoles and the transition energies for all the excited states in the molecule.

You can look at the convergence of your values as a function of going over many excited states. However, it is important to understand that the higher energy you go, the larger the denominator becomes. Therefore, those terms will have smaller weight. Also, at very high excited states, the transition dipole will die down as well. For example, in the case of α the lowest excited states have the largest response.

<math>\alpha_{ij} = \sum_m \frac {<\psi_0|\mu_i | \psi_m > <\psi_m|\mu_j | \psi_0 >} {E_m- E_0}\,\!</math>

For the β terms, we have exactly the same components. However, the expression looks more complicated because it contains a double summation over excited states. That is transition dipole going from the ground state n to excited state to m. Then it goes from excited state m back to the ground state. The denominator has the transition energies. There is also a second term that goes over a summation over excited state due to the dipole moment starting in the ground state. Then there is a transition dipole going from the ground state to excited state n and then it comes back from n to the ground state, over transition energies. To generate these expressions go through the perturbation theory and work the second order and the third order perturbation theory expression, one can do so by placing the dipole (er), the dipole operator, and the electric field.

<math>\beta_{ijk} = \sum_n \sum_m \frac {<\psi_0|\mu_i | \psi_n > <\psi_m|\mu_j | \psi_0 ><\psi_m|\mu_k | \psi_0 >} {(E_n- E_0)(E_m- E_0)} - \sum_n \frac {<\psi_0|\mu_i | \psi_0 > <\psi_0|\mu_j | \psi_n ><\psi_n|\mu_k | \psi_0 >}{(E_m- E_0)(E_n- E_0)}\,\!</math>

The reason why it is interesting to evaluate the non-linear optic properties with those perturbation expressions (sum over state expressions) is because it pinpoints which excited states play important roles in optical and non-linear optical response. Another reason why they are heavily exploited is because the frequency dependence can easily be introduced with the response. With the finite-field method, it gets extremely complicated to introduce the frequency dependence.

The finite-field method is usually incorporated in many quantum chemistry packages. You just press key telling “calculate the molecular polarizabilites” and then you get numbers for those polarizabilites. However that is the problem; it only gives numbers and these are the static values where ω is equal to zero. It doesn’t provide an in depth understanding of what is occurring. There have been extensions to those methods that provide some kind of understanding regarding finite field methods of the local spatial contributions to the non-linear optical response. But it is a sophisticated approach that is not often used. Thus, in many instances, it more beneficial to use the sum-over states expression because it gives an idea of which electronic states matter. Also, frequency dependence can easily be introduced. The same thing can be done at the γ level.

<math>\beta^{SHG}(-2\omega;\omega \omega) = 1/2 \sum_n \sum \_m \frac {<\psi_0 | \mu_i | \psi_n><\psi_n|\mu_j|\psi_m><\psi_m |\mu_k|\psi_0>} {(\hbar\omega-(E_m-E_0))(2\hbar\omega-(E_m-E_0))}\,\!</math>

where

<math>(\hbar\omega-(E_m-E_0))\,\!</math> represents one-photon resonance

<math>(2\hbar\omega-(E_m-E_0))\,\!</math> represents two-photon resonance

Useful simplifications can be introduced if it is found that a single excited state dominates second order polarizability.

In the case of the first term, when the excited state m is different from excited state n, it will go from the ground state to m and then to n,. Then from n back down to the ground state. This slide shows the pictorial description of the products of the transition dipoles. However, if m is equal to n, you will go from the ground state to m, but then stay on m. Then you will come back down to the ground state. Staying on m if m is equal to n simply means that the state dipole moment of excited state m is being observed. Then there is a second term here that comes with a minus contribution where you have the state dipole in the ground state, and then you go from the ground state to m and then from m back to the ground state. This is the pictorial way that can describe the 3 different types of terms is found in the sum over states expression.

It is possible to take this expression, show that everything simplifies when approximating that there is a single excited state e that matters.If there is a single excited state e that provides the most significant contribution to the second order in non-linear optical response of the system, there are simplifications that can be obtained.

If one excited state e is dominant:

<math>\beta \approx \frac {<g|\mu|e> <e|\mu|e> <e|\mu|g>} {(E_e-E_g)}^2 - \frac {<g|\mu|g> <g|\mu|e> <e|\mu|g>} {(E_e-E_g)}\,\!</math>

<math>\approx \frac {|\mu_{eg}|^2 \Delta \mu_{eg}} {|\hbar \omega_{eg}|^2}\,\!</math>

This is known as a two state model which guided chromophore development for the last 30 years until we the theory of bond length alternation gave us better insight. From this simple expression, it became easier to know whether one needed a larger oscillator strength or a system that has a very large acentric coefficient as one goes from the ground state to an excited state. Most importantly, what one needs is a difference in dipole moment as large as possible between the ground state to the excited state. This makes sense because if one started with a dipole moment that is not very large in the ground state and in the excited state, one would generate a very large dipole moment, which indicates a separation of charges and a highly polarizable system.

Also, it is important to have small transition energies depending on the process that is being observed. For instance, in the early 90’s, there great interest in second harmonic generation in which the input frequency is doubled when output. This process was used for converting a red laser into a blue laser which was important until people developed lasers that could shine without doubling the frequency. In order to get a blue beam as an output when the red laser serves as your input, we must prevent the blue beam from being absorbed by that material which provides for the second harmonic generation. Therefore, its works best when that material is basically transparent. On the other hand, for electro optics applications, the input and output frequencies are the same. This allows one to deal with materials that have a much smaller band gap, especially if the input frequency is in the IR.

Sum over states expression for gamma

The expression for gamma can be simplified down to a three term model.

<math>\Gamma_{abcd} (-\omega_\sigma; \omega_1, \omega_2, \omega_3 ) = \hbar^{-3} K(-\omega_\sigma; \omega_1, \omega_2, \omega_3 ) x</math>

<math>\lbrace \rbrace</math>

<math>x \left \lbrace + \sum_p \left [ \sum_{m,n,p} \frac {<g|\mu_a|m>} {(\omega_{mg} -\omega_\sigma - i\Gamma_{mg})} \right ] \rbrace \,\!</math>