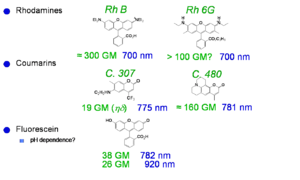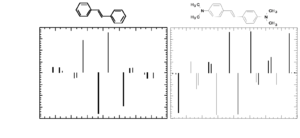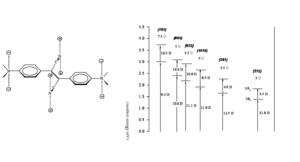Two Photon Absorption

Previous Topic

Return to Third-order Processes, Materials & Characterization Menu

Next Topic

Two-photon absorption (TPA) is a third order nonlinear optical phenomenon in which a molecule absorbs two photons at the same time. The transition energy for this process is equal to the sum of the energies of the two photons absorbed. The probability that a molecules undergoes two-photon absorption depends on the square of the intensity of the incident light, if the two photons are from the same beam (in the case of two incident beams, the transition probability depends on the product of the beams intensities). This intensity dependence is at the origin of the interest in two-photon absorbing materials for use in microscopy and microfabrication applications.

Two-Photon Excited Processes

Two-Photon Absorption

A molecule can be excited to state S₂ by absorption of two photons of energy hν_A.

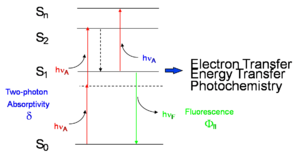
Two-photon absorption in a material can be quantified by the two-photon absorption cross section, a quantity that is proportional to the imaginary component of the χ⁽³⁾ tensor (or, on a molecular level, to the imaginary component of γ) and depend on the photon energy/energies. In the following we will discuss in detail the case of degenerate (or one-color) two-photon absorption, that is the case where the two photons have the same enrgy. The figure at right schematically illustrates the degenerate two-photon absorption process, in which two photons, each of energy hν_A, are simultaneously absorbed and the molecule is excited directly from the ground (S₀) state to an excited state (state S₂ in the figure) without the formation of an intermediate eigenstate. Neither of the two photons have enough energy to excite the molecule to S₂ by itself, but the sum of the energies of the two correspond to the energy of state S₂. The dotted line represents a virtual state (as opposed to an actual eigenstate of the system) that can be thought of as created by the absorption of the first photon and having a very short lifetime (on the order of 10^-15 sec if the photon energy is not in resonance with any electronic transition). If a second photon is absorbed within this lifetime, the two-photon absorption transition occurs and the molecule is excited to S₂.

Rate equations and selection rules for two-photon and one-photon absorption.

Once the molecule is in state S₂, it quickly relaxes by internal conversion to the lowest excited state (S₁ in the figure). From this state, the system can return to the ground state S₀ by emission of fluorescence or by nonradiative decay. Alternatively, an additional photon can be absorbed (bringing the molecule to a higher-lying excited state, S_n), or electron or energy transfer to another molecule can take place. Typically, once the molecule is in state S₁, the same set of processes will take place whether the molecule was initially excited into S₂ by two-photon absorption or directly into S₁ by one-photon absorption. For most known materials the two-photon absorption cross section, δ, is small and it is necessary to use intense laser beams in order observe the effects of two-photon absorption.

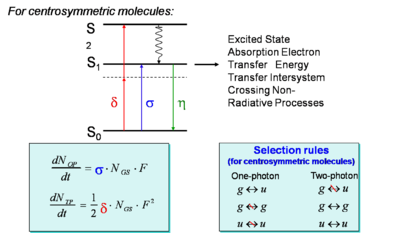
The rate equation that describes the formation of the excited state of a molecule by one-photon absorption can we written as follows:

<math>\frac {dN_{OP}} {dt} = \sigma N_{GS} F\,\!</math>

where

<math>\sigma\,\!</math> is the one-photon absorption cross section (and is related to the transition dipole moment of the molecule between the initial and final states of the transition)

<math>N_{GS}\,\!</math> is the number of molecules per unit volume in the ground state

<math>N_{OP}\,\!</math> is the number of molecules per unit volume in the excited state due to one-photon absorption

<math>F\,\!</math> is the photon flux (number of photons per unit area and time)

<math>t\,\!</math> is the time

(this is analogous to the equation to describe the rate of a reaction between two reactants, A and B, to give a product C: A + B = C, and that is first-order with respect to each of the reactants).

In a similar manner, the rate equation for two-photon absorption can be written as follows, keeping in mind that two photons are needed to produce one excited molecule (in the reaction analogy, the reaction is now second-order in the photon flux, but still first-order in the concentration of molecules):

<math>\frac {dN_{TP}} {dt} = \frac {1}{ 2} \delta N_{GS} F^2\,\!</math> is the rate for two photon absorption

where

<math>\delta\,\!</math> is the two-photon absorption cross section

<math>N_{TP}\,\!</math> is the number of molecules per unit volume in the excited state due to two-photon absorption

This shows that the probability of two-photon absorption depends on the square of the photon flux (or, equivalently, to the square of the light intensity). The selection rules for the two-photon absorption process are different from those for one-photon absorption (in analogy to the situation for infrared and Raman spectroscopies). In particular, a two-photon absorption transition is allowed only between two states that have the same parity. Thus, in molecules with an inversion center, transitions are two-photon allowed from a gerade (g) state to another gerade state or from an underage (u) to another ungerade state, but not between g and u states. In the case of one-photon absorption, instead, transitions are allowed between an initial state and final state with opposite parity (from g to u, or vice versa). This implies that, in centrosymmetric molecules, if the transition from the ground state to a given excited state is one-photon allowed it is not two-photon allowed and, vice versa, if it is two-photon allowed it is not one-photon allowed. For molecules without inversion center, certain transitions can be both one-photon and two-photon allowed. In the scheme above, the blue arrow represents the excitation of a centrosymmetric molecule to the lowest excited state, S₁, by the absorption of one photon (with one-photon absorption cross section σ); this transition is not two-photon allowed. The molecule can be excited by two-photon absorption (red arrows) into a higher-lying state, S₂ (with two-photon absorption cross section δ).

Advantages of TPA

Two photon absorption is considered to be a nuisance in the case of all-optical switching using χ⁽³⁾ materials because it causes attenuation of the light beam and damage to the material can result from severe heating of samples. However the two-photon absorption process can be exploited in another contexts, apart from being of interest in the study of fundamental spectroscopic properties of materials.

Two-Photon Processes Provide 3-D Resolution

Two laser beams are focused in a sample molecule in solution inside a cuvette; the top beam is tuned at a wavelength at which two-photon absorption can take place, the bottom one at a different wavelength that can excite the molecules by one-photon absorption. The blue light visible in the photograph is the fluorescence emitted by the molecules after excitation.

If a light beam is focused into sample at a wavelength suitable for one-photon absorption, molecules are excited throughout the beam path in the sample, as evidenced by the fluorescence emission in the bottom part of the cuvette at right. If the beam is tuned at a wavelength at which the material exhibits two-photon absorption, only the molecules located very close to the focus of the laser beam are excited (top beam in the photograph). This is related to the fact that the excitation rate depends on the square of the light intensity, as discussed above, and that in a focussed beam the light intensity is maximum at the focal plane and decreases approximately with the square of the distance from the focal plane, z, along the propagation direction (because the area of the beam increases moving away from the focus). Overall, the excitation rate for TPA and the intensity of the two-photon induced fluorescence decrease as the forth power of the distance from the focal plane. Consequently, in the solution in the figure the two-photon induced fluorescence is strongest at the beam focus and its intensity drops off very quickly on either side of the focal plane, resulting in what looks like emission from a "single point" (or small volume) in the solution. At the diffraction limit, the TPA excitation is confined to a volume on the order of the cube of the wavelength of the excitation light. Most of the applications of TPA are based on this ability to confine and control the excitation volume in a material with good resolution in three dimensions, as any excited state process that can take place in the material after two-photon excitation (such as fluorescence emission or energy transfer) will be confined to the same small volume.

TPA Processes Provide Improved Penetration of Light Into Absorbing Materials

One-photon absorption (bottom): a light beam from the right is quickly absorbed by a concentrated solution of a fluorescent material. Two-photon absorption (top) the beam is able to penetrate the solution without being attenuated until the focus of the beam; only near the focus the light intensity is high enough to activate two-photon induced fluorescence.

In the figure at right the same two beams as in the case above are focused in a solution of a fluorescent compound, but now the solution is much more concentrated. It can be seen that the for the bottom beam (one-photon absorption case) fluorescence emission can be seen only close to the right wall of the cuvette, as the beam is strongly absorbed and attenuated by the solution (the beam is propagating from right to left). Thus the penetration depth of the beam in the solution is small. In the case of the top beam, there is no one-photon absorption and two-photon absorption only occurs near the focus of the beam (in this case the center of the cuvette), so that there is no beam attenuation before the beam reaches the focus and the laser beam can penetrate farther into a sample with respect to the one-photon absorption situation. The ability to penetrate a material and to be focused accurately in three dimensions make the TPA process ideal for fluorescence imaging of thick samples (even in vivo) or in medical applications in which, for example, a drug can be activated by TPA at a very precise location without affecting the tissue above and below the focal plane of the excitation beam.

Measuring the two-photon absorption cross section

Schematic of an optical setup for a two-photon induced fluorescence experiment. The red line represents the excitation beam, the blue line is the two-photon induced fluorescence, the dashed line is a beam splitter and the solid black lines are filters (to control the beam intensity or to block the excitation beam before the PMT detectors).

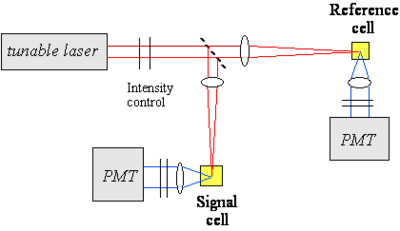
One of the techniques used to measure the TPA cross section of a material is based on two-photon induced fluorescence. In this measurement, a laser beam is propagated through the sample of interest (the beam can be focussed or collimated) and the fluorescence light that is emitted by the excited molecules after two-photon absorption is collected and measure by a detector (for example a photomultiplier tube, PMT). As seen above, the number number of molecules excited by two-photon absorption per unit time and volume, N_TP, is proportional to the TPA cross section of the material at that excitation wavelength, the concentration of molecules and the square of the photon flux. The number of fluorescence photon emitted by these molecules is then:

<math>n_{fl} = \eta N_{TP}\,\!</math>,

where η is the fluorescence quantum yield of the material.

Thus, the intensity of the two-photon induced fluorescence is proportional to the TPA cross section δ. This technique can be used for absolute or relative measurements of TPA cross sections. In the absolute case, all the relevant parameters (such as the instantaneous photon flux and the detection efficiency of the optical setup) need to be measured independently. In relative measurements, an unknown compound is analyzed under the same conditions as a material of known TPA cross section. The figure at right shows an example of optical setup that can be used for TPA cross section measurements. A tunable laser is needed to measure the TPA spectrum, as the TPA cross section depends on the excitation wavelength. In this example, the laser beam is split in two by a beam splitter and one of arm is used as reference for the intensity of the beam, to correct for fluctuations in intensity from pulse to pulse during the course of the measurement.

Measurement considerations:

• A pulsed laser is needed (pulse durations in the ns, ps, fs range can be used).

• The laser need to be tunable to obtain spectral information on the material.

• The two-photon fluorescence method is applicable to fluorescent materials (the z-scan technique can be used for fluorescent and non-fluorescent materials).

• The detection of the fluorescence emission can be done in various configurations (90º collection, backward scattering, forward scattering, ...); scattering of the excitation beam by the sample need to be removed from the fluorescence signal before detection (for example using filters or monochromators).

• The dependence of the two-photon induced fluorescence signal on the square of the laser beam intensity needs to be tested for the actual experimental conditions used, to exclude contributions from other effects.

• Possible reasons for deviation from the dependence on the square of the laser intensity: linear absorption, stimulated emission, ground state depletion, ...

• Importance of spatial and temporal profile of the excitation beam.

See equipment video on Two-Photon Spectroscopy

Calculation of TPA cross sections

Perturbative Expression for γ, as Relevent to Two-Photon Absorption

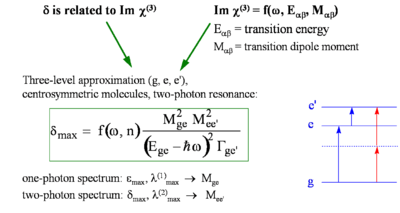
The perturbative expression for the hyperpolarizability γ for the frequency component relevant to for two-photon absorption can be written as follows (under the assumption that the system can be described by the so-called "three level model", in which only the ground state, g, the lowest excited state, e, and a higher-lying two-photon allowed state, e', are considered):

<math>\gamma( -\omega; \omega, -\omega, \omega) \propto \frac{ M^2_{ge} \Delta \mu^2_{ge}} {(E_{ge} - \hbar \omega - i \Gamma_{ge})^2(E_{ge}-2\hbar \omega -i \Gamma_{ge})} + \frac {M^2_{ge} M^2_{ee^{\prime}}} {(E_{ge} - \hbar \omega- i \Gamma_{ge})^2 (E_{ge^{\prime}} - 2 \hbar \omega - i\Gamma_{ge^{\prime}})}\,\!</math>

where:

<math>M_{ge} \,\!</math> is the transition dipole moment between states g and e

<math>M_{ge^{\prime}} \,\!</math> is the transition dipole moment between states g and e'

<math> \Delta \mu_{ge} \,\!</math> is the difference between the dipole moment of states g and e

<math>E_{ge} \,\!</math> and <math>E_{ge^{\prime}} \,\!</math> are the energies for the transitions between the subscripted states

<math> \omega \,\!</math> is the angular frequency of the excitation beam and

<math> \Gamma \,\!</math> are damping terms.

For a centrosymmetric molecule <math>\Delta \mu_{ge}\,\!</math> goes to zero (the dipole moment is zero in both g and e states) so that the first term in the equation for γ goes to zero. For non centrosymmetric molecules both terms contribute to the hyperpolarizability. From the equation above it can be seen that two-photon resonances can occur when the photon energy is such that: <math> 2 \hbar \omega = E_{ge} \,\!</math> or <math> 2 \hbar \omega = E_{ge^{\prime}} \,\!</math>

The TPA cross section (δ ) is proportional to the imaginary component of γ:

<math>\delta(\omega) = \frac {4\pi^2 \hbar \omega^2} {n^2c^2} L^4 Im \gamma( -\omega; \omega, -\omega, \omega)\,\!</math>

The above equation is valid in the cgs system of units; <math> n\,\!</math> is the refractive index of the material, <math> L\,\!</math> is the local field factor (which depends on the refractive index), and <math> c\,\!</math> is the speed of light.

Calculations of the TPA cross section in a donor-acceptor molecule

TPA calculations for stilbene

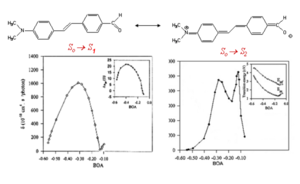
A simple donor/acceptor stilbene with an amino group and a formyl group on the phenyl rings in para position has been used a model compound for calculations of the TPA cross section. The figure at right shows the molecule in two resonance structures and the calculated TPA cross section as a function of the bond order alternation (BOA; i.e. the difference between the bond order in adjacent CC bonds in the vinylene bridge), which changes going from one resonance structure to the other. The value of δ for the transition from the ground to the first excited state (S₀ to S₁, left plot) is small for large negative values of the BOA (corresponding to the resonance structure on the left side), reaches a maximum when the BOA increases, and then it goes to zero when the BOA approaches the cyanine limit (BOA = 0). The same trend as a function of BOA is obtained for the change in dipole moments (see inset). The TPA cross section for the transition to the second excited state (S₀ to S₂, right plot) exhibits a more complicated behavior as a function of BOA and with multiple peaks are present, in part because of changes in the detuning term <math>E_{ge} - \hbar \omega\,\!</math>. When the energy for the transition to S₁ is very close to half of the energy for the transition to S₂, the detuning term becomes small and δ increase; this situation is referred to a "double resonance".

See T. Kogej et.al. Chem. Phys. Lett. 1998, vol. 298, p. 1

Examples of two-photon absorbing materials

Two-photon absorption spectrum of a centrosymmetric molecule

Two-photon and linear absorption spectra of the molecule shown (in toluene solutions).

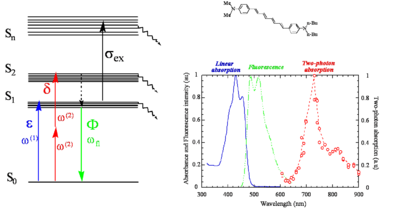
Here is a centrosymmetric molecule with a conjugated backbone and donor groups on both ends. The energy level diagram on the left side of the figure, similar to that discussed at the beginning of the section, shows the allowed transitions for this molecules. There can be one-photon excitation into S₁ (this transition is not two-photon allowed because the molecule is centrosymmetric) and two-photon excitation into S₂ (again for symmetry reason this transition is not one-photon allowed). After excitation, rapid relaxation can occur by internal conversion back to S₁ and then fluorescence emission from S₁. There is no fluorescence emission from S₂ because, in most cases, the relaxation from S₂ to S₁ is much faster than the fluorescence lifetime. In centrosymmetric molecules this can be easily understood, because the transition from S₂ to S₀ is symmetry forbidden for one photon, therefore the transition dipole moment for this transition is close to zero and the coupling between the grounds and the excited state is very small, resulting in a long radiative lifetime of the excited state. However even if the molecule was not centrosymmetric, the internal conversion relaxation from a higher-lying excited state is generally so fast that there still would not be fluorescence from S₂ (or S_n). This is known as "Kasha's rule", which was described by Michael Kasha and which states that, irrespective of the electronic state of the molecule reached by excitation, fluorescence will only occur from the lowest lying excited state (S₁). Most molecules behave according to Kasha's rule, but a few exceptions are know, such as azulene.

The figure also shows the one-photon (blue line) and two-photon absorption (red line) spectra of the molecule and the fluorescence emission spectrum (green line). In the graph note that the photon energy of the TPA band is lower (longer wavelength; the horizontal axis represent the wavelength of the excitation beam) than the one-photon absorption band (blue line) and of the fluorescence (green line). The TPA peak is around 720 nm, for this molecule. As two photons are involved in the transition, a TPA peak at 720 nm corresponds to a "transition wavelength" of 720 nm / 2 = 360 nm. The peak for linear absorption to S₁ is 430 nm. This shows that the state reached by two-photon absorption is higher in energy than the S₁ state and that there is very little one-photon absorption in this range (the small absorption seen at 360 nm is due to vibronic sub-levels of S₁), consistent with the selection rules described earlier for centrosymmetric molecules.

see Rumi et al., J. Am. Chem. Soc. 2000, vol. 122, p. 9500

Laser dyes

Xu and Webb measured the cross section for laser dyes a goupert mayer. One dye had cross section of 300 goupert meyer (two-photon absorptivity, δ, is expressed in Goppert-Mayer units (GM), with 1 GM=1×10^-50 cm⁴ s molecules⁻¹ photon⁻¹.). The process of two photon absorption was predicted by a German physicist Maria Goeppert Mayer in 1929. TPA was not actually observed until the early 60s when lasers were developed that had sufficient intensity to cause it. Most molecules have GM < 1. These dye have very high two photon cross sections..

See Xu and Webb Albota 1998 Fisher 1998

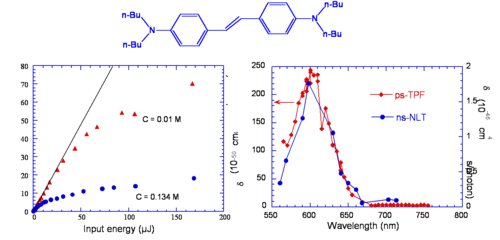
Vagaries of measurement: The “famous” AF-50

Various reported measurements of δ for AF-50

The chart shows various measurements for the molecule AF-50. This is indicative of the problems of measurement in the NLO field. The measurements were made using various techniques and conditions. The experiment with a delta of 11560 was conducted with a timescale of nanoseconds. This is duration is long enough for there to be a convolution of TPA and single photon absorptions that can appear to give a high TPA cross section. This high value could very well be useful for example in making coatings for safety glasses that could exclude high intensity laser light. But it is not useful for the scientific measurement of the molecules.

Optical Limiting via Two-Photon Absorption in bis-Donor Stilbene

Two photon fluoresence vs non linear transmission

This molecule behaves as an optical limiter. The curve of two photon fluoresence (TPF shown in red) and non linear transmission (NLT shown in blue) are similar except their scales are different. The NLT scale has units of 10^-46 and TPF is on the scale of 200, there is a factor of 100 difference. TPF is measure of the cross section, NLT is an effective cross section that involves two photon absorption followed by excited state absorption.

Initial Observations on Bis-Donor Stilbene

bis-Donor Stilbene

Bis Donor Stilbene (BDAS) is an instructive molecule to study.

Evidence for two-photon absorption

• The molecule is very electron rich
• Strong nonlinear transmission
• Strong blue fluorescence when pumped with orange light
• Fluorescence depends on I²
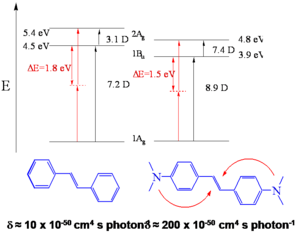
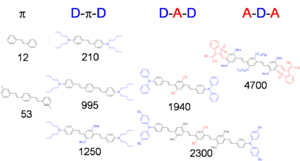
• Two-photon cross section, δ = 210 x 10^-50 cm⁴ s/photon, for stilbene δ = 12 x 10^-50 cm⁴ s/photon

The cross section is about 20 times that for the molecule without the electron donor groups. This is very high value and it is useful to learn why the donors have this effect.

Interesting features for two-photon applications

• High fluorescence quantum yield, φ_fl ~ 0.9
• High optical transmission
• Low oxidation potential, ED+/D = + 0.035 V vs. Fc/Fc+

It is very easy to oxidize in the ground state and is a powerful reducing agent in the excited state.

Proposed Model to Enhance TPA Cross Sections in Symmetrical Molecules

Theoretical calculations can help to explain this molecule’s properties.

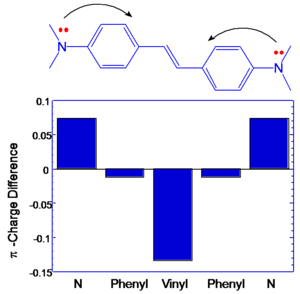
BDAS has large and symmetrical charge transfer from nitrogens (becoming more positive) to central vinyl group in the middle (becoming more negative) that is associated with large transition dipole moment between S₁ and S₂. (μ ee’² )

These results suggest that a large change in quadrupole moment between S₀ and S₁ is leads to enhanced delta. If you want to make dipole (or quadrapole) moment larger you can increase the distance over which charge is separated and you can increase the charge that is separated by that distance, or do both.

Bis Donor Substitution

This suggests certain design strategies for increasing the dipole or quandrupole moment. The transition dipole moment between the ground and first excited state is 7.2 for stilbene and 8.9 for BDAS. Between S₁ and S₂ the dipole goes from 3.1 D stilbene to 7.4 D for BDAS. This term is squared and this is the reason there such a high TPA cross section for BDAS.

<math>\delta_{S_0 \rightarrow S_2} \propto \frac {M^2_{ge} M^2_{ee^{\prime}}} {(E_1 - E_0 - \hbar \omega ) \eta} \,\!</math>

Transition Dipole Moments and BOA

If the components that contribute to transition dipole moments are located farther from the middle of the molecule there will be higher transition dipoles. In DBAS large coefficients on nitrogens coupled with extended distance from the molecular origin result in large excited state coupling.

Transition energy in eV for various conditions of charge transfer.

There is an optimal amount of charge transfer that is required to get the largest cross section.

Design of TPA chromophores

Chromophore variations and δ in 10^-50 cm⁴ s/photon

To get large quadrupole moment and large quadrupole moment changes you can do the following;

• Increase the distance between the donors so that you increase the distance over which you transfer the charge.
• Increase the strength of the donors so as to increase the amount of charge that is transferred.
• Add acceptors to the middle of molecule so that that section attracts charge.
• Flip the relation with donors in the center and acceptors on the end.

The diagram shows the effect on delta of different donors (shown in blue) and acceptors (shown in red) configurations and longer molecular chain lengths. The combination of these techniques achieves cross-sections in the thousands.

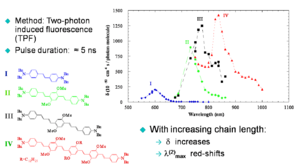
Chain-Length Dependence

Two Photon Fluorescence by wavelength for various length molecules

The graph shows that as the molecule gets longer the energy of the two photon absorption cross section decreases so the wavelength of the peak increases and the magnitude of the TPA increases due to the increasing transition dipole moments

Transition Dipole Moments

Here is an expression for delta that explores the change in transition dipole moment between the ground state and the excited state and the photon energy. The oscillator strength of the curve is calculated by integrating the absorption spectra plotted in energy and measuring the area under the curve. From this you can extract the transition dipole moment.

<math>\delta _{max} = f(\omega, n) \frac {M^2_{ge} M^2 _{ee^{\prime}}} {(E_{ge} - \hbar\omega)^2 \Tau_{ge^\prime}}\,\!</math>

where:

<math>\delta_{max}\,\!</math> is the cross sections that was measured.

<math>M_{\alpha\beta}\,\!</math> is the transition dipole moment for two levels α,β

<math>E_{\alpha\beta}\,\!</math> is the energy for absorption to for two levels α,β

<math>\hbar \omega\,\!</math> is the photon energy that was used to get the TPA.

<math>\Tau_ge^{\prime}\,\!</math> is the damping term which is estimated

In summary

<math>\delta_{ge} \propto M^2_{ge} M^2_{ee^\prime} , \Delta E^{-2}\,\!</math>

Effect of D/A Substitution

Trends for dipole moments of quadrupolar molecules

By making these molecules quadrupolar we increase the transition dipole moment between the first and second excited state (ee and ee’) The data supports this strategy.

Applications for TPA

Two-photon initiated polymerization and 3D microfabrication

TPA can be used to stimulate cross linking in a polymer.

Two photon absorption can be used to initiate polymerization on a precise microscopic scale. A beam can be focused at 3D coordinates in a polymer causing cross linking. Then non-crosslinked portions are washed away. This can be used for microfabrication. The model of the bull is about 5 microns wide and has some very fine features.

See Wu 1992

and Maruo 1997

"Micro bull"

"Thinking man"

Two-photon initiators with enhanced sensitivity

New dyes increase the effective range of power where 3D "writing" can occur, thus increasing the possible resolution

Regular photo-initiators are not excellent two photon absorbers. However a femptosecond layer can apply very large power. The goal is strike a power balance between the minimum writing range and the maximum destructive level. For conventional initiators there is only a factor of 2.5 in the power writing range. Newly developed two photon dyes expand this to range to a factor of 50. This lets you write more accurately and faster because the beam does not have remain in the same place as long.

Fluorescent and Refractive Bit Optical Data Storage

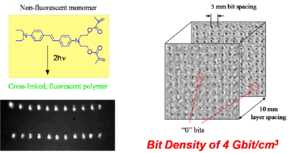
Fluorescent and Refractive Bit �Optical Data Storage

This technique can be used to convert non fluorescent polymer into a fluorescent form that has a higher density due to cross linking. If the density goes up and the polarizability stays the same the susceptibility goes up and the refractive index goes up. Peter Renzepus at the UC Urvine is using this method to create 3D optical memory. The ability to write on a 100 different planes increases the amount of information that can be stored (gigabits or terabits of data per cm³)

Photochemistry Generated via an Intramolecular Electron Transfer

Another method to initiate this process with electron transfer. A two photon dye connected to a photoactive group will absorb the two photons to cause photoinduced electron transfer (PET) producing a radical anion and radical cation. This group can cleave to give rise to photoproducts. There is a history of doing this kind of chemistry not necessarily with dyes connected to each other and not with two photon absorption.

Why 3D Micro and Nanofabrication

Examples of applications for nanofabrication

There is a technology pull towards miniaturization of devices and patterned materials.

• Need to free-form fabricate 3 dimensional structures
• Increasing need for ability to pattern a variety of materials
• Need to couple nano-scale object with micro-scale objects
• Areas impacted by 3D micro- and nano-fabrication include MEMs, microfluidics, photonics and tissue engineering. The photo on the left is a chain link fence is twice the thickness of a human hair. In tissue engineering cells grow better on certain topologies (ie scaffolds).

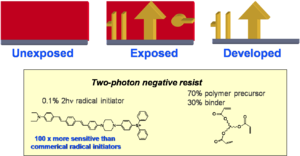
Media: Negative Tone Resist

Exposed areas remain after development in the positive tone resist process

This is an example of a two photon dye that creates a radical initiator. After absorption the radicals initiate polymerization. The polymer is less soluble and the nonpolymerized material thus this is a known as a negative photo resist.

Sub-diffraction limited resolution

TPA microfabrication of subdiffraction scale features. The lines are shown are 170nm.

Current lithography techniques are able to make structures at 60 nm. However TPA microfabrication can do this resolution with 3D resolution was well.

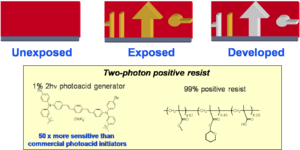
Media: Positive Tone Resist

In positive tone resist the exposed areas are removed during development

A positive tone resist becomes more soluble in portions that are exposed to light. This allows you to etch away material by exposing it with light.

Tetrahydropyran can be protonated on the oxygen creating a carbo cation thus converting the esther to a carboxylic acid. Esthers are not soluble in basic water but acids are so by dipping the material in an alkaline solution you can dissolve away the exposed material. A proton is needed.

A photo acid generator (PAG) will absorb light and then transfer an electron to the carbon sulfur sigma bond orbital, cause the bond to break homolytically yielding a methyl radical which will attack benzene and create a proton. The proton then starts the esther to acid reaction.

Micro-electromechanical Systems (MEMS) Applications

Micro electro mechanical systems are used for sensors, actuators, micromachines and optical switches. Inkjet heads and disc drive heads are MEMS. These can be fabricated with negative and positive tone materials.

MEMS image gallery

This example is drawn with a positive tone resist. The two pools are connected by a series of very fine tubes.

Microscopic Imaging

If you attach a two photon dye to a particular organelle and then scan the cell in 3D with a precise laser beam to build a detailed microscopic 3D model of the structure with submicron resolution. All of this technology begins with the design of molecules that are able absorb light effectively which goes back to third order nonlinear optics, polarizability and hyperpolarizability.

Summary

Perturbation theory predicts which molecules will have large two photon cross sections. Molecules with symmetrical quadrupolar charge transfer lead to large TPA cross sections because they have strong coupling between different excited states. Measurements need to be done very carefully using very short pulses and done over many wavelengths. There are many applications for TPA including microfabrication, optical limiting, and 3D microscopic imaging.