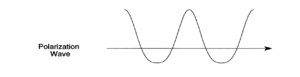Second-order Processes

Asymmetric Polarization

In second order non linear optics we are concerned with asymmetric polarization

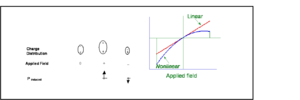
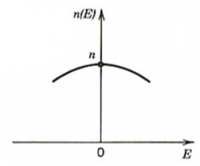
This is a representation of what happens to a molecules that is asymmetric when an electric field is applied. A molecule with a dipole such as 4-nitro aniline has a charge distribution that leads to a dipole. One side is a donor (d) and an acceptor (a) with a pi conjugated system. The magnitude of the induced dipole will be greatest when the electric field is aligned so as to move the electron density towards the electron donor end of the molecule. In a symmetric molecule is there a linear polarizability shown as the straight line. The greater the charge the greater the induced dipole. In an asymmetric material there an nonlinear effect which makes it easier to polarize in one direction than the other, and increasing field has an exponentially increasing effect.

In the presence of an oscillating electric field a linear material will have an induced dipole that is in phase and has the same frequency as the applied field.

An asymmetric polarization response to a symmetric oscillating field

The application of a symmetric field (i.e. the electric field associated with the light wave) to the electrons in an anharmonic potential leads to an asymmetric polarization response. This polarization wave has flatted troughs (diminished maxima) in one direction and sharper and higher peaks (accentuated maxima) in the opposite direction, with respect to a normal sine wave.

It is possible to go back and find the sum of waves that would result in such a wave (fourier transform). In the case of a symmetric polarization it is simply the sine wave of the applied field.

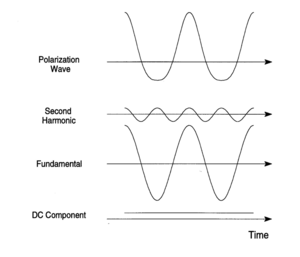
This asymmetric polarization can be Fourier decomposed (deconvoluted) into a static DC polarization component and components at the fundamental frequency superimposed with a second harmonic frequencies (at twice the fundamental frequency). This is a consequence of the material having second order non-linear properties.

As a consequence if you shine a laser at a non-linear optical material you can get light out of a different wavelength than the exciting source. In addition this emission can occur at a wavelength where the molecule is completely non-absorbing. This emission is not due to absorption / fluoresence. In second harmonic generation the light coming out can be twice frequency of the exciting source and the phenomena is tunable.

A laser of one frequency can be used to generate light of other frequencies. For example green light from a niodinum YAG laser (1064nm wavelength - green) can be directed on a non-linear optical crystal such as potassium dihydrogen phosphate and generate a second harmonic which is then used as a source for other experiments.

Since only the time averaged asymmetrically induced polarization leads to second-order NLO effects, only molecules and materials lacking a center of symmetry possess them.

Fourier Analysis of Asymmetric Polarization Wave

This asymmetric polarization can be Fourier decomposed (deconvoluted) into a static DC polarization component and components at the fundamental frequency superimposed with a second harmonic frequencies (at twice the fundamental frequency). This is a consequence of the material having second order non-linear properties.

As a consequence if you shine a laser at a non-linear optical material you can get light out of a different wavelength than the exciting source. In addition this emission can occur at a wavelength where the molecule is completely non-absorbing. This emission is not due to absorption / fluoresence. In second harmonic generation the light coming out can be twice frequency of the exciting source and the phenomena is tunable.

A laser of one frequency can be used to generate light of other frequencies. For example green light from a niodinum YAG laser (1064nm wavelength - green) can be directed on a non-linear optical crystal such as potassium dihydrogen phosphate and generate a second harmonic which is then used as a source for other experiments.

Since only the time averaged asymmetrically induced polarization leads to second-order NLO effects, only molecules and materials lacking a center of symmetry possess them.

Expression for Microscopic Nonlinear Polarizabilities

The linear polarizability is the first derivative of the dipole moment with respect to electric field. In non-linear optical effects the plot of induced polarization vs applied field can be corrected using higher corrections with a Taylor series expansion, including the second derivative of the dipole moment with respect of field times the field squared with a single electric field, or higher order terms using the third derivative of dipole moment vs field the field cubed. Mu is the total dipole moment in the molecule which is a sum of the static dipole plus several field dependent term.

<math>\mu = \mu_0 + (\partial \mu_i / \partial E_j)_{E_0}E_j + 1/2 (\partial^2 \mu_i / \partial E_jE_k)_{E_0} E_jE_k+ 1/6(\partial^3\mu_i / \partial E_jE_kE_j)_{E_0} E_jE_kE_j\,\!</math>

Where

<math>\mu\,\!</math> is the microscopic nonlinear polarizability

<math>E_i E_k E_j\,\!</math> are the electric field (vectors)

<math>\mu = \mu_0 + \alpha_{ij}E_j + \beta _{ijk}/ 2 E e + \gamma_{ijkl} / 6 E E E + ...\,\!</math>

where:

<math>\Alpha\,\!</math> is linear polarizability

<math>\Beta\,\!</math> is the first hyperpolarizability ( a third rank tensor with 27 permutations although some are degenerate)

<math>\gamma\,\!</math> is the second hyperpolarizability, responsible for third order non linear optics.

The terms beyond αE are not linear (they have exponential terms) in E and are therefore referred to as the nonlinear polarization and give rise to nonlinear optical effects. Note that Ej, Ek, and Ej are vectors representing the direction of the polarization of the applied field with respect to the molecular coordinate frame. Molecules are asymmetric have different polarizabilities depending the direction of the applied electric field.

Alpha is the second derivative of the dipole moment with respect to field is also the first derivative of the polarizability with respect to field. Beta is the first derivative of polarizability with respect to field, and gamma is the first derivative of the first hyperpolarizability with respect to field.

Nonlinear polarization becomes more important with increasing field strength, since it scales with higher powers of the field (quadratic or cubic relationships). Second harmonic generation was not observed until 1961 after the advent of the laser. Under normal conditions,

<math>\alpha_{ij}E > \beta_{ijk}/2 E·E > \gamma_{ijkl} /6 E·E·E.\,\!</math>

Thus, there were few observations of NLO effects with normal light before the invention of the laser with its associated large electric fields.

With very large electric fields there can be dielectric breakdown of the material.

The observed bulk polarization density is given by an expression analogous to (7):

<math>P = P_o + \chi^{(1)} ·E + \chi^{(2)}·· EE + \chi^{(3)}···EEE+ ...\,\!</math> (8)

where the :<math>\chi^{(i)}\,\!</math> susceptibility coefficients are tensors of order i+1 (e.g.,  :<math>\chi^{(2)}_{ijk}\,\!</math>). Po is the intrinsic static dipole moment density of the sample.

The linear polarizability is the ability to polarize a molecule, the linear susceptibility is bulk polarization density in a materials which has to do with the polarizability of the molecules and the density of those molecules in the material. More molecules means a higher susceptibility.

Taylor Expansion for Bulk Polarization

Consider a simple molecule with all the fields being identical.

<math>P = P_o + \chi^{(1)} ·E + 1/2\chi^{(2)}·· E^2 + 1/6\chi^{(3)}···E^3+ ...\,\!</math>

In a Taylors series expansion the dots refer the fact that these are tensor products. Just as a molecule can only have a non-zero beta if it is noncentrosymmetric, a material can only have a :<math>\chi^{(2)}\,\!</math> if the material is noncentrosymmetric (i.e., a centrosymmetry arrangement of noncentrosymmetric molecules lead to zero :<math>\chi^{(2)}\,\!</math>) .

In a centrosymmetric material a perturbation by an electric field (E) leads to a polarization P. Therefore, application of an electric field (–E) must lead to a polarization –P.

Now consider the second order polarization in a centrosymmetric material.

<math>P = \chi^{(2)}·· E^2,\,\!</math> (10)

<math> –P = \chi^{(2)}·· (–E)^2 = \chi^{(2)}·· E^2\,\!</math> (11)

which can only occur when P = 0, therefore :<math>\chi^{(2)}\,\!</math> must be 0.

This means that if we use quantum mechanics to design molecules that will have large hyperpolarizabilities the effort will be wasted if the molecules arrange themselves in a centrosymmetric manner resulting in bulk susceptibility of zero. The design therefore must include both arranging for the desired electronic properties, but also configuring the molecule so that those molecules will not line up in a centrosymmetric manner in the material. A solution of molecules can also exhibit some centrosymmetry.

Frequency Doubling and Sum-Frequency Generation

One nonlinear optical phenomena is that when you shine light at one frequency on a material you get out light with twice the frequency. This process is known as sum or difference frequency mixing. Two beams with frequency ω 1 and ω 2 when summed you get a sum of 2 x ω or, if ω1 – ω 2 results in a zero frequency electric field, which is a simple voltage.

The electronic charge displacement (polarization) induced by an oscillating electric field (e.g., light) can be viewed as a classical oscillating dipole that itself emits radiation at the oscillation frequency.

For linear first-order polarization, the radiation has the same frequency as the incident light.

Taylor Expansion with Oscillating Electric Fields-SHG

The electric field of a plane light wave can be expressed as

<math>E = E_0 cos(\omega t)\,\!</math>

Using a power series expansion :<math>Ecos^2(\omega t) E\,\!</math> can be substituted for E

<math>P = (P_0 + \chi^(1)E_0cos(\omega t) + \chi^{(2)} E_0^2cos^2(\omega t) + \chi^{(3)} E0^3cos^3(\omega t) + ...\,\!</math>

Where

<math>P_0\,\!</math> is the static polarizablity

Since :<math>cos^2(\omega t)\,\!</math> equals :<math>1/2 + 1/2 cos(2 \omega t)\,\!</math>, the first three terms of equation (13) become:

<math>P = (P^0 + 1/2\chi^{(2)} E_0^2) + \chi^{(1)}E_0cos(\omega t) + 1/2 \chi^{(2)}E_0^2cos(2 \omega t) + ..\,\!</math> (14)

This is the origin of the process of optical rectification and second harmonic generation.

Second Harmonic Generation (SHG)

<math>P = (P^0 + 1/2\chi^{(2)} E_0^2) + \chi^{(1)}E_0cos(\omega t) + 1/2 \chi^{(2)}E_0^2cos(2 \omega t) + ..\,\!</math> (16)

Physically, equation (16) states that the polarization consists of a:

Second-order DC field contribution to the static polarization (first term),

Frequency component w corresponding to the light at the incident frequency (second term) and

A new frequency doubled component, :<math>2\omega\,\!</math> (third term)-- recall the asymmetric polarization wave and its Fourier analysis.

Sum and Difference Frequency Generation

In the more general case (in which the two fields are not constrained to be equal), NLO effects involves the interaction of NLO material with two distinct waves with electric fields E1 with the electrons of the NLO material.

Consider two laser beams E1 and E2, the second-order term of equation (4) becomes:

<math>\chi^{(2)}·E_1cos(\omega_1t)E_2cos(\omega_2t)\,\!</math> (15)

From trigonometry we know that equation (15) is equivalent to:

<math>1/2\chi^{(2)}·E_1E_2cos [(\omega_1 + \omega_2)t] +1/2\chi^{(2)}·E_1E_2cos [(\omega_1 - \omega_2)t]\,\!</math> (16)

Thus when two light beams of frequencies w1 and w2 interact in an NLO material, polarization occurs at sum :<math>(\omega_1 + \omega_2)\,\!</math> and difference :<math>(\omega_1 - \omega_2)\,\!</math> frequencies.

This electronic polarization will therefore, re-emit radiation at these frequencies.

The combination of frequencies is called sum (or difference) frequency generation (SFG) of which SHG is a special case. This is how a tunable laser works.

Note that a very short laser pulse will result in a band or distribution of frequencies due to the Heisenberg Uncertainty Principle. Those bands will add and subtract resulting in some light which is twice the frequency if they added and some light that is very low frequency (0+ or – the difference), resulting from the difference between the frequencies. This is the process enabling Terahertz spectroscopy. Terahertz is very low frequency light.

Low frequency light is scattered less than high frequency light. For example if you look through a glass of milk there is “index inhomogeniety” in the milk due the presence of protein and fat. Terahertz radiation can be used for surveillance. A terahertz detector scanner will reveal materials that have different index of refraction.

Electro-optic effects

John Kerr and Friedrich Pockels discovered in 1875 and 1893, respectively, that the refractive index of a material could be changed by applying a dc or low frequency electric field. This are in fact non-linear optical effects but they often not thought of as such because they don’t require a laser.

Electric impermeability of a material can be expressed as:

<math>n \equiv \frac {\epsilon_0}{\epsilon} = \frac{1}{n^2}\,\!</math>

<math>\eta (E) = \eta + rE +SE^2\,\!</math>

Where

<math>\epsilon_0\,\!</math> is the dielectric constant of free space

<math>\epsilon\,\!</math> is the dielectric constant

Pockels effect

The Pockels effect has a linear relation to applied field

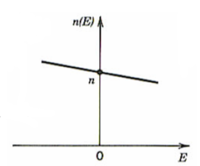
In the Pockels effect an applied electric field changes the refractive index of certain materials.

<math>\eta(E) = n – \frac {1} ²rn^3 E\,\!</math>

Where:

r is Pockels coefficient or Linear electro optic coefficient, r~ 10-12 – 1—10 m/V, typically

This is a linear function with respect to the electric field, the higher the r the greater the change. It is cubic with respect to the refractive index so materials with high intrinsic refractive indexes will change more. Some examples include NH₄H₂PO₄(ADP), KH₂PO₄(KDP), LiNbO₃, LiTaO₃, CdTe
The Kerr effect

The Kerr effect has a parabolic relationship to applied field

<math>\eta(E) = \eta – ½ Sn^3E^2\,\!</math>

Where

S is the Kerr coefficient

• S~ 10-18 – 10-14 mV in crystals
• S~ 10-22 – 10-19 mV in liquids

This is similar to the Pockels effect except that the refractive index varies parabolically or quadratically with the electric field.

This a process that occurs in second order nonlinear optical materials. It is a third order nonlinear optical process. Not all materials are second order nonlinear optical materials, only those that are centrosymmetric. However all materials have a :<math>chi^{(3)}\,\!</math> even if they are centrosymmetric.

It is possible to change the amplitude, phase or path of light at a given frequency by using a static DC electric field to polarize the material and modify the refractive indices. When light enters a material with a higher refractive index it is phase shifted and the waves become compressed. The direction is also changed. So by changing the refractive index it is possible to change the path of the light.

Consider the special case :<math>\omega_2 = 0\,\!</math> [equation (15)] in which a DC electric field is applied to the material.

The optical frequency polarization (P_opt) arising from the second-order susceptibility is:

<math>\chi^{(2)}·E_1E_2(cos \omega_1 t)\,\!</math> (17)

where E1 E2 is the magnitude of the electric field caused by voltage applied to the nonlinear material (a voltage not optical frequency).

Recall that the refractive index is related to the linear susceptibility that is given by the second term of Equation (14):

<math>\chi^{(1)}·E_1(cos \omega_1 t)\,\!</math> (18)

so the total optical frequency polarization (Popt) is the chi1 term plus the chi2 term:

<math>P_{opt} = \chi^{(1)}·E_1(cos_1t) +\chi^{(2)}·E_1E_2(cos \omega_1t)\,\!</math> (19)

Then factor out  :<math>E_1(cos \omega_1t)\,\!</math>

<math> P_opt = [\chi^{(1)} + \chi^{(2)}·E_2] E_1(cos \omega_1t)\,\!</math> (20)

Chi1 is linear susceptability which relates to the dielectric constant, which in turn relates to the square of the refractive index. A change in the linear susceptablity changes the index of refraction. The second term: χ² times the magnitude of the voltage (E₂) means that the susceptability of the material, the dielectric constant of the material, and the refractive index of the material can be altered by changing the applied voltage.

You can shine light on second order nonlinear optical materials and get out different frequencies, or shine one laser beam, apply an electric field and then modulate the refractive index. For example, light can travel freely between two fibers that are very close to each other with the same refractive index. But if the fibers have a different refractive index light will stay in one fiber or the other.

By changing the refractive index you can move light from one fiber to another; it provides a means of switching light in waveguides.

Summary

• The applied field in effect changes the linear susceptibility and thus the refractive index of the material.

• This is, known as the linear electro-optic (LEO) or Pockels effect, and is used to modulate light by changing the applied voltage.

• At the atomic level, the applied voltage is anisotropically distorting the electron density within the material. Thus, application of a voltage to the material causes the optical beam to "see" a different material with a different polarizability and a different anisotropy of the polarizability than in the absence of the voltage.

• Since the anisotropy is changed upon application of an electric field, a beam of light can have its polarization state (i.e., ellipticity) changed by an amount related to the strength and orientation of the applied voltage, and travel at a different speed and possibly in a different direction.

Index modulation

Quantitatively, the change in the refractive index as a function of the applied electric field is approximated by the general expression:

:<math>1/n_{ij}2 = 1/n_{ij}2 + r_{ijk}E_k + s_{ijkl}E_kE_l + ... \,\!</math> (21)

where

<math>n_ij\,\!</math> are the induced refractive indices,

nij is the refractive index in the absence of the electric field,

<math>r_ijk\,\!</math> is the linear or Pockels coefficients, Δn for E = 10⁶ V/m is 10^-6 to 10^-4 (crystals) and;

<math>s_{ijkl}\,\!</math> are the quadratic or Kerr coefficients.

r coefficients

The optical indicatrix (that characterizes the anisotropy of the refractive index) therefore changes as the electric field within the sample changes. If you map the index of refraction with respect to each polarization of light you end up with a surface that looks something like a football. The electric field allows you to change the shape of the football.

Electro-optic coefficients are frequently defined in terms of r_ijk. The "r" coefficients form a tensor (just as do the coefficient of alpha).

The subscripts ijk are the same as those used with beta. The first subscript (i) refers to the resultant polarization of the material along a defined axis and the following subscripts J and K refer to the orientations of the applied fields, one is the optical frequency field and k is the voltage.

Technological Applications Of The Pockels Effect

A Mach Zehnder Interferometer converts an input light beam into a modulated beam

The Pockels effect has many important technological applications.

Light traveling through an electrooptic material can be phase of polarization modulated by refractive index changes induced by an applied electric field.

Devices exploiting this effect include optical switches, modulators, and wavelength filters.

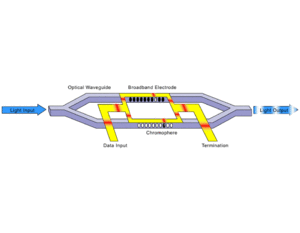
The Mach Zehnder interferometer is a device that uses differences in index of refraction to switch light. Two beams of light can be split into paths, traverse the same distance and the recombine them. If the two beams encounter identical paths there will be constructive interference (call it 1). If one of paths is changed so that there is a 180 degree phase shift (π phase shift) the two beams will recombine with destructive interference ( call it 0). By applying an electric field to a second order nonlinear optical material the index of refraction is changed and the phase of light is changed with respect to the first beam. Thus light can be turned on and off using an electrical field. This is the essence of digital telecommunication modulation.

The timescale for electronic polarization is femptoseconds (vibrational polarization requires picoseconds). This fast switching increases the bandwidth (bits per second) possible for optical communication. Today people are happy with 40 gigabits per second but his wont last for long. Lithium niobate will eventually run out of speed from a purely physical standpoint. Electronic polarization of organic materials hold the promise of greatly increasing speed.

The EO effect can be used to transduce electrical signals into optical signals. Electrical information appears as an amplitude modulation on the optical transmission. The modulator works for analog or digital data. Vpi is the voltage that is required to get a pi phase shift.

<math>V\pi = \lambda d/ ( 2 n^3 r_{33} L \Gamma)\,\!</math>

Where:

<math>\Lambda\,\!</math> is the optical wavelength

<math>N\,\!</math> = index of refraction

<math>R_{33}\,\!</math> is the electro-optic coefficient

<math>L\,\!</math> = the interaction length

<math>\Gamma\,\!</math> = modal overlap integral

<math>D\,\!</math>= electrode gap

It is desirable to have a low drive voltage because there is dissipation of power creating heat which is a problem when you have many modulators in a small space. In order to keep the V_π low try to use materials that have a high r₃₃ and a high refractive index. You will be able to use knowledge of donors and acceptors, and the structure of molecules to first optimize the molecules and then the materials for electro optical activity.

Applications of Electro-optic Devices

EO materials can be used at many locations in a network

A network has a variety of devices that provide input from to a transmitter, connected by a electro-optic modulator (EOM) through a switching network, to a receiver with a photodetector, and then are connected to display devices. Nonlinear optical materials can be used for any of these application. They can used to create terahertz radiation and to create specific wavelengths of light for spectroscopy.

Poled Polymers

Assume you are start with molecules that have high nonlinearities but they are arranged in a random orientation.

In the poled polymer concept, one attempts to noncentrosymmetrically incorporate a high number density of NLO active molecules.

An NLO chromophore with a dipole moment (such as paranitroaniline) and a glassy polymer are dissolved in an organic solvent and spin-coated onto a substrate. The film is then heated above or around its glass transition temperature. The glass transition temperature at which there is free motion of the main chain of the polymer.

At this temperature, the molecules can rotate in the rubbery matrix. An intense DC electric field as high as 106 V/cm is applied and this field creates a force on the dipole moments of the chromophores, aligning them.

Thus, the polymers and chromophores must be nonconducting to support these large fields. With the electric field still applied, the film is cooled below the Tg of the polymer, restricting the motions of the chromophores.

In this manner you can produce a material that has a second order nonlinear optical effect using molecules that have a second order nonlinear optical effect.

The resulting noncentrosymmetric structure contains the molecular units oriented on the average normal to the film (C∞v symmetry). In this state, the electric field of an optical beam propagating through the film can be maximally modified when the field is parallel to the orientated molecular units.

Using a non-interacting oriented molecular gas model, the follow equation has been derived to describe the second-order susceptibility in the direction of the poling field (:<math>\chi^{(2)}_333\,\!</math>).

<math>\chi^{(2)}_{333} = N F\Beta_{/mu}<cos^3\theta>\,\!</math>

where :<math><cos^3\theta> = \mu_z E_p/ckT\,\!</math>

N is the number density of chromophores in the material, k is the Boltzman constant, T is the temp in Kelvin and

c is a system-dependent factor equal to 5 for isotropic systems, and 1 for ideal liquid crystalline systems (Ising systems).

The term :<math><cos^3\theta>\,\!</math> is the induced polar order which is an average angular orientation where :<math>\theta\,\!</math> is the angle between the poling axis and the molecular dipole moment of the chromophores.

The brackets indicate the Boltzman thermal average. This equation is valid at low field, :<math>\mu_zEp<kT\,\!</math>.