Photochromism

Previous Topic

Return to Absorption and Emission Menu

Next Topic

Definition

Photochromism is a reversible transformation of a chemical species induced in one or both directions by absorption of electromagnetic radiation between two forms, A and B, having different absorption spectra. A common example is the sunglasses that turn dark when exposed to sunlight. In order to qualify as photochromic the different forms of the species must have different absorption spectra.

Good References Photochromism by Brown

Photochromism, Molecules, and Systems by Dürr

Photochromism is derived from the Greek words: phos (light) and chroma (color). When light of wavelength lambda1 is exposed to species A it goes to B and when B is exposed to light with wavelength lambda 2 or in the presence of heat, B goes to A.

<math>A \Leftrightarrow^{\lambda_1}_{\lambda_2, \Delta}B\,\!</math>

Species A gives rise to species B with a different absorption spectrum.

The example spectra of A absorbs around 350 nm and B absorbs around 500nm. One of the ways that you can control the transition is by changing the wavelength of the absorbing light, if they have different spectra. Photochromic materials are used in optical memory in which case you want A to go B and stay there. In this case it desirable that the heat driven transition from B back to A be very small.

The first report of photochromism was given by Fritzsche 1867 who observed the bleaching of an orange-colored solution of tetracene in the daylight and the regeneration of the color in the dark.

Tetracene is a four ring conjugated colored molecule. When the crystals are exposed to sunlight the molecule is broken into the two smaller molecules neither of which absorbs in the visible also known as bleaching. There is transient bleaching, permanent or semi transient types of bleaching.

Interconversion of Isomers

A photochromic conversion of A to B, and B to A can be described by the equations:

<math>

N_{A\rightarrow B} = N_A .f(\epsilon^A(\lambda), I(\lambda)). \phi_{A \rightarrow B}\,\!</math>

<math>N_{B\rightarrow A} = N_A .f(\epsilon^B(\lambda), I(\lambda)). \phi_{B \rightarrow A}+ N_B .f’(T)\,\!</math>

Where:

<math>f(\epsilon^X(\lambda), I(\lambda))\,\!</math> is the fraction of molecules of the species x that is excited by the light per unit time,

<math>f(\epsilon^X(\lambda), I(\lambda))\,\!</math> is a function of the extinction coefficient of the molecule :<math>[\epsilon^X(\lambda)]\,\!</math> at wavelength l and of the light intensity :<math>[I(\lambda)]\,\!</math> at that wavelength (the absorption spectra)

<math>\phi_{A\rightarrow B}\,\!</math> is the quantum yield the conversion of A to B

<math>\phi_{B\rightarrow A}\,\!</math> is the quantum yield of the conversion of B to A

<math>f'(T)\,\!</math> is the fraction of molecules B that thermally convert to A per unit time, it is a function of temperature [T] (thermal reversal)

The rate of absorption is the rate that molecules go from the ground to the excited state because of the collision with a photon. The rate law for this chemical reaction would be dependent on the concentration of A and the rate of photo flux and the probability of a photo being absorbed. In order for A to go to B it must achieve an excited state. The quantum yield predicts how often the excited state will lead to the formation of B as opposed to decaying, giving off a photo or other non-productive outcomes.

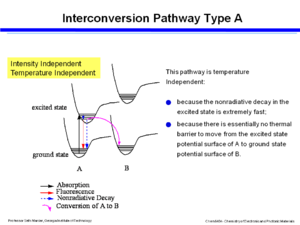
Interconversion – poor coupling

Consider the exited state and ground state potential surfaces. If you assume that the excited state potential well between A and B are not strongly coupled or do not interact then the photon is absorbed into the excited state, over a period of 100s of femptoseconds the molecule relaxes down to the lower vibrational levels within the excited state, and then it can go back down buy fluoresence or non-radiative decay. If the excited state of A goes directly to the ground state of B that will be a temperature independent process because it is extremely fast and because the excited state can slide easily back to the ground state of A because there is no thermal barrier. This pathway is intensity dependent.

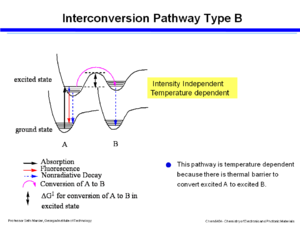
Interconversion- strong coupling

If there is strong coupling of the two potential wells in the excited state of the two species then energy moves by a thermally activated process in the excited states. You are not forming the ground state of B directly, instead you are forming an excited state of B which then goes to the ground state by fluorescence or non-radiative decay. This pathway is temperature dependent because there is thermal barrier to convert excited A to excited B. You can control the outcome of reaction and its equilibrium by changing the temperature. However it is not dependent on intensity.

Photostationary State

A photostationary state occurs when under irradiation the rate of A &rarr B equals the rate of B &rarr A at dynamic equilibrium. This is dynamic because we are not a thermal equilibrium, we are continually adding photons. The details of the photons makes a big difference. Suppose you have a molecule A that absorbs at exactly 400nm and its counterpart B absorbs at 500nm. If you excite this molecule at 400nm and there is some quantum yield of A going to B and there little thermal conversion from B to A then the photostationary state will be 100% B. You are exciting A it goes to B but it has no way of getting back. If you excite at 500nm the the photostationary state will be 100% A. The distinction between the equilibrium and the photostationary state is that the latter depends on the wavelength of the light source, the overlap with the absorption spectra of the two molecules and the quantum yields for each of the reactions. It is the number of number of A or B over the total number of molecules.

The photostationary composition is defined as:

NAorB/(NA+NB) at dynamic equilibrium

Here, NA-->B= NB-->A

Thus:

NA .f(eA(l), I(l)). fA-->B = NB .f(eB(l), I(l)). fB-->A+ NB .f’(T)

The rate is determined by number of molecules, the overlap of extinction coefficient and the intensity of the light at each wavelength and the quantum yield. Light sources rarely have equal intensities over all wavelengths. When the two parts of the equation are equal there is photostationary state.

Isosbestic Point

Consider the absorption spectra of a composite comprised of A and B. The absorption at lambda equals the number of molecules of A times the extinction coefficient of A at lambda plust the number of molecules of B plus the extinction coefficient of B at lambda.

At any wavelength the absorption at a given wavelength, A(l), of a two-component system (photochromism is a special case) is given by:

A(l)= NAeAl + NBeBl

If at one wavelength the extinction coefficients are equal they can be factored out:

  

Then that wavelength definesthe isosbestic point because:

A(l)= el (NA + NB)= el Ntot

The isobestic point is the point where the absorption remains constant.

References

Previous Topic

Return to Absorption and Emission Menu

Next Topic