Sigma and pi Orbitals
Return to Molecular Orbitals Menu | Next Topic
Molecular Orbital Theory
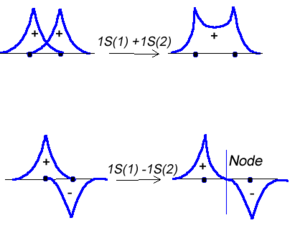
Molecular orbital theory was developed in the early part of the last century to help rationalize why bonds form and to explaint the properties of molecules. In molecular orbital theory the atomic orbitals from each atom can overlap with those on other atoms. Since the atomic orbitals are wavefunctions and behave like waves it is possible for them to overlap in a constructive manner to form a bonding orbital.
<math>\Psi_{new} = \Psi_1 + \Psi_2\,\!</math>
Or the two functions can combine in a destructive manner.
<math>\Psi_{new} = \Psi_1 - \Psi_2\,\!</math>
This is sometimes referred to as Linear Combination of Atomic Orbitals (LCAO). When there is a destructive combination of the two wave results in a node between the two atoms where the there is a zero probability of finding the electron. The first case is known as a bonding orbital and the bottom case is known as an anti-bonding orbital.
Note theat the electron density is higher between the nuclei in the bonding molecular orbital and the that the orbital is stabilized, that is lower in energy relative to the two isolated hydrogren atoms. The sign of both wavefunctions is positive. There is a decreased electron density between the atoms in the antibonding molecular orbital and the orbital is destabilized, that is higher in energy, than the two isolated hydrogen atoms. In very simple molecular orbital theory we treat the destabilization energy of the antibonding orbital as identical to the stabilization energy of the bonding orbital but in fact it is slightly more destabilized than the bond orbital is stabilized.
Orbital Overlap
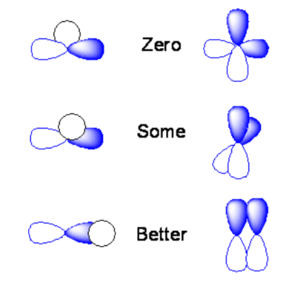
The amount of stabilization or destabilization is referred to a their orbital overlap. Mathematically the overlap is an integral of from negative infinity to positive infinity of a product of two wavefunctions over all space.
<math>\int_{-\infty}^{\infty} \Psi_1^* \Psi_2\,\!</math> = Overlap
The area under the curve for these functions is the orbital overlap. If the s orbital is lined up exactly over the node of a p orbital you will end up with positive overlap on one side, and equal and opposite overlap on the other side. The orbital overlap when you integrate over all space will be identically zero. If you take two p orbitals that are oriented at 90 degrees the product is zero. If you shift the s orbital a little bit one direction the overlap of the s orbital with one of the lobes will be non-zero. If you have two p orbitals at some angle you will have non-zero overlap. Or if a s orbital overlaps only on side of a the p orbital you would get some orbital overlap. The two p orbitals that are aligned with the same sign will have the maxiumum bonding overlap. If they are arranged with opposite signs you have the maximum antibonding condition.