Difference between revisions of "Marcus Theory and Reorganization Energy"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| Line 136: | Line 136: | ||
In order to determine if a molecule will have favorable transport properties in a device you would like to know how mobility changes going from low to high temperature when the material in a thin film or crystalline form. Marcus theory does allow you to do that. The electronic couple is derived for a single crystal structure but the Marcus equation doesn’t consider modifications in electronic coupling that occur with increasing temperature. The intermolecular component of reorganization energy (λ <sub>s</sub>)(s stands for surrounding) is treated in a purely classical way in Marcus theory. | In order to determine if a molecule will have favorable transport properties in a device you would like to know how mobility changes going from low to high temperature when the material in a thin film or crystalline form. Marcus theory does allow you to do that. The electronic couple is derived for a single crystal structure but the Marcus equation doesn’t consider modifications in electronic coupling that occur with increasing temperature. The intermolecular component of reorganization energy (λ <sub>s</sub>)(s stands for surrounding) is treated in a purely classical way in Marcus theory. | ||
:<math>k_{ET} = ( \frac {4 \pi^2} { h}) t^2 \left(\frac {1} {4\pi \lambda_s kT}\right)^{1/2} \sum_\upsilon \prime exp(-S) \frac {S^{\upsilon\prime}} {\upsilon \prime !} exp \left(-\frac {(\Delta G^0 + \lambda_s + \upsilon\prime \hbar \langle \omega_v \rangle)^2} {4\lambda_s kT} \right)\,\!</math> | :<math>k_{ET} = ( \frac {4 \pi^2} { h}) t^2 \left(\frac {1} {4\pi \lambda_s kT}\right)^{1/2} \sum_{\upsilon^\prime} exp(-S) \frac {S^{\upsilon^\prime}} {\upsilon^\prime !} exp \left(-\frac {(\Delta G^0 + \lambda_s + \upsilon^\prime \hbar \langle \omega_v \rangle)^2} {4\lambda_s kT} \right)\,\!</math> | ||
When Marcus developed the theory 50 years ago he was looking at electron transfer reactions in solution in which case the “surrounding” was defined by the way the solvents arranged around the sites where electron transfer occurred. For example in organo-metallic systems with ruthenium 2 and ruthenium 3 there will be electron transfer in aqueous solution. There is an orientation of the water molecules surrounding the 2<sup>+</sup> ion that is different from the arrangement around the 3<sup>+</sup> ions. Rearrangement of the solvent involves rotations and translations that are very slow and involve smaller energies. Because these processes are slow its ok to treat them in a classical (simple) way. But intermolecular reorganization energy needs to be taken into account at the quantum level. | When Marcus developed the theory 50 years ago he was looking at electron transfer reactions in solution in which case the “surrounding” was defined by the way the solvents arranged around the sites where electron transfer occurred. For example in organo-metallic systems with ruthenium 2 and ruthenium 3 there will be electron transfer in aqueous solution. There is an orientation of the water molecules surrounding the 2<sup>+</sup> ion that is different from the arrangement around the 3<sup>+</sup> ions. Rearrangement of the solvent involves rotations and translations that are very slow and involve smaller energies. Because these processes are slow its ok to treat them in a classical (simple) way. But intermolecular reorganization energy needs to be taken into account at the quantum level. | ||
Revision as of 10:30, 7 July 2010
| Previous Topic | Return to Transport Properties Menu | Next Topic |
The next question is what happens when the electronic coupling is too small?
Small coupling
The electronic coupling may be small because the crystal structure leads to smaller electronic coupling, or because vibrations disorder the system. In this case the charge carriers become localized and there is polaron formation, leading to geometry relaxation. This is the hopping regime. At a molecular level electron hopping can be cast in the framework of Marcus theory of electron-transfer reactions. Up until recently researchers were using purely phenomenological models.
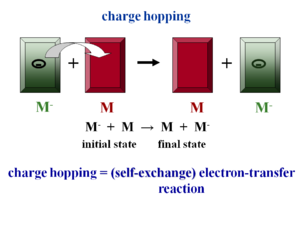
Assume there is molecule that has had an extra electron injected (M-) and has the optimal geometry for the ionized state. Next to it is a neutral molecule (M) with optimal geometry for the neutral state. When the electron hops, the initial molecule goes back to the optimal geometry for the neutral state and the other molecule accepts the electron and adopts the geometry of the ionized state. Charge hopping can be described as a self exchange electron transfer reaction because the chemical nature of the two partners is the same. Therefore you can use Marcus theory of electron transfer to understand charge transport at the molecular level. There is intramolecular relaxation.
In addition to intramolecular relaxation there is also intermolecular relaxation. The distance between a neutral molecule and ionized molecule is larger because the electron density of the ionized molecule is larger. When the electron is transferred to another molecule the formerly ionized molecules becomes neutral and can move closer to the adjacent neutral molecules. This means hop of the electron is coupled to intermolecular relaxation. Ideally we want these couplings to be zero to minimize vibration which disrupts electronic coupling in a band regime.
<embed_document width="35%" height="300">http://depts.washington.edu/cmditr/media/intermol_relax.pdf</embed_document>
Intramolecular Reorganization Energy
Intramolecular reorganization energy is the energy cost due to geometry modifications to go from a neutral to a charged oligomer and vice versa. It is one of the key characteristics that control charge mobility in organic electronics.
Reorganizatin energy can be stated with the Marcus equation:
- <math>k_{ET} =( \frac {4 \pi^2} {h} ) t^2 ( \frac {1} {4 \pi \lambda_s kT} )^{1/2} \sum_{v^\prime} exp(-S) \frac {S^ {v^\prime}} {v^' !} exp (-\frac {( \Delta G^0 + \lambda_S + V^' \hbar \langle \omega_v \rangle )^2}{4 \lambda_SkT}) \,\!</math>
Where
- <math>k_{ET}\,\!</math> is the electron transfer rate
- <math>t\,\!</math> is the electronic coupling between the states
- <math>\Delta G^0\,\!</math> is the Gibbs free energy change
- <math>\lambda_s\,\!</math> is the reorganization energy
- <math>S=\frac {\lambda_i} {\hbar \langle \omega_v \rangle}\,\!</math>
The lower the reorganization energy terms λ i, the smaller the geometry relaxations and the higher the electron transfer rate (kET). If the geometry of the initial molecule, which is in the ionized state, and the geometry of the final molecule, which is in the neutral state, are very similar then there can be electron transfer without having to wait for vibrations. If they are very different geometries then the molecule has to wait until vibrations bring the acceptor into a shape that is more similar to the donor. Electron transfer is activated process because it requires vibration that will prepare the system so that the geometries are equivalent and the electron move.
See Wikipedia on Reorganization Energy
Potential Energy Surfaces
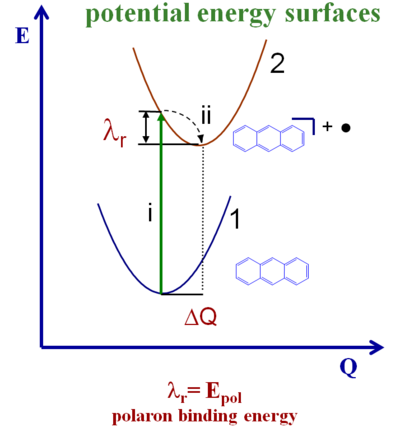
The diagram shows the potential energy surfaces for an anthracene molecule ground state and the potential energy for the cation (this case looks at hops of holes). As the molecule moves from the neutral state to the ionized state there is a vertical ionization (i). Then there relaxation down to the minimum of the potential energy surface (λ r). During the reverse process there is also a relaxation from the ionized state back down to the neutral state. The total reorganization energy is sum of these two relaxations. For many instances those two relaxation energies are very similar so the reorganization energy can be calculated as simple twice the relaxation energy of each molecule. But there is nothing that forces the potential energy surface for the neutral state to be identical to that of the ionized state. The two surfaces might have different curvatures so the two λ r might differ slightly.
Gas UPS Measurements
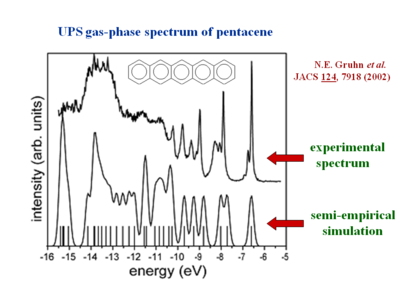
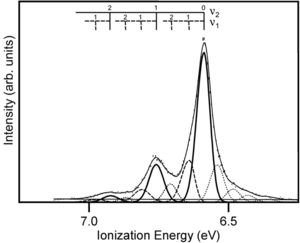
The gas phase UPS was used to measure pentacene. The experimental data shows good agreement with the simulation.
The resolution for gas phase UPS is smaller than .01 eV. The high resolution UPS view shows that the first ionization peak (taking an electron from the HOMO) has vibrations.
Zooming in on the spectra you see a vibronic progression typical of coupling of between vibrational modes as the molecules goes to the optimal geometry of the ionized state. This is similar to the result when looking at absorption spectra for molecules going to an excited state. The vibronic progression can be different. Nothing demands that the optimal ionization geometry needs to be similar to the excited state geometry, but in fact in many pi conjugated systems they are often quite similar. By deconvolution of these vibronic peaks you can arrive at a value for the relaxation energy, and if you double that (assuming the relaxations going from neutral to ionized state, and from ionized to neutral state are the same) you get the reorganization energy.
Experimental estimate for intramolecular reorganization energy for λ I : 0.12 eV
The calculated value (DFT – B3LYP): 0.10 eV
DFT-calculated reorganization energies
The reorganization energy decreases with the increase in size of the molecule. If you plotted these numbers as a function of 1/n the number of π electrons in the system you would get a straight line. Pentacene has a significantly lower reorganization energy than shorter molecules therefore a thin film of pentacene would have a higher electron transfer rate and charge mobility. Pentacene also had a higher electronic coupling than in the smaller molecules in the series.
The DFT-calculated reorganization energy for the oligo-acenes
| Compound | Reorganization Energy | Citation |
|---|---|---|
| naphthalene | 0.187 eV | [[2]] |
| anthracene | 0.137 eV | [[3]] |
| tetracene | 0.114 eV | [[4]] |
| pentacene | 0.098 eV | [[5]] |
| TPD | 0.290 eV | [[6]] |
| siloles | ~ 0.5 eV | [[7]] |
Oligo-acene Trends
Pentacene
Initially longer the oligo-acene the higher the mobility. But as the chains get longer and longer you begin to have localization of charge in the wave function of the ionized state and mobility goes down. Pentacene in the ionized state has a fully delocalized wave function.
Pthalocyanine
Another popular compound with small reorganization energies is pthalocyanines. They have four pyrrole rings that are coupled together by a single conjugated carbon. These can give reorganization energies that are half of that of pentacene. They are popular as pigments in organic semiconductors.
Triphenyldiamine
Triphenyldiamine (TPD) is very often used as a hole transport material. One would hope that a hole transport material would have low reorganization energy and high hole mobility. The reorganization for TPD is actually three times that of pentacene. Reorganization energy in Marcus equation go into an exponential so a factor of three becomes quite significant. Why is it much larger in TPD than in pentacene? In the TPD the geometry relaxations are confined to the biphenyl, binitrogen moiety. The external rings hardly participate in the relaxation that occurs in the ionized state. The wave function of the radical cation is confined to the central part of the molecule. The more confined the ionized state the larger the reorganization energy because an excess of charge or deficit of charge in a small area creates a very large difference. In ionized state in pentacene is spread over 22 π electrons so there is much less perturbation.
Silole
Siloles are used as electron transport materials. The reorganization energy for the ion state is huge; .5 eV. In this case all the geometry relaxation happens in only the silone ring itself. One more electron added to a single ring makes a large difference in bond lengths of .1Å. In the case of pentacene the geometry change is or .01-02Å. So the more you delocalize the wave function of the ionized state the smaller the perturbation and the smaller the reorganization energy.
Limitations of Marcus theory
In order to determine if a molecule will have favorable transport properties in a device you would like to know how mobility changes going from low to high temperature when the material in a thin film or crystalline form. Marcus theory does allow you to do that. The electronic couple is derived for a single crystal structure but the Marcus equation doesn’t consider modifications in electronic coupling that occur with increasing temperature. The intermolecular component of reorganization energy (λ s)(s stands for surrounding) is treated in a purely classical way in Marcus theory.
- <math>k_{ET} = ( \frac {4 \pi^2} { h}) t^2 \left(\frac {1} {4\pi \lambda_s kT}\right)^{1/2} \sum_{\upsilon^\prime} exp(-S) \frac {S^{\upsilon^\prime}} {\upsilon^\prime !} exp \left(-\frac {(\Delta G^0 + \lambda_s + \upsilon^\prime \hbar \langle \omega_v \rangle)^2} {4\lambda_s kT} \right)\,\!</math>
When Marcus developed the theory 50 years ago he was looking at electron transfer reactions in solution in which case the “surrounding” was defined by the way the solvents arranged around the sites where electron transfer occurred. For example in organo-metallic systems with ruthenium 2 and ruthenium 3 there will be electron transfer in aqueous solution. There is an orientation of the water molecules surrounding the 2+ ion that is different from the arrangement around the 3+ ions. Rearrangement of the solvent involves rotations and translations that are very slow and involve smaller energies. Because these processes are slow its ok to treat them in a classical (simple) way. But intermolecular reorganization energy needs to be taken into account at the quantum level.
References
| Previous Topic | Return to Transport Properties Menu | Next Topic |