Difference between revisions of "Electronic Coupling"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| Line 33: | Line 33: | ||
=== Polydiacetylene === | === Polydiacetylene === | ||
[[Image:Polydiacetylene.png|thumb|300px|]] | [[Image:Polydiacetylene.png|thumb|300px|Polydiacetylene structure]] | ||
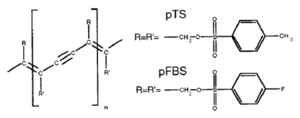
Polydiacetylene crystals have a pattern of double, single, triple, single bonds in their chain. They form perfect crystals when they have bulky side groups like pTS or pFBS. The problem is that because of the bulky side groups chains are pretty far from one another .If you could build a device with a single chain from one electrode to another that would be ideal; the carrier would zip through the chain from one side to another. If the carrier sees a defect it gets stuck because it is difficult to hop to an adjacent chain due to the large distance. Michel Schott has demonstrated macroscopic coherence of a single exciton along an isolated polydiacetylene chain with coherence length over tens of micrometers. These are some of the most perfect π conjugated chains that have been characterized. With a perfect chain the exciton can delocalize across the whole chain forming an exciton band. Polydiacetylene can have and a t along chains of about 2.0 eV. | Polydiacetylene crystals have a pattern of double, single, triple, single bonds in their chain. They form perfect crystals when they have bulky side groups like pTS or pFBS. The problem is that because of the bulky side groups chains are pretty far from one another .If you could build a device with a single chain from one electrode to another that would be ideal; the carrier would zip through the chain from one side to another. If the carrier sees a defect it gets stuck because it is difficult to hop to an adjacent chain due to the large distance. Michel Schott has demonstrated macroscopic coherence of a single exciton along an isolated polydiacetylene chain with coherence length over tens of micrometers. These are some of the most perfect π conjugated chains that have been characterized. With a perfect chain the exciton can delocalize across the whole chain forming an exciton band. Polydiacetylene can have and a t along chains of about 2.0 eV. | ||
Revision as of 13:52, 1 September 2009
| Previous Topic | Return to Transport Properties Menu | Next Topic |
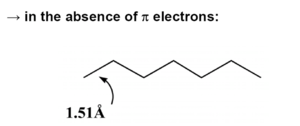
In order have better performance for devices based on electronic semiconductors the charge carrier mobility should be as high a possible and this is accomplished by maximizing the electronic coupling.
Electronic coupling in various molecules
Transpolyacetylene
In perfectly coplanar extended transpolyacetylene chain the electron coupling between adjacent units t (the transfer integral) is on the order of 2.5 – 3eV. Across the entire bandwidth you have about 20 eV.
In actual samples there is conductivity (σ) of 105 S/cm. Conductivity is charge times mobility times charge carrier density. With reasonable assumptions you can calculate a carrier density of 5 x 1021 cm-3 which gives a mobility of μ ~ 100-200 cm2/Vs. The best organic semiconductors with three dimensional lattice and low coupling through vibrations have mobilities of 1000s of cm2/Vs.
Ladder polyparaphylenes
Polyacetylenes chains are somewhat floppy and twists could occur along the chain which decrease order in the system. We can prevent twisting in a chain by adding a bridge carbon at every other ring. This completely flat chain is is known as a ladder polyparaphenylene. T along the chain is ~2.0eV.. Usually charge mobility is measured on a large sample and the charge hops from chain to chain, thus the rate limiting step is the one that is ultimately measured. A group in Delft has developed a technique to measure charge mobility based on microwave measurement that is very fast and therefore they can only see the charge moving over a small distance. This allows them to measure what happens on the chain itself. The intrinsic in-chain carrier mobilities estimated for very long chains: m ~ 600 cm2/Vs. This is a good mobility.
See Prins 2006 [1]
Polydiacetylene
Polydiacetylene crystals have a pattern of double, single, triple, single bonds in their chain. They form perfect crystals when they have bulky side groups like pTS or pFBS. The problem is that because of the bulky side groups chains are pretty far from one another .If you could build a device with a single chain from one electrode to another that would be ideal; the carrier would zip through the chain from one side to another. If the carrier sees a defect it gets stuck because it is difficult to hop to an adjacent chain due to the large distance. Michel Schott has demonstrated macroscopic coherence of a single exciton along an isolated polydiacetylene chain with coherence length over tens of micrometers. These are some of the most perfect π conjugated chains that have been characterized. With a perfect chain the exciton can delocalize across the whole chain forming an exciton band. Polydiacetylene can have and a t along chains of about 2.0 eV.
See Schott 2006 [2]
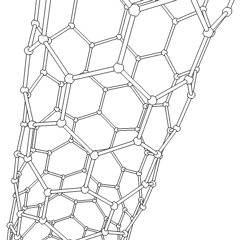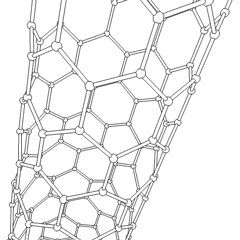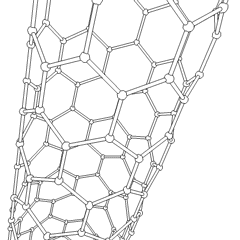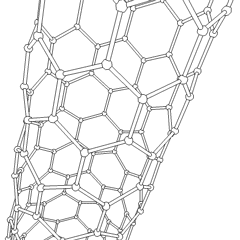
Carbon nanotubes
Carbon nanotubes produce a fairly rigid system because each carbon is bound and little vibration is possible.
t along the chains ~ 2.5 eV
They have exhibited ballistic transport in which the electron moves down the length of the tube without any scattering.
Ballistic transport over 500 nm long nanotubes has bee measured:~ 80,000-100,000 cm2/Vs
See Durkop 2004 [3]
Bulk graphite in bulk graphite: m ~ 15,000 cm2/Vs
These mobilities are greater than any organic semi-conductors. Graphene is a single sheet of graphite which may soon be seen in high performance devices.
See Dressehaus 1996 [4]
In crystalline or well-ordered polymeric materials and nanotubes t along the chains ~ 2.0-3.0 eV
However, in molecular crystals, the relevant electronic coupling is the interchain coupling: t between the chains is one order of magnitude lower or more, that is a few tenths of eV at best.
Thus, localization energy quickly competes with delocalization energy and the band regime is less easy to sustain upon increasing temperature.
References
- ↑ P. Prins, L. Siebbeles, et al., Physical Review Letters 96, 146601 (2006)
- ↑ M. Schott et al., Nature Physics 2, 32 (2006)
- ↑ T. Durkop, S.A. Getty, E. Cobas, and M.S. Fuhrer, NanoLett. 4, 35 (2004)
- ↑ M.S. Dresselhaus, G. Dresselhaus, P.C. Eklund, Science of Fullerenes and Carbon Nanotubes; Academic Press: San Diego, 1996
| Previous Topic | Return to Transport Properties Menu | Next Topic |