Difference between revisions of "Teng-Man Method"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| Line 1: | Line 1: | ||
=== Teng-Mann Method for Measuring Electro-optic coefficient=== | === Teng-Mann Method for Measuring Electro-optic coefficient=== | ||
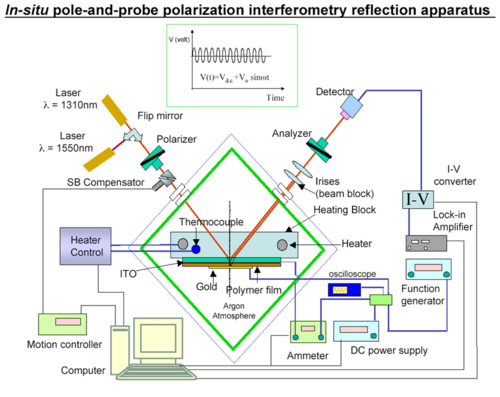
[[Image:teng_mann.png|thumb|500px|Teng-Man Testing configuration]] | [[Image:teng_mann.png|thumb|500px|Teng-Man Testing configuration]] | ||
The Teng - Man method can measure R<sub>33</sub> as the sample is being poled. | |||
R<sub>33</sub> is an elipsometric measurement<ref>http://en.wikipedia.org/wiki/Ellipsometry</ref>. | R<sub>33</sub> is an elipsometric measurement<ref>http://en.wikipedia.org/wiki/Ellipsometry</ref>. A poling voltage is applied to the film while making the elipsometric measurements and looking for changes in the AC signal generated by incident light. The stage can be heated until the film reaches its melting point T<sub>g</sub>. These measurements are made with the materials in a device configuration. The formula for R<sub>33</sub> | ||
:<math>r_{33}= \frac {3\lambda I_m } {4 \pi V_{poly}I_c n^2 } \frac {(n^2 - sin^2 \theta) ^{1/2}}{sin^2 \theta} \approx I_m/ I_c | :<math>r_{33}= \frac {3\lambda I_m } {4 \pi V_{poly}I_c n^2 } \frac {(n^2 - sin^2 \theta) ^{1/2}}{sin^2 \theta} \approx I_m/ I_c | ||
Revision as of 13:30, 7 January 2010
Teng-Mann Method for Measuring Electro-optic coefficient
The Teng - Man method can measure R33 as the sample is being poled. R33 is an elipsometric measurement[1]. A poling voltage is applied to the film while making the elipsometric measurements and looking for changes in the AC signal generated by incident light. The stage can be heated until the film reaches its melting point Tg. These measurements are made with the materials in a device configuration. The formula for R33
- <math>r_{33}= \frac {3\lambda I_m } {4 \pi V_{poly}I_c n^2 } \frac {(n^2 - sin^2 \theta) ^{1/2}}{sin^2 \theta} \approx I_m/ I_c
\,\!</math> where
- <math>I_m\,\!</math> is the amplitude of modulation
- <math>V_{poly}\,\!</math> is the modulation voltage across EO polymer
- <math>I_c\,\!</math> is the half intensity point
- <math>n\,\!</math> is the refractive index of the polymer
and
- <math>V_{poly}= V_{ACtot} \frac {d_{poly}} {d_{poly} + d_{clad}} \cdot \sqrt {\frac {\epsilon_{clad}} {\epsilon _{poly}}}\,\!</math>
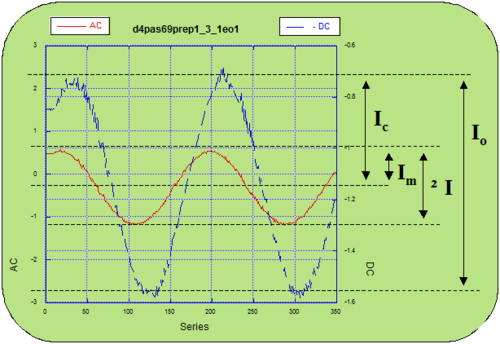
The measured quanitities are:
- <math>I= 2I_M\,\!</math> Modulated Intensity
- <math>I_0 = 2I_C\,\!</math> Output intensity
- <math>V_m = V_0 sin\omega t\,\!</math> Modulation Voltage
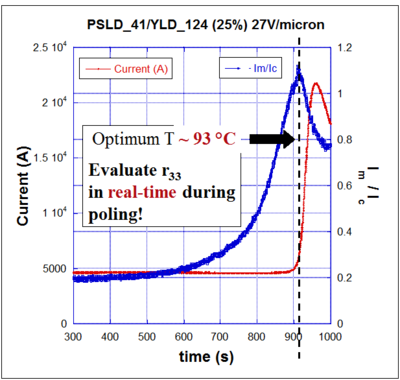
Teng_Mann techniques allows real-time optimization of processing conditions because you can evaluate r33 during the poling process. It is used to confirm that a sample has been poled. The R33 measurement is best used as a relative measure because it can be inaccurate. Use attenuated total reflection ATR to get an accurate absolute measure.
See Khanarian 1996 [2]
See STC-MDITR research project 1.1 [3]
Technique
video to come
Significance
References
- ↑ http://en.wikipedia.org/wiki/Ellipsometry
- ↑ Khanarian, et. al., JOSA B13, 1927 (1996)
- ↑ http://stc-mditr.org/research/oeoaomd/projects/1.111.cfm Measuring R33 with Interferometry