Dispersion and Attenuation Phenomena

Previous Topic

Return to Optical Fibers, Waveguides, and Lasers Menu

Dispersion and attenuation phenomena

As waves propagate they may become wider; this is known as dispersion. The amplitude of waves may decrease; this is known as attenuation. Low attenuation is critical for long distance communication fibers since reamplification of the signal is expensive and complicated. Dispersion causes an overlap of information carrying pulses which decreases the information carrying capacity of an amplitude modulated fiber. We want to design fibers that can carry a very sharp pulse with little dispersion.

Intermodal dispersion

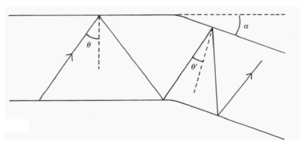
The speed that a ray travels down a fiber depends on its internal angle q. When there are several modes at different angles then the path that each mode takes is different and the arrival time of a bit is different. The time it takes for a mode to move down a fiber:

Minimum for q ~ 90 °

Maxium for q = qc

<math>\Delta \tau_{min} = \frac {Ln_1}{ c sin 90 ^{\circ}} = \frac {Ln_1} {c}\,\!</math>

<math>\Delta \tau_{max} = \frac {Ln_1}{ c sin \theta_ c} = \frac {Ln^2_1} {cn_2}\,\!</math>

This makes sense because if the angle is 90° the mode can propagate down the center without interacting with the cladding.

The maximum difference in time of travel of two modes (one mode at 90° and one at cut-off) can be written:

<math>\Delta \tau^{SI} = \Delta \tau_{max} – \Delta \tau_{min}\,\!</math>

<math>\Delta \tau^{SI} = \frac {L} {c} \frac {n_1} {n_2} (n_1 – n_2)\,\!</math>

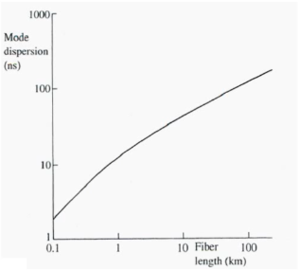
Thus the Dt (and therefore intermodal dispersion ) is proportional to the difference between the indices of refraction. For small fiber lengths up to 1 km the intermodal dispersion is proportional to L.

Example:

For n₁ = 1.48 , n₂ = 1.46 and L = 1km

<math>\Delta \tau^ {SI} = \frac {1 \times 10^3 } {1 \times 10^8} \frac {1.48} {1.46} (1.48 - 1.46)s\,\!</math>

So

<math>\Delta \tau^ {SI} = 6.76 \times 10^{-8}\,\!</math> or 68 ns

This means that for a gigabyte transfer rate after only one km there would be 70 bits that have overlapped and would be lost due to intermodal dispersion.

At distances larger than 1km the intermodal dispersion becomes approximately proportional to the square root of the length and is a significant limiting factor.

The lower rate of increase of dispersion at longer distances is due to mode coupling. Long fibers are not perfectly straight but have small kinks or microbends. A bend acts to realign a mode by slightly changing the angle of incidence over the bended portion. This additive effect tends to recouple or reduce the dispersion of modes that had become dispersed.

Intermodal dispersion may be alleviated by either using a single mode fiber ( a fiber with a V parameter < π/2), or by designing a fiber where the mode velocities are more nearly equal as in a graded index fiber.

Graded index fibers

For graded index fiber in which the indices of refraction of the core and cladding are very close the modal dispersion can be calculated as:

<math>\frac {\Delta \tau ^{GI}_{min}} {\Delta \tau ^ {SI}} \approx \frac {\Delta } {8} << 1\,\!</math>

With

<math>\Delta \approx \frac {n_1 – n_2} {n_1}\,\!</math>

when n₁~n₂

Example

For n1 = 1.48, n2= 1.46 over a distance of 1km

<math>\Delta = \frac {(1.48^2 -1.46^2)} {2 \times 1.48^2}\,\!</math> = 0.0134

Then

<math>\Delta \tau^{GI}\,\!</math> \approx \frac {1 x 10^3 \times 1.48} {8 \times 3 \times 10^8} (0.0134) ^2 = 1.1 \times 10^{-10}s\,\!</math>

This is approximately 600 smaller than the mode dispersion calculated for a step index fiber :<math>\Delta_{\tau}^{SI}= 6.7 \times 10^{-8}s\,\!</math>

Single mode Fibers

In order to achieve single mode propagation the core radius a must be:

<math>A< \frac {2.405 \lambda_0} {2\pi(n^2_1 – n^2_2)^{1/2}}\,\!</math>

In theory the single mode will propagate no matter how small the value of a. However, as a decreases the mode extends increasingly into the cladding, losing energy and thus being highly attenuated. Therefore it is better to keep a very close to maximum value for single mode diameter.

This can be done by making the core and cladding refractive indexes very close together. In practice single mode fibers are made with a numerical aperature (NA) of 0.1. When used with radiation that is typically used in telecommunications 1.3 μ m and 1.6 μ m, single mode fibers have core diameters between 5 μ m and 10 μ m.

Dispersion in single-mode fibers

By using single mode fibers, the problems associated with intermodal dispersion are completely avoided. However there are three other sources of dispersion; material (chromatic) dispersion, profile dispersion and waveguide dispersion.

Material dispersion arises because of the wavelength dependence of the refractive index of the fiber material. Light is never perfectly monochromatic. Any pulse of light consists of a finite spread of wavelengths that travel with a group velocity Vg given by:

<math>V_g = \frac {d \omega} {dk}\,\!</math>

where

<math>\omega = 2 \pi n\,\!</math>

<math>k=\frac { 2\pi}{\lambda}\,\!</math> and lambda is the wavelength in the material

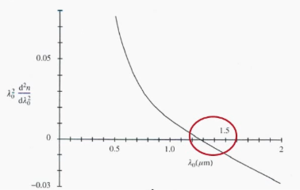
A radiation with finite wavelength spread Δ λ ₀ will have a dispersion over the length (Δ τ _mat) given by

<math>\Delta \tau^{mat} \approx \frac {L \lambda^2_0}{c} \frac {d^2 n} {d \lambda^2_0} \frac {\lambda_0}{\lambda_0}\,\!</math>

The graph shows the variation in the second order derivation of index refraction with respect to wavelength.

For silica the temporal dispersion can be eliminated by using a wavelength of 1.3 μm. It is still pretty good in the range 1.3 to 1.6 which is also critical with respect to attenuation processes.

A semiconductor laser working at 1550 nm has a linewidth of 3 nm will have a Δ τ _mat over 1km of 6.6 x 10^-11 whereas GaAs LED operating at 850 nm and a 50 nm linewidth will have a Δ τ _mat of 4.2 x 10^-9. This clearly shows the superiority of lasers operating at 1550nm.

Profile Dispersion

Profile dispersion arises because of the variation of the quantity Δ with wavelength

<math>\Delta \approx \frac {n_1- n_2} {n_1}\,\!</math>

The index of refraction of different materials will respond differently to changing wavelength. In practice most fibers use silica (with slightly different dopants) for both the core and cladding so the dependence of Δ on wavelength is very small and can be ignored. This is an advantage of having n₁ and n₂ very close to one another.

Waveguide dispersion

Waveguide dispersion is minimal at 1.3μm and 1.4μm wavelength for Si0₂

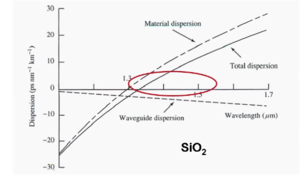
Waveguide dispersion arises because the mode propagation velocity itself depends on wavelength regardless of any refractive index variation of the medium. Waveguide dispersion can not be neglected.

The graph shows both material and waveguide dispersion as a function of wavelength. Temporal dispersion is measured in units of picosecond μm ^-1 km ^-1. Dispersion remains small in the 1.3 to 1.5 μm wavelength range.

Attenuation: intrinsic fiber losses.

attenuation = :<math>\frac { 10 log _10 (P_i / P_f)}{L} dB km ^{-1}\,\!</math>

where

<math>p_i\,\!</math> is the input power

<math>p_f\,\!</math> is the final power

<math>L\,\!</math> is length

Attenuation is expressed in decibels. This would have the unit Bells per meter, and multiplied by 10 it becomes decibels.

Intrinsic losses in silica fibers have two main sources; scattering losses and absorption losses.

Scattering losses

Fibers of silica are an amorphous materials. Crystalline materials would have diffraction losses that would quickly attenuate the beam. Scattering losses is caused by fluctuation in the refractive index through the material with each irregularity acting as point scattering center. The scale of fluctuations is in the order of λ/10. This Rayleigh scattering absorption coefficient varies as λ ^-4. There is a factor of 16 difference in scattering between blue light and red light. The larger the wavelength the smaller the scattering.

Absorption losses

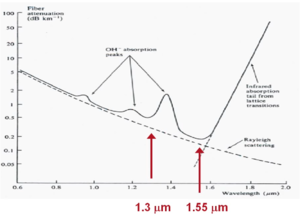
Pure silicon would have virtually no absorption in the critical wavelengths. Absorption losses in the visible and near infrared regions arise mainly from the presence of impurities such as traces of transition metal ions (eg. Fe³⁺ Cu²⁺ or hydoxyl ions (0H^-). Dramatic successes in reducing fiber losses come from better control of impurity concentrations of transition metal ions. It is very difficult to eliminate OH^- bonds (from Si0₂). These are responsible for overtones of vibration and absorption peaks at .95 μm, 0.24 μm and 1.39 μm. The dashed line is the background Rayleigh scattering. Above 1.6 μm there is a rapid increase in infrared absorption from lattice transitions. So there are two windows for absorption at 1.3 μm and 1.55 μm. Thus the combination of all scattering and attenuation phenomena can be optimized for these two wavelengths, which are the common telecommunications wavelengths.

To date some of the lowest attenuations have obtained with GeO₂ - doped SiO₂ fibers which have attenuations of about .2 dB km^-1 at 1.55 μm. This is close to the limit of Rayleigh scattering. This still is high enough that a cross Atlantic cable needs to be reamplified along the way.

Optical Fiber Materials

Optic fiber materials must satisfy certain conditions to be of practical use.

• They must be highly transparent to the radiation being used (the telecommunication frequencies or specific wavelength for example light guides to supply pumped lasers)
• It must be possible and efficient to fabricate the core and cladding structures.
• It must be reasonable flexible

The two types of materials that satisfy these criteria are silica (Si0₂) and various plastics.

See Wikipedia Fiber Optic Materials

Previous Topic

Return to Optical Fibers, Waveguides, and Lasers Menu