Difference between revisions of "Introduction to Third-order Processes and Materials"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| Line 144: | Line 144: | ||
== Second Hyper-polarizability and BOA == | == Second Hyper-polarizability and BOA == | ||
[[Image:Secondpolarizability_boa.png|thumb| | [[Image:Secondpolarizability_boa.png|thumb|500px|Contributions to gamma from various terms]] | ||
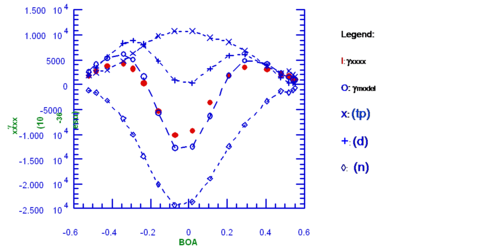
The curve in red shows gamma as a function of BOA as it goes from a polyene limit, through cyanine-like limit, up to a zwitterionic polyene limit. Gamma is calculated using perturbation theory. It starts positive, goes up, goes through zero and has negative peak at the cyanine-like limit and then comes back up and is positive. | The curve in red shows gamma as a function of BOA as it goes from a polyene limit, through cyanine-like limit, up to a zwitterionic polyene limit. Gamma is calculated using perturbation theory. It starts positive, goes up, goes through zero and has negative peak at the cyanine-like limit and then comes back up and is positive. | ||
The simplified perturbation expression for gamma that involves three expressions, dubbed n (negative), tp (two photon) and d (dipolar because it only comes into effect when there is a change in dipole between the ground and the excited state.) | The simplified perturbation expression for gamma that involves three expressions, dubbed '''n''' (negative), '''tp''' (two photon) and '''d''' (dipolar because it only comes into effect when there is a change in dipole between the ground and the excited state.) | ||
:<math>\gamma \propto - \left ( \frac {\mu^{4}_{ge}} {E^{3}_{ge}} \right) + \sum_{e^\prime} \left( \frac {\mu^{2}_{ge} \mu^{2}_{ee^\prime}} {E^{2}_{ge} E_{ge^\prime}} \right ) + \left ( \frac {\mu^{2}_{ge} (\mu_{ee} - \mu_{gg})^{2}} {E^{3}_{ge}} \right )\,\!</math> | :<math>\gamma \propto - \left ( \frac {\mu^{4}_{ge}} {E^{3}_{ge}} \right) + \sum_{e^\prime} \left( \frac {\mu^{2}_{ge} \mu^{2}_{ee^\prime}} {E^{2}_{ge} E_{ge^\prime}} \right ) + \left ( \frac {\mu^{2}_{ge} (\mu_{ee} - \mu_{gg})^{2}} {E^{3}_{ge}} \right )\,\!</math> | ||
Revision as of 10:03, 14 July 2009
| Return to Third-order Processes, Materials & Characterization Menu | Next Topic |
Hyperpolarizability
Gamma is the second hyperpolarizability which is a molecular property. It scales as the cube of the electric field
Nonlinear polarization becomes more important with increasing field strength, since it scales with higher powers of the field. This relates to chi(3), which is a materials property. Chi (3) and gamma can exist in all materials and all molecules, even those which are centrosymmetric materials. (chi(2) can only happen in non centrosymmetric materials).
Taylor Expansion for Polarization
Under normal conditions,
- <math>\alpha_{ij}E .> \beta_{ijk}/2 E·E > \gamma_{ijkl} /6 E·E·E.\,\!</math>
Where
- <math>j\,\!</math> is the coordinate system for the applied field
- <math>i\,\!</math> is the coordinate system for the induced polarization in the molecule
- <math>\alpha\,\!</math> is 3 x 3 tensor
- <math>\beta\,\!</math> is 3 x 3 x 3 tensor with 27 components
- <math>\gamma\,\!</math> is a 3 x 3 x 3 x 3 tensor with 81 components
Thus, there were few observations of NLO effects before the invention of the laser with its associated large electric fields.
Just as alpha is the linear polarizability, the higher order terms beta and gamma (equation (7)) are called the first and second hyperpolarizabilities respectively.
Taylor Expansion for Polarization
Or when all the fields are identical there is a Taylor expansion for bulk polarization:
- <math>P = P_0 + \chi^{(1)}·E + 1/2\chi^{(2)}·· E^2 + 1/6\chi^{(3)}···E^3+ ...\,\!</math> (9)
Some materials such as polyvinylene difluoride when polled can have a bulk polarization in the absence of an applied field.
Just as a molecule can only have a b if it is noncentrosymmetric, a material can only have a chi(2) if the material is noncentrosymmetric (i.e., a centrosymmetry arrangement of noncentrosymmetric molecules lead to zero chi(2)) .
Third-order Nonlinear Polarization of Matter and Third-order NLO Effects
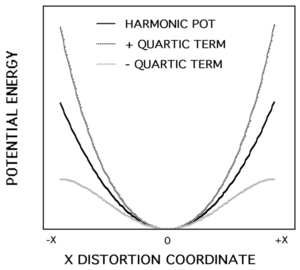
Remember that in χ(2) NLO the harmonic potential has a cubic term that makes one side of the potential somewhat more steep and other side flattened.
With χ(3) we add a restoring force that scales as a displacement to the 4th power. This is an even function. If the correction is added in a positive way the well becomes steeper, adding the correction in a negative way the potential well is more shallow. These curves shown are greatly exaggerated, in reality the deviation would be less than the thickness of the lines as they are drawn. For the most part during normal oscillations the electrons are held within a quadratic potential. Only when there is a large electric field is there deviation of the electron from their resting position to the point where these terms (terms which account for anharmonicity) are manifested in any significant way. When a restoring force of x4 is added to a molecule the polarization deviates from the harmonic potential. A greater displacement means that it is getting harder to polarize the molecule and the greater the difference between the harmonic potential and the quartic potential. A material with a greater susceptibility has a higher refractive index (and a higher dielectric constant). As you polarize this material more and more it becomes harder to polarize and its susceptibility decreases and its refractive index decreases. If when you polarize a material it becomes easier to polarize then the refractive index will decrease.
When a beam of light passes into a material with a higher refractive index it will bend so it focuses closer to the interface between materials (by Snell’s law). The refractive index changes because the intensity of light changes the polarizability, the susceptibility, and therefore the refractive index. In a focusing beam the cross-sectional area of the beam decreases as you approach the focal point and the intensity increases (because there are more photons in a unit area). If the polarizability and susceptibility is proportional to the cube of the electric field then the refractive index will increase. So as a beam becomes focused the added intensity increases the refractive index, causing even more concentrated focus, more intensity and more change in refractive index. This process is called “non linear self focusing”.
All materials (including glass and air) have third order non-linear optical effects. Sometimes these effects can lead to catastrophic self-focusing, leading to the destruction of the materials. This can cause an extremely high intensity of light that can actually damage a laser (it will blow apart). The more perfect the material the less likely you are to blow it apart. When are doing experiments involving frequency tripling researchers use perfect defect free crystals. In laser fusion crystals are used that are as big as a person.
In the case where the polarization decreases with intensity the condition is called self-defocusing. The beam passing through a material has a tendency to spread.
A molecule with a negative beta or a negative χ(2) has a axis or the plane of the molecule has been flipped so that the donor and acceptors are opposite. There will still be an asymmetric polarizability in response to a static electric field. Positive and negative beta lead to the same effects but with opposite signs. However positive and negative gamma and positive and negative χ(3) lead to different effects. Specifically, negative χ(3) leads to self-defocusing, and positive χ(3) leads to self-focusing.
The quartic contribution to the potential has mirror symmetry with respect to the distortion coordinate; as a result both centrosymmetric and noncentrosymmetric materials will have third-order optical nonlinearities.
Third order polarization
If we reconsider equation (14) for the expansion of polarization of a molecule as a function of electric field and assume that the even-order terms are zero (i.e., that the molecule is centrosymmetric) we see that:
- <math>\mu = \mu_0+ \alpha E_0cos(\omega t) + \gamma/6E_{0}^{3}cos3(\omega t) + ...\,\!</math> (22)
If a single field, E(omega,t), is acting on the material, we know from trigonometry that:
- <math>\mu/6E_{0}^{3}cos3(\omega t) = \gamma/6E_{0}^{3}[(3/4)cos(\omega t) + (1/4)cos(3\omega t)]\,\!</math> (23)
These leads to process of frequency tripling in that you can shine light on the molecule and get light at the third harmonic.
thus,
- <math>\mu = \mu_0+ \alpha E_0 cos(omega t) + \gamma /6 E03(3/4)cos(\omega t) + \gamma /6 E03(1/4)cos(3\omega t)\,\!</math> (24)
or:
- <math>\mu= \mu_0+ [\alpha + \gamma /6 E_{0}^{2}(3/4)]E_0cos(\omega t) + \gamma /6 E03(1/4)cos(3\omega t)\,\!</math> (25)
This is an effective polarizability that is related to E02 (the maximum deviation of the sinusoidal electric field) and γ. E02 is always positive. γ can be either positive or negative. Thus by increasing the magnitude of the electric field (light) shining on the materials (with a positive γ) increase the polarizability as the square of the field or decrease the polarizability ( if the γ is negative). So due to the third order effect the linear polarizability can be changed simply by modifying the intensity of the applied light.
Third Harmonic Generation and the Optical Kerr Effect
Thus, the interaction of light with third-order NLO molecules will create a polarization component at its third harmonic.
In addition, there is a component at the fundamental, and we note that the :<math>[\alpha + \gamma /6 E_{0}^{2}(3/4)]\,\!</math> term of equation (25) is similar to the term leading to the linear electrooptic effect or the pockels effect.
Likewise the induced polarization for a bulk material, would lead to third harmonic generation through chi(3), the material susceptibility analogous to gamma.
There are two kinds of Kerr effects. In an optical frequency Kerr effect a very high intensity beam is applied that changes the refractive index of a material.
The quadratic electro-optic effect involves a low intensity beam combined with an applied voltage that can modulate the refractive index.
Four Wave Mixing
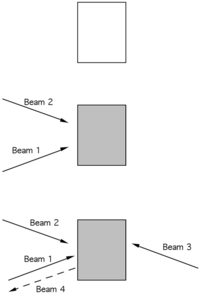
Third harmonic generation is a four wave mixing process. Three waves (electric 1, 2 and 3) interact in material to create a fourth wave. In the case of third harmonic generation with single beam of light the three fields are degenerate; electric field 1 has the same frequency, phase and momentum (k-vect) as electric field 2 and three.
This does not have to be case. There could be three beams with different phases at arbitrary directions, polarizations and frequency components that can all mix and give sums and differences of frequency leading to all kinds of output light.
- <math>\omega 1 + \omega 2 + \omega 3\,\!</math> : this is third harmonic generation
or
- <math>\omega 1 + \omega 2 - \omega 3\,\!</math> : this gives light out at the same frequency (degenerate four wave mixing) as the input leading to the self-focusing effect.
Another interesting manifestation of third-order NLO effect is degenerate four wave mixing in which two beams of light interacting within a material create an interference pattern that will lead to a spatially periodic variation in light intensity across the material. As we have noted before the induced change in refractive index of a third-order nonlinear optical material is proportional to the intensity of the applied field. Thus, if two beams are interacting with a third-order NLO material, the result will be a refractive index grating because of constructive and destructive interference. The diffraction pattern creates areas of high and low light intensity on an NLO material. The areas that are brightest will have an increased refractive index (with a positive χ(3)). At the darkest point the refractive index will have zero change. So if the intensity is changing periodically then the refractive index will have a periodic variation as well. When a third beam is incident on this grating a fourth beam, called the phase conjugate, is diffracted from the grating. This process is called four wave mixing: two writing beams and a probe beam result in a fourth phase conjugate beam.
Degenerate Four-wave Mixing
A potential use of this phenomenon is in phase conjugate optics.
If two beams are directed on a material they create a diffractive index grating. A beam of light has a momentum determined by the direction it is traveling. If you mix the beams of light and do not transfer energy to the material the momentum must be conserved. Two counter propagating beams (with the same phase) have a momentum sum of zero.
Phase conjugate optics takes advantage of a special feature of the diffracted beam: its path exactly retraces the path of one of the writing beams.
- As a result, a pair of diverging beams impinging on a phase conjugate mirror will converge after "reflection".
- In contrast, a pair of diverging beams reflected from an ordinary mirror will continue to diverge.
Thus, distorted optical wavefronts can be reconstructed using phase conjugate optical systems.
Phase Conjugation
Thus, distorted optical wavefronts can be reconstructed using phase conjugate optical systems.
A diverging set of beams reflected off of a normal mirror continues to diverge. (left) A diverging set of beams reflected off of a phase conjugate mirror exactly retrace their original path and are recombined at their point of origin. (right)
Phase Conjugate Mirror
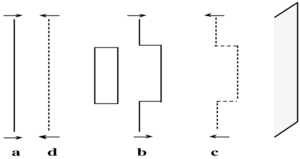
A planar wave (a) passes through a distorting material (b) that introduces an aberration and the light interacts with a phase conjugate mirror (c) creating the phase conjugate wavefront. (d) Phase conjugate wave passes through the distorting material on the reverse path canceling the original aberation thus producing an undistorted wavefront.
A wavefront made up a lot of beams is travelling in direction a through a medium. Some aberration (with lower refractive index) in the material allows a portion of the light to go faster causing a bump in the wavefront. When the wavefront hits the phase conjugate mirror all parts are reversed. The part of the beam that comes into the mirror first ends up leaving last; there is a time reversal. When the reversed beam travel back and encounters the original aberration the distortion is removed.
There are applications for this when looking at distant objects that have passed through a material that is scattering. If you bounce the light off a phase conjugate in two passes and you can get back the original undistorted image. This is useful for targeting applications and for looking at images on the Earth from a satellite where there are distortions due to inhomogeneities the atmosphere. This is a third order non linear optical effect.
See wikipedia http://en.wikipedia.org/wiki/Nonlinear_optics#Optical_phase_conjugation
Second Hyper-polarizability and BOA
The curve in red shows gamma as a function of BOA as it goes from a polyene limit, through cyanine-like limit, up to a zwitterionic polyene limit. Gamma is calculated using perturbation theory. It starts positive, goes up, goes through zero and has negative peak at the cyanine-like limit and then comes back up and is positive.
The simplified perturbation expression for gamma that involves three expressions, dubbed n (negative), tp (two photon) and d (dipolar because it only comes into effect when there is a change in dipole between the ground and the excited state.)
- <math>\gamma \propto - \left ( \frac {\mu^{4}_{ge}} {E^{3}_{ge}} \right) + \sum_{e^\prime} \left( \frac {\mu^{2}_{ge} \mu^{2}_{ee^\prime}} {E^{2}_{ge} E_{ge^\prime}} \right ) + \left ( \frac {\mu^{2}_{ge} (\mu_{ee} - \mu_{gg})^{2}} {E^{3}_{ge}} \right )\,\!</math>
N the transition dipole moment between the ground and the initial site (coming in at the 4th power) divided by the energy gap between those two states.
Ge is the transition dipole moment between and the excited state squared, and between the excited state and a higher lying excited state squared.
Two energy terms goes between the ground and the excited state squared and the other between the ground and the higher excited state.
The final term should look a lot like beta. The difference in dipole moment is squared so that it always positive, the energy term is cubed. It starts at the zero, increases to maximum and then return to zero.
The calculation gives gamma using this model which is plotted as open blue circle. These look a lot like the red dots.
Each term contributes to the resulting curve for gamma.
Third-order Nonlinear Optical Properties of Polarized Polyenes
Beta carotene is the pigment found in margarine. By adding stronger and stronger acceptors it be polarized. Lambda max increases by a factor of 45.
The real part of the refractive index is related to how light is diffracted, the imaginary part is related to absorption of light.
The same is true about gamma. The real part refers to how the refractive index is changed as light of a given intensity goes through it. The imaginary part is related to two photon absorption. Molecules will have both real and imaginary parts. In order to make useful devices like the Mach Zehnder interferometer you want the index of refraction to change but don’t want to lose light in the material. ELO materials can lose transparency due to absorption or scattering. They can also lose transparency at a high intensity is due to the process of two photon absorption. Dipolar molecules tend to have large positive gamma but also tend to have high two photon absorption cross sections.
Recently we have discovered that molecules with negative gamma that have verge large real parts that lead to interesting optical effects and that in certain spectral regions their imaginary part is almost zero so there is no light lost due to two photon absorption. These are good candidates for all optical switching applications because until now molecules with high chi(3) have had a high a loss due to two photon absorption.
| Return to Third-order Processes, Materials & Characterization Menu | Next Topic |