Electronic States vs Molecular Levels

Return to Band Structure Menu

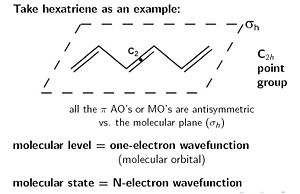
The literature can be confusing in using the terminology of electronic states vs electrical levels. There is always an identity symmetry (E). The hexatriene molecule is symmetrical around the C2 axis. The C2 axis is perpendicular from the plane of the molecule. A rotation of 180 degrees brings the same structure. The sigma h denotes symmetry above and below the plane, there must be the same electronic density above the plane as below. There is also an inversion symmetry (i) where the C2 axis meets the plane . These together have a point group called C2h.

Molecular level is a one electron wavefunction which is by definition a molecular orbital. Molecular levels corresponds to molecular orbitals (HOMO, LUMO etc).

Molecular states which is what you can observe is a wavefunction that results from all the electrons in the molecule.

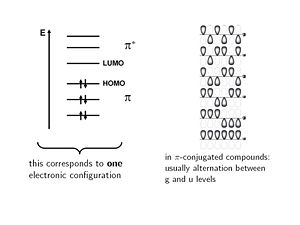
The electronic configuration is shown with six molecular orbitals, three of which on the pi level are fully occupied. You can build many more configurations in which individual electrons move up to the pi* level, these are called singly excited. You can also elevate two electrons from occupied levels into unoccupied levels, called doubly excited configurations. The way you put the electrons into the orbitals corresponds to electronic configurations.

The wavefunctions can be classified according their symmetry. The lowest level is the fully bonding an is unsymmetrical; it is labeled ungehade (u). The next level up has a node in the middle and it is symmetral and is labeled gerade (g). In π conjugated systems molecular orbitals alternative between gerade (g - gerade is german for even) and ungerade (u - ungerade is german for odd)with each level.

One can generate other electronic configurations by promoting one or more electrons from occupied levels to unoccupied levels. One promotion is known as "singly excited configuration", and two or three are doubly or triply excited.

An electronic state is described by a weighted combination of electronic configurations. In many instances however the ground state and the lowest excited states can be described by only one or very dominant configurations.

In the example above the ground state with all π and σ levels doubly occupied is denoted Ag symmetry, or 1 Ag. This is also called S₀.

The lowest ground stat π excited states can noted as Ag or Bu symmetry.

The 1 Bu excited state is dominated by a (singly excited) configuration with promotion of one electron from HOMO to LUMO. Suppose you shine a light on a molecule and cause an electron to enter the excited state. In order for the transition to be allowed you need to have different symmetries for the ground state and for the excited state. If the ground state is gerade (even) the excited state must be ungerade (odd). This is because transition dipole operator is an odd function.

1Bu Excited state

This can be noted using Dirac notation. The integral over all space of initial state gerade (g) the the dipole operator (r) and the wave function for the final state (u). In order for the integral to non zero the product for all three terms must be even for a level. Therefore the transition to the 1Bu excited state is possible. If there were a transition to a gerade excited state the product (g, r and g) would be odd and therefore the integral would be zero. The probability for an electron to go from the 1Ag to the 2Ag state is taken as the square of the transition dipole function, so if the function is zero, its square is zero and therefore the probability of the transition is zero. If an molecule has no symmetry you can go from the ground state to any excited state. As soon as a molecule has symmetry there are selection rules that apply. Experimentally it is impossible to excite a polyene molecule to the 2Ag state. The transition dipole is zero, this is known as a forbidden transition. The fact that a transition dipole is non-zero does not tell you about the probability in itself; it could be exceedingly small probability. However a non-zero transition dipole has at least some probability and therefore is not forbidden transition.

For along time the one-photon allowed 1Bu was thought to be the lowest possible excited state for a polyene molecule also called S1 (the lowest singlet excted state). See the papers by Hudson and Kolher that showed that the lowest excited state is actually the 2Ag.

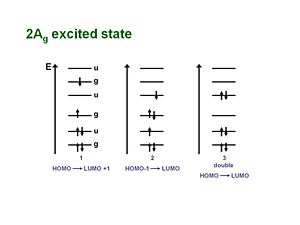
2Ag excited state

For along time the one-photon allowed 1Bu was thought to be the lowest possible excited state for a polyene molecule also called S1 (the lowest singlet excted state). But the papers by Hudson and Kolher that showed that the lowest excited state in a long polyene is actually the 2Ag (the second state of Ag symmetry). There is not a single electronic state that dominates that wave function. One involves the promotion from HOMO to the LUMO plus 1 which is gerade. A second case promotes an electron from the HOMO-1 to the LUMO, which is also gerade. There is also a doubly excited situation in which two electrons are promoted from the HOMO to the LUMO resulting in a gerade state.

As long as they have the same symmetries they can mix. These three configurations have approximately the same energies so they can mix strongly. They are one photon forbidden (but two photon allowed). This results in a 2Ag state that is lower energetically than the 1Bu state, thus it should be considered the S1 state.

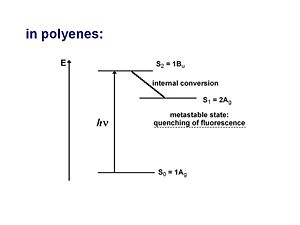
You can not have an optical transition from the 1Ag to the 2Ag state but you will see absorption indicating a transition to the 1Bu state which is higher in energy. From here it can vibrate and lower its energy through the process of internal conversion to the 2Ag state and then stay there because the transition to the 1Ag state is forbidden. This results in a metastable state which is observed as quenching of the luminescence.