Difference between revisions of "Sigma and pi Orbitals"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| Line 2: | Line 2: | ||
[[Polarization and Polarizability|Next Topic]] | [[Polarization and Polarizability|Next Topic]] | ||
[[Image:2sigma_orbitals.png|thumb|300px|Hydrogen 1 and Hydrogen 2 combine to form a new molecular orbital.]] | [[Image:2sigma_orbitals.png|thumb|300px|Hydrogen 1 and Hydrogen 2 combine to form a new molecular orbital.]] | ||
=== Molecular Orbital Theory === | |||
Molecular orbital theory was developed in the early part of the last century to help rationalize why bonds form and to explaint the properties of molecules. In molecular orbital theory the atomic orbitals from each atom can overlap with those on other atoms. Since the atomic orbitals are wavefunctions and behave like waves it is possible for them to overlap in a constructive manner to form a bonding orbital. | Molecular orbital theory was developed in the early part of the last century to help rationalize why bonds form and to explaint the properties of molecules. In molecular orbital theory the atomic orbitals from each atom can overlap with those on other atoms. Since the atomic orbitals are wavefunctions and behave like waves it is possible for them to overlap in a constructive manner to form a bonding orbital. | ||
| Line 14: | Line 16: | ||
[[Image:H2_antibonding_orbital.png|thumb|300px|]] | [[Image:H2_antibonding_orbital.png|thumb|300px|]] | ||
Note theat the electron density is higher between the nuclei in the | Note theat the electron density is higher between the nuclei in the bonding molecular orbital and the that the orbital is stabilized, that is lower in energy relative to the two isolated hydrogren atoms. The sign of both wavefunctions is positive. There is a decreased electron density between the atoms in the antibonding molecular orbital and the orbital is destabilized, that is higher in energy, than the two isolated hydrogen atoms. In very simple molecular orbital theory we treat the destabilization energy of the antibonding orbital as identical to the stabilization energy of the bonding orbital but in fact it is slightly more destabilized than the bond orbital is stabilized. | ||
=== Orbital Overlap === | |||
The amount of stabilization or destabilization is referred to a their orbital overlap. Mathematically the overlap is an integral of from negative infinity to positive infinity of a product of two wavefunctions over all space. | |||
\int_limits{\infty} {-\infty} \Psi_1^* |Psi_2 | |||
Revision as of 09:51, 19 May 2009
Return to Molecular Orbitals Menu | Next Topic
Molecular Orbital Theory
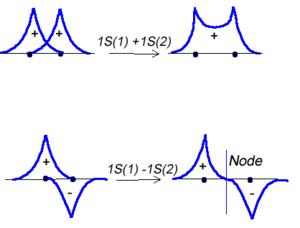
Molecular orbital theory was developed in the early part of the last century to help rationalize why bonds form and to explaint the properties of molecules. In molecular orbital theory the atomic orbitals from each atom can overlap with those on other atoms. Since the atomic orbitals are wavefunctions and behave like waves it is possible for them to overlap in a constructive manner to form a bonding orbital.
<math>\Psi_{new} = \Psi_1 + \Psi_2\,\!</math>
Or the two functions can combine in a destructive manner.
<math>\Psi_{new} = \Psi_1 - \Psi_2\,\!</math>
This is sometimes referred to as Linear Combination of Atomic Orbitals (LCAO). When there is a destructive combination of the two wave results in a node between the two atoms where the there is a zero probability of finding the electron. The first case is known as a bonding orbital and the bottom case is known as an anti-bonding orbital.
Note theat the electron density is higher between the nuclei in the bonding molecular orbital and the that the orbital is stabilized, that is lower in energy relative to the two isolated hydrogren atoms. The sign of both wavefunctions is positive. There is a decreased electron density between the atoms in the antibonding molecular orbital and the orbital is destabilized, that is higher in energy, than the two isolated hydrogen atoms. In very simple molecular orbital theory we treat the destabilization energy of the antibonding orbital as identical to the stabilization energy of the bonding orbital but in fact it is slightly more destabilized than the bond orbital is stabilized.
Orbital Overlap
The amount of stabilization or destabilization is referred to a their orbital overlap. Mathematically the overlap is an integral of from negative infinity to positive infinity of a product of two wavefunctions over all space.
\int_limits{\infty} {-\infty} \Psi_1^* |Psi_2