Difference between revisions of "Molecular Dynamics Simulation"
Cmditradmin (talk | contribs) m (→Force Field) |
Cmditradmin (talk | contribs) m (→References) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 25: | Line 25: | ||
The molecular dynamics force field can be defined as an equation and set of constants that describe the potential energy from all bonded and non-bonded interactions in an atomic system. Different force fields can be found in the literature for a wide range of molecular system. They vary in both the functional form and the parameter values, all with varying degrees of specificity in the atoms, molecules and materials to which they can be applied. A simple functional form for a force field (Class 1) is defined in equation (1) below.5 | The molecular dynamics force field can be defined as an equation and set of constants that describe the potential energy from all bonded and non-bonded interactions in an atomic system. Different force fields can be found in the literature for a wide range of molecular system. They vary in both the functional form and the parameter values, all with varying degrees of specificity in the atoms, molecules and materials to which they can be applied. A simple functional form for a force field (Class 1) is defined in equation (1) below.5 | ||
<math>V_{FF}=\mathrm{\Sigma}_{bonds}\frac{1}{2}K_{b,ij}\left(b_{ij}-b_{o,ij}\right)^2+\mathrm{\Sigma}_{angles}\frac{1}{2}K_{\theta,ijk}\left(\theta_{ijk}-\theta_{o,ijk}\right)^2+\mathrm{\Sigma}_{impropers}\frac{1}{2}K_{\zeta,ijkl}\left(\zeta_{ijkl}-\zeta_{o,ijkl}\right)^2+\ \mathrm{\Sigma}_{dihedrals}K_{\phi,ijkl}\left(1+cos{\left(n\phi_{ijkl}-\delta_n\right)}\right)+\ \mathrm{\Sigma}_{pairs}\left[4\epsilon_{ij}\left[\left(\frac{\sigma_{ij}}{r_{ij}}\right)^{12}-\left(\frac{\sigma_{ij}}{r_{ij}}\right)^6\right]+K_{Coulomb}\frac{q_iq_j}{\kappa r_{ij}}\right]</math> | |||
<math>V_{FF}=\mathrm{\Sigma}_{bonds}\frac{1}{2}K_{b,ij}\left(b_{ij}-b_{o,ij}\right)^2+\mathrm{\Sigma}_{angles}\frac{1}{2}K_{\theta,ijk}\left(\theta_{ijk}-\theta_{o,ijk}\right)^2+\mathrm{\Sigma}_{impropers}\frac{1}{2}K_{\zeta,ijkl}\left(\zeta_{ijkl}-\zeta_{o,ijkl}\right)^2+\ \mathrm{\Sigma}_{dihedrals}K_{\phi,ijkl}\left(1+cos{\left(n\phi_{ijkl}-\delta_n\right)}\right)+\ \mathrm{\Sigma}_{pairs}\left[4\epsilon_{ij}\left[\left(\frac{\sigma_{ij}}{r_{ij}}\right)^{12}-\left(\frac{\sigma_{ij}}{r_{ij}}\right)^6\right]+K_{Coulomb}\frac{q_iq_j}{\kappa r_{ij}}\right]</math>(1) | |||
where: | where: | ||
<math>K_(b,ij)</math> = bond energy constant for bonded atoms i and j, units of energy/(distance^2 ) | <math>K_(b,ij)</math> = bond energy constant for bonded atoms i and j, units of energy/(distance^2 ) | ||
b_ij = distance between bonded atoms i and j, units of distance | <math>b_ij = </math>distance between bonded atoms i and j, units of distance | ||
<math>K_{b,ij} = </math>bond energy constant for bonded atoms i and j, units of \frac{energy}{distance^2} | |||
<math>b_{ij} =</math> distance between bonded atoms i and j, units of distance | |||
<math>b_{o,ij} =</math> bond distance constant for bonded atoms i and j, units of distance | |||
<math>K_{\theta,ijk} = </math>angle energy constant for bonded atoms i, j, and k, units of \frac{energy}{degrees^2} | |||
<math>\theta_{ijk} = </math>angle between bonded atoms i, j, and k, units of degrees | |||
<math>\theta_{o,ijk} =</math> angle constant for bonded atoms i, j, and k, units of degrees | |||
<math>K_{\zeta,ijkl} =</math> improper dihedral energy constant for bonded atoms i, j, k, and l, units of \frac{energy}{degrees^2} | |||
<math>\zeta_{ijkl} = </math>improper angle for bonded atoms i, j, k, and l, units of degrees | |||
<math>\zeta_{o,ijkl} =</math> improper angle constant for bonded atoms i, j, k, and l, units of degrees | |||
<math>K_{\phi,ijkl} =</math> dihedral energy constant for linearly bonded atoms i, j, k, and l, units of energy | |||
<math>n = </math>integer | |||
<math>\phi_{ijkl} =</math> dihedral angle for linearly bonded atoms i, j, k, and l, units of degrees | |||
<math>\delta_n = </math>dihedral angle constant for linearly bonded atoms i, j, k, and l, units of degrees | |||
<math>\epsilon_{ij} =</math> Lennard-Jones energy constant for non-bonded atoms i and j, units of energy | |||
<math>\sigma_{ij} =</math> Lennard-Jones distant constant for non-bonded atoms i and j, units of distance | |||
<math>r_{ij} =</math> distance between non-bonded atoms i and j, units of distance | |||
<math>K_{Coulomb} =</math> Coulomb constant,\<math> 8.988\ \times\ {10}^9\frac{Nm^2}{C^2}</math> | |||
<math>q_i, q_j = </math>charges of non-bonded atoms i and j, units of elementary\ charge | |||
<math>\kappa =</math> dielectric constant, unitless | |||
For an interactive thorough exploration of this force field, visit https://interactive-md-ff.herokuapp.com/. | For an interactive thorough exploration of this force field, visit https://interactive-md-ff.herokuapp.com/. | ||
| Line 85: | Line 92: | ||
The full length of the simulation in time (e.g. 1 nanosecond) is broken down into discrete time steps (e.g. 1 femtosecond). At each time step, the bonded and non-bonded forces on each atom are summed using equations (1) and (2), and the atoms ‘step’ forward in position and time in response to those forces. One method to approximate an atom’s next position is the Velocity-Verlet algorithm shown in equations (3) and (4).6 This integrator computes an atom’s position and velocity at every time step. By stringing this information together at every time step over the duration of the simulation (e.g. 1,000,000 steps of 1 fs each for a 1 ns simulation), a trajectory of the atomic motions can be created. This data can then be analyzed to uncover information about the molecular-level behavior in the system (e.g. diffusion, mean squared displacement). | The full length of the simulation in time (e.g. 1 nanosecond) is broken down into discrete time steps (e.g. 1 femtosecond). At each time step, the bonded and non-bonded forces on each atom are summed using equations (1) and (2), and the atoms ‘step’ forward in position and time in response to those forces. One method to approximate an atom’s next position is the Velocity-Verlet algorithm shown in equations (3) and (4).6 This integrator computes an atom’s position and velocity at every time step. By stringing this information together at every time step over the duration of the simulation (e.g. 1,000,000 steps of 1 fs each for a 1 ns simulation), a trajectory of the atomic motions can be created. This data can then be analyzed to uncover information about the molecular-level behavior in the system (e.g. diffusion, mean squared displacement). | ||
r(t+ | <math>r\left(t+\mathrm{\Delta t}\right)=r\left(t\right)+\mathrm{\Delta\ t}\ v\left(t\right)+\frac{\mathrm{\Delta}t^2F(t)}{2m}</math> (3) | ||
v(t+ | <math>v\left(t+\mathrm{\Delta t}\right)=v\left(t\right)+\frac{\mathrm{\Delta t}(F\left(t\right)+\ F\left(t+\mathrm{\Delta t}\right))}{2m}\ </math>(4) | ||
where: | where: | ||
| Line 115: | Line 122: | ||
==References== | ==References== | ||
# A. Arbe, F. Alvarez and J. Colmenero, Neutron scattering and molecular dynamics simulations: synergetic tools to unravel structure and dynamics in polymers, Soft Matter, 2012, 8, 8257. | |||
# J. N. Israelachvili, Intermolecular and Surface Forces, Elsevier Inc., 3rd ed., 2011. | |||
# D. P. McMahon, D. L. Cheung, L. Goris, J. Dacuña, A. Salleo and A. Troisi, Relation between microstructure and charge transport in polymers of different regioregularity, J. Phys. Chem. C, 2011, 115, 19386–19393. | |||
# P. C. Tapping, S. N. Clafton, K. N. Schwarz, T. W. Kee and D. M. Huang, Molecular-Level Details of Morphology-Dependent Exciton Migration in Poly(3-hexylthiophene) Nanostructures, J. Phys. Chem. C, 2015, 119, 7047–7059. | |||
# M. Moreno, M. Casalegno, G. Raos, S. V. Meille and R. Po, Molecular Modeling of Crystalline Alkylthiophene Oligomers and Polymers, J. Phys. Chem. B, 2010, 114, 1591–1602. | |||
# D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, San Diego, 2nd edn., 2002. | |||
# K. N. Schwarz, T. W. Kee and D. M. Huang, Coarse-grained simulations of the solution-phase self-assembly of poly(3-hexylthiophene) nanostructures, Nanoscale, 2013, 5, 2017. | |||
Latest revision as of 10:53, 12 May 2020
Molecular Dynamics Simulations
Introduction
Molecular dynamics (MD) simulations are a computational tool for exploring molecular scale structure and dynamics in a wide variety of materials. They have been used to study solutions, bulk materials, interfaces, crystal structures, proteins, and polymers. Researchers can use this computational approach to explore properties and behaviors of these materials at small length and time scales that are not always directly accessible by experimental methods. It can also provide new perspectives or additional information about complex phenomena observed in experiments.1 MD can be used to study diffusion, polymer self-assembly, preferred molecular conformations, and more.
There is a diverse and complex set of bonded and non-bonded interactions between atoms and molecules that arise from electromagnetic forces.2 The most accurate method for modeling these interactions is a quantum mechanical approach. However, these ab initio calculations are computationally expensive and are therefore limited in the time and length scales at which they can model molecular systems. Molecular dynamics simulations instead approximate these interactions using classical mechanics. While some accuracy is lost, these systems are still able to capture larger-scale behaviors on the order of picoseconds to milliseconds (ps-ms) and Angstroms to millimeters (Å-mm), and provide researchers with useful information.
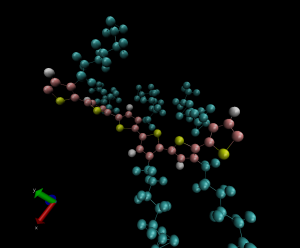
Figure 1. Snapshot from a molecular dynamics simulation of poly(3-hexylthiophene) (P3HT). Alkyl side chains (carbon and hydrogen atoms) are shown in blue, backbone hydrogen atoms are shown in white, backbone carbon atoms are shown in red, and sulfur atoms are shown in yellow.
Applications in Clean Energy Research
Molecular dynamics simulations have been used to study materials in many areas of clean energy research, such as solar cell technologies or batteries. These tools can give researchers a deeper understanding of the materials and can also help researchers design improved materials for new technologies. For example, molecular dynamics simulations have been critical in understanding charge transport mechanisms in conjugated polymers (CPs), semiconducting materials that are found in the active layers of organic photovoltaics (OPVs). Their structure is comprised of a conjugated backbone with alternating double and single bonds that enable charge transport. Side chains are also included in the polymer structure to improve their solubility. While not yet as efficient, these polymers enable flexible, lightweight, and solution-processable alternatives to more prevalent inorganic equivalents.
Poly(3-hexylthiophene) (P3HT) is a common, well-studied conjugated polymer in the field. It provides a model system for studying the molecular behavior of CPs and how it relates to their macroscopic performance. In the work of McMahon, et al., researchers used atomistic molecular dynamics simulations of P3HT to understand the effects of structural defects in the polymer chain on the charge delocalization in the material.3 MD simulations were used to capture large-scale molecular structures at various time points along the trajectory. These ‘frozen’ structures were then fed to more accurate quantum mechanic calculations to understand the charge movement. Another group, Tapping and coworkers, used coarse-grained molecular dynamics to study P3HT on an even larger scale.4 They paired the coarse-grained structures of self-assembled P3HT nanofibers in solution with ab-initio approaches to track exciton movement through the fiber.
Fundamentals of Molecular Dynamics Simulations
Force Field
Atoms in a molecular dynamics simulation will move in response to the sum of bonded and non-bonded interactions with neighboring atoms. These include bonds, van der Waals forces, steric repulsion and Coulomb forces. There are also contributions from the angles and dihedrals (planarity) formed by three or more bonded atoms. All bonded and non-bonded interactions are approximated with equations of various functional forms and constants derived from ab initio calculations or empirical fitting approaches. For some parameters, energy as a function of a conformational change (e.g. distance between two atoms) is fit to determine the relevant parameters (e.g. bond energy and distance constants). Other parameters are modified to recreate macroscopic properties of the system (e.g. density) during a simulation.
The molecular dynamics force field can be defined as an equation and set of constants that describe the potential energy from all bonded and non-bonded interactions in an atomic system. Different force fields can be found in the literature for a wide range of molecular system. They vary in both the functional form and the parameter values, all with varying degrees of specificity in the atoms, molecules and materials to which they can be applied. A simple functional form for a force field (Class 1) is defined in equation (1) below.5
<math>V_{FF}=\mathrm{\Sigma}_{bonds}\frac{1}{2}K_{b,ij}\left(b_{ij}-b_{o,ij}\right)^2+\mathrm{\Sigma}_{angles}\frac{1}{2}K_{\theta,ijk}\left(\theta_{ijk}-\theta_{o,ijk}\right)^2+\mathrm{\Sigma}_{impropers}\frac{1}{2}K_{\zeta,ijkl}\left(\zeta_{ijkl}-\zeta_{o,ijkl}\right)^2+\ \mathrm{\Sigma}_{dihedrals}K_{\phi,ijkl}\left(1+cos{\left(n\phi_{ijkl}-\delta_n\right)}\right)+\ \mathrm{\Sigma}_{pairs}\left[4\epsilon_{ij}\left[\left(\frac{\sigma_{ij}}{r_{ij}}\right)^{12}-\left(\frac{\sigma_{ij}}{r_{ij}}\right)^6\right]+K_{Coulomb}\frac{q_iq_j}{\kappa r_{ij}}\right]</math>(1)
where:
<math>K_(b,ij)</math> = bond energy constant for bonded atoms i and j, units of energy/(distance^2 )
<math>b_ij = </math>distance between bonded atoms i and j, units of distance
<math>K_{b,ij} = </math>bond energy constant for bonded atoms i and j, units of \frac{energy}{distance^2}
<math>b_{ij} =</math> distance between bonded atoms i and j, units of distance
<math>b_{o,ij} =</math> bond distance constant for bonded atoms i and j, units of distance
<math>K_{\theta,ijk} = </math>angle energy constant for bonded atoms i, j, and k, units of \frac{energy}{degrees^2}
<math>\theta_{ijk} = </math>angle between bonded atoms i, j, and k, units of degrees
<math>\theta_{o,ijk} =</math> angle constant for bonded atoms i, j, and k, units of degrees
<math>K_{\zeta,ijkl} =</math> improper dihedral energy constant for bonded atoms i, j, k, and l, units of \frac{energy}{degrees^2}
<math>\zeta_{ijkl} = </math>improper angle for bonded atoms i, j, k, and l, units of degrees
<math>\zeta_{o,ijkl} =</math> improper angle constant for bonded atoms i, j, k, and l, units of degrees
<math>K_{\phi,ijkl} =</math> dihedral energy constant for linearly bonded atoms i, j, k, and l, units of energy
<math>n = </math>integer
<math>\phi_{ijkl} =</math> dihedral angle for linearly bonded atoms i, j, k, and l, units of degrees
<math>\delta_n = </math>dihedral angle constant for linearly bonded atoms i, j, k, and l, units of degrees
<math>\epsilon_{ij} =</math> Lennard-Jones energy constant for non-bonded atoms i and j, units of energy
<math>\sigma_{ij} =</math> Lennard-Jones distant constant for non-bonded atoms i and j, units of distance
<math>r_{ij} =</math> distance between non-bonded atoms i and j, units of distance
<math>K_{Coulomb} =</math> Coulomb constant,\<math> 8.988\ \times\ {10}^9\frac{Nm^2}{C^2}</math>
<math>q_i, q_j = </math>charges of non-bonded atoms i and j, units of elementary\ charge
<math>\kappa =</math> dielectric constant, unitless
For an interactive thorough exploration of this force field, visit https://interactive-md-ff.herokuapp.com/.
Classical mechanics are used to determine the forces each atom experiences due to these bonded and non-bonded interactions as well as the direction and speed at which they move in response to those forces. Following Newton’s second law of motion and utilizing the force field in equation (1), the force can be defined as1,6: <math>F=ma=-\frac{\delta V_{FF}}{\delta r}</math>(2)
where: F = force
m = mass
a = acceleration
This equation can then be solved for the position and velocity of all atoms at every time step during the simulation. This algorithm is known as the integrator.
Integrator
The full length of the simulation in time (e.g. 1 nanosecond) is broken down into discrete time steps (e.g. 1 femtosecond). At each time step, the bonded and non-bonded forces on each atom are summed using equations (1) and (2), and the atoms ‘step’ forward in position and time in response to those forces. One method to approximate an atom’s next position is the Velocity-Verlet algorithm shown in equations (3) and (4).6 This integrator computes an atom’s position and velocity at every time step. By stringing this information together at every time step over the duration of the simulation (e.g. 1,000,000 steps of 1 fs each for a 1 ns simulation), a trajectory of the atomic motions can be created. This data can then be analyzed to uncover information about the molecular-level behavior in the system (e.g. diffusion, mean squared displacement).
<math>r\left(t+\mathrm{\Delta t}\right)=r\left(t\right)+\mathrm{\Delta\ t}\ v\left(t\right)+\frac{\mathrm{\Delta}t^2F(t)}{2m}</math> (3)
<math>v\left(t+\mathrm{\Delta t}\right)=v\left(t\right)+\frac{\mathrm{\Delta t}(F\left(t\right)+\ F\left(t+\mathrm{\Delta t}\right))}{2m}\ </math>(4)
where: r = atomic position v = velocity F = force m = atomic mass t = current time in simulation Δt = time step
At the first time step, when t+Δt = 0, there is no information about the about the forces acting on the atoms or their velocities at time t. Therefore, the simulation is initialized with random set of velocities taken from a distribution based around the simulation’s temperature. The system must then be allowed to reach equilibration before the data can be used for analysis.
Ensembles
In a molecular dynamics simulation, the behavior of a fixed number of atoms is explored (constant N). Additional simulation conditions are also applied with respect to volume, pressure, and energy. There are three common ensembles that define these simulation conditions: NVE (constant number of atoms, volume, and energy), NVT (constant number of atoms, volume, and temperature) and NPT (constant number of atoms, pressure, and temperature). A variety of algorithms have been developed to enforce these conditions, such as the Andersen or Nosé-Hoover thermostats for controlling temperature. A researcher will choose an ensemble based on the questions they are trying to answer.6
Atomistic and Coarse-Grained Simulations
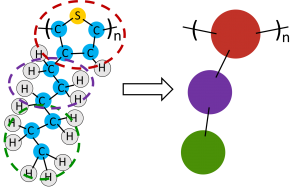
Depending on the time and length scales a researcher would like to explore, they may choose to use a coarse-grained force field. Instead of modeling each atom discretely, small clusters of atoms are grouped together into a single functional group and the interactions are approximated at a larger scale7, saving time in calculating interactions at every atomic site and allowing the simulation to reach larger lengths and times with reasonable computational expense. An example of coarse-graining a molecule is shown in Figure 2.
Figure 2. Poly(3-hexylthiophene) (P3HT) monomer for a coarse-grained molecular dynamics simulation. Clusters of atoms are turned into larger ‘beads’ with force field parameters representative of the large-scale collective behavior of the atoms or functional groups.
References
- A. Arbe, F. Alvarez and J. Colmenero, Neutron scattering and molecular dynamics simulations: synergetic tools to unravel structure and dynamics in polymers, Soft Matter, 2012, 8, 8257.
- J. N. Israelachvili, Intermolecular and Surface Forces, Elsevier Inc., 3rd ed., 2011.
- D. P. McMahon, D. L. Cheung, L. Goris, J. Dacuña, A. Salleo and A. Troisi, Relation between microstructure and charge transport in polymers of different regioregularity, J. Phys. Chem. C, 2011, 115, 19386–19393.
- P. C. Tapping, S. N. Clafton, K. N. Schwarz, T. W. Kee and D. M. Huang, Molecular-Level Details of Morphology-Dependent Exciton Migration in Poly(3-hexylthiophene) Nanostructures, J. Phys. Chem. C, 2015, 119, 7047–7059.
- M. Moreno, M. Casalegno, G. Raos, S. V. Meille and R. Po, Molecular Modeling of Crystalline Alkylthiophene Oligomers and Polymers, J. Phys. Chem. B, 2010, 114, 1591–1602.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, San Diego, 2nd edn., 2002.
- K. N. Schwarz, T. W. Kee and D. M. Huang, Coarse-grained simulations of the solution-phase self-assembly of poly(3-hexylthiophene) nanostructures, Nanoscale, 2013, 5, 2017.