Difference between revisions of "Fluorometer"
Cmditradmin (talk | contribs) m (→Significance) |
Cmditradmin (talk | contribs) m (→Significance) |
||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<table id="toc" style="width: 100%"> | |||
<tr> | |||
<td style="text-align: center; width: 33%">[[Main_Page#Research Equipment, Devices and Techniques|Return to Research Tool Menu]]</td> | |||
</tr> | |||
</table> | |||
=== Background === | === Background === | ||
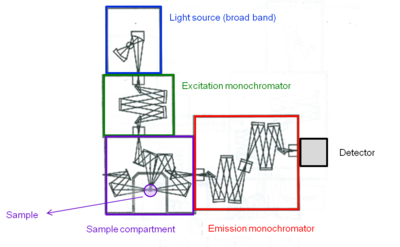
[[Image:Fluorometer_layout.png|thumb|400px|Internal layout of fluorometer components- Fluorolog-3, model FL3-12 (Horiba Jobin Yvon) ]] | |||
A fluorometer consists of an excitation monochromator which directs light of specific wavelength on a sample. A fluorescent sample produces and emission spectrum that is measured through a monochromator connected to a photomultiplier detector similar to spectrophotometer. | |||
=== Significance === | === Significance === | ||
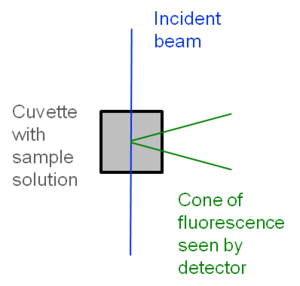
[[Image:Fluor_cuvette.png|thumb|300px|Excitation and fluorescence of sample in cuvette]] | |||
'''Fluorescence quantum yield determination using relavitive method''' | '''Fluorescence quantum yield determination using relavitive method''' | ||
One significant use of the fluorometer (or fluorimeter) is the determination of the fluorescence quantum yield. This is done using a relative method based on a reference compound of known quantum yield. The unknown sample and the reference sample are measured at the same excitation wavelengths and measurement conditions. The wavelength-integrated | One significant use of the fluorometer (or fluorimeter) is the determination of the fluorescence quantum yield. This is done using a relative method based on a reference compound of known quantum yield. The unknown sample and the reference sample are measured at the same excitation wavelengths and measurement conditions. The wavelength-integrated fluorescent intensity of both materials are then used in the calculation: | ||
:<math>\phi = \phi_{reference} \frac {F_{sample} / A_{sample}} {F_{reference}/ A_{reference}} \left( \frac {n_{sample}} {n_{reference}} \right) ^2\,\!</math> | :<math>\phi = \phi_{reference} \frac {F_{sample} / A_{sample}} {F_{reference}/ A_{reference}} \left( \frac {n_{sample}} {n_{reference}} \right) ^2\,\!</math> | ||
| Line 21: | Line 29: | ||
'''Optically dilute solution''' | '''Optically dilute solution''' | ||
The intensity of the excitation beam should be almost constant along excitation beam. The fluorescence signal is proportional to intensity of excitation beam and the intensity has to be the same for sample and reference. | |||
Typically: A ≤ 0.02 over 1 cm | Typically: A ≤ 0.02 over 1 cm path length | ||
From entrance face to center of cuvette: A = 0.01 | From entrance face to center of cuvette: A = 0.01 | ||
T= 10<sup>-A</sup> = 10<sup>-0.01</sup>= 0.977 | |||
How to proceed? | Therefore the intensity has changed only by 2% | ||
Measure A on higher concentration solution | |||
Dilute solution by (accurately) known factor | However, depending on absorption spectrometer used, measurement of A in this range may not be accurate enough. How to proceed? | ||
Perform fluorescence measurement on diluted solutions | *Measure A on higher concentration solution | ||
*Dilute solution by (accurately) known factor | |||
*Perform fluorescence measurement on diluted solutions | |||
'''Choice of excitation wavelength''' | '''Choice of excitation wavelength''' | ||
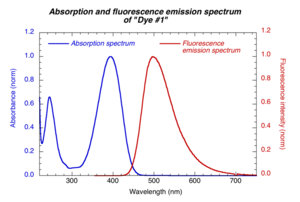
Excitation wavelength should be within the absorption band of the compounds | [[Image:Fluor_spectrum.png|thumb|300px| Excitation wavelength should be within the absorption band of the compounds | ||
]] | |||
The excitation wavelength should be within the absorption band of the compounds. The same excitation wavelength is used for reference and sample compounds. The emission spectrum is collected on the long wavelength side of the excitation wavelength (to avoid strong scattered light from excitation beam). | |||
In this test, we are using: λ<sub>exc</sub> = 350 nm | In this test, we are using: λ<sub>exc</sub> = 350 nm | ||
'''Repeated measurements''' | '''Repeated measurements''' | ||
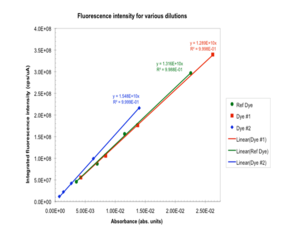
Deviations from linearity could indicate that emission was affected by reabsorption | Its always a good idea to have multiple data points! Prepare multiple dilutions and then measure fluorescence emission spectrum of each solution. Determine the slope of the line F/A for sample and reference. Deviations from linearity could indicate that emission was affected by reabsorption | ||
[[Image:Fluor_dilution.png|thumb|300px| Fluorescence intensity for various dilutions]] | |||
'''Reabsorption''' | '''Reabsorption''' | ||
Reabsorption is the absorption of the emitted light by the same solution before light exits cuvette. This is more significant for compounds with small Stokes shifts. Reabsorption can appear as a redshift (or decrease in fluorescence intensity on the short wavelength portion of the spectrum). The effect can be minimized by reducing concentration of solution. | |||
Reabsorption can appear as a redshift (or decrease in fluorescence intensity on the short wavelength portion of the spectrum) | <br clear='all'> | ||
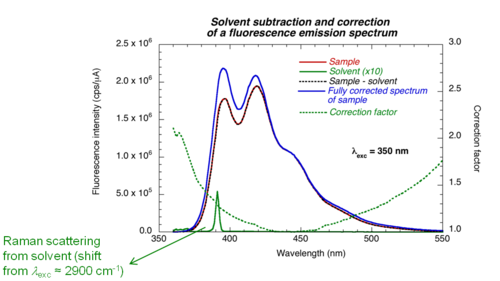
'''Corrected fluorescence spectra''' | '''Corrected fluorescence spectra''' | ||
Detectors and gratings do not have the same efficiency at all wavelengths | [[Image:Solvent_subtraction.png|thumb|500px| ]] | ||
Detectors and gratings do not have the same efficiency at all wavelengths. Therefore the results need to be corrected by a factor that accounts for wavelength response of the instrument. The contribution of the solvent (Raman scattering) and noise (dark counts) should also be subtracted. | |||
The contribution of the solvent (Raman scattering) and noise (dark counts) should also be subtracted | <br clear='all'> | ||
'''Sample Calculation''' | '''Sample Calculation''' | ||
F/A values n | F/A values n | ||
Sample (#1): 1.289 x | |||
Reference: 1.316 x | Sample (#1): 1.289 x 10<sup>10</sup> cps/mA 1.3288 (methanol) | ||
Reference: 1.316 x 10<sup>10</sup> cps/mA 1.4266 (cyclohexane) | |||
φ<sub>reference</sub> = 0.87) | φ<sub>reference</sub> = 0.87) | ||
:<math>\ | :<math>\phi_{sample} = \phi_{reference} \frac {F_{sample} / A_{sample}} {F_{reference}/ A_{reference}} \left( \frac {n_{sample}} {n_{reference}} \right) ^2\,\!</math> | ||
:<math>\ | :<math>\phi_{sample} = 0.87 * \frac {1.289} {1.316} * \left( \frac {1.3288} {1.4266} \right) ^2 = 8.87 * 0.979* 0.868= 0.74\,\!</math> | ||
=== Operation === | === Operation === | ||
{{#ev:youtube|5edJlvxcxrY}} | |||
=== External Links === | === External Links === | ||
[[Wikipedia:Fluorescence spectroscopy]] | [[Wikipedia:Fluorescence spectroscopy]] | ||
Latest revision as of 07:35, 12 October 2011
| Return to Research Tool Menu |
Background
A fluorometer consists of an excitation monochromator which directs light of specific wavelength on a sample. A fluorescent sample produces and emission spectrum that is measured through a monochromator connected to a photomultiplier detector similar to spectrophotometer.
Significance
Fluorescence quantum yield determination using relavitive method
One significant use of the fluorometer (or fluorimeter) is the determination of the fluorescence quantum yield. This is done using a relative method based on a reference compound of known quantum yield. The unknown sample and the reference sample are measured at the same excitation wavelengths and measurement conditions. The wavelength-integrated fluorescent intensity of both materials are then used in the calculation:
- <math>\phi = \phi_{reference} \frac {F_{sample} / A_{sample}} {F_{reference}/ A_{reference}} \left( \frac {n_{sample}} {n_{reference}} \right) ^2\,\!</math>
where
φ is the quantum yield
F= integrated fluorescence intensity
A= absorbance at excitation wavelength
n= refractive index
Optically dilute solution
The intensity of the excitation beam should be almost constant along excitation beam. The fluorescence signal is proportional to intensity of excitation beam and the intensity has to be the same for sample and reference.
Typically: A ≤ 0.02 over 1 cm path length
From entrance face to center of cuvette: A = 0.01
T= 10-A = 10-0.01= 0.977
Therefore the intensity has changed only by 2%
However, depending on absorption spectrometer used, measurement of A in this range may not be accurate enough. How to proceed?
- Measure A on higher concentration solution
- Dilute solution by (accurately) known factor
- Perform fluorescence measurement on diluted solutions
Choice of excitation wavelength
The excitation wavelength should be within the absorption band of the compounds. The same excitation wavelength is used for reference and sample compounds. The emission spectrum is collected on the long wavelength side of the excitation wavelength (to avoid strong scattered light from excitation beam).
In this test, we are using: λexc = 350 nm
Repeated measurements
Its always a good idea to have multiple data points! Prepare multiple dilutions and then measure fluorescence emission spectrum of each solution. Determine the slope of the line F/A for sample and reference. Deviations from linearity could indicate that emission was affected by reabsorption
Reabsorption
Reabsorption is the absorption of the emitted light by the same solution before light exits cuvette. This is more significant for compounds with small Stokes shifts. Reabsorption can appear as a redshift (or decrease in fluorescence intensity on the short wavelength portion of the spectrum). The effect can be minimized by reducing concentration of solution.
Corrected fluorescence spectra
Detectors and gratings do not have the same efficiency at all wavelengths. Therefore the results need to be corrected by a factor that accounts for wavelength response of the instrument. The contribution of the solvent (Raman scattering) and noise (dark counts) should also be subtracted.
Sample Calculation
F/A values n
Sample (#1): 1.289 x 1010 cps/mA 1.3288 (methanol)
Reference: 1.316 x 1010 cps/mA 1.4266 (cyclohexane)
φreference = 0.87)
- <math>\phi_{sample} = \phi_{reference} \frac {F_{sample} / A_{sample}} {F_{reference}/ A_{reference}} \left( \frac {n_{sample}} {n_{reference}} \right) ^2\,\!</math>
- <math>\phi_{sample} = 0.87 * \frac {1.289} {1.316} * \left( \frac {1.3288} {1.4266} \right) ^2 = 8.87 * 0.979* 0.868= 0.74\,\!</math>