Difference between revisions of "Hyper Rayleigh Scattering"
(New page: Hyper Rayleigh Scattering (aka Harmonic Light Scattering) is one method for measuring β. thumb|300px|The Hyper Rayleigh Scattering - Test best schematic An incide...) |
Cmditradmin (talk | contribs) m (→Technique) |
||
| (36 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<table id="toc" style="width: 100%"> | |||
<tr> | |||
<td style="text-align: center; width: 33%">[[Main_Page#Research Equipment, Devices and Techniques|Return to Research Tool Menu]]</td> | |||
</tr> | |||
</table> | |||
Hyper Rayleigh Scattering (aka Harmonic Light Scattering or HRS) is one method for measuring the [[first hyperpolarizability]] β. | |||
=== Overview === | |||
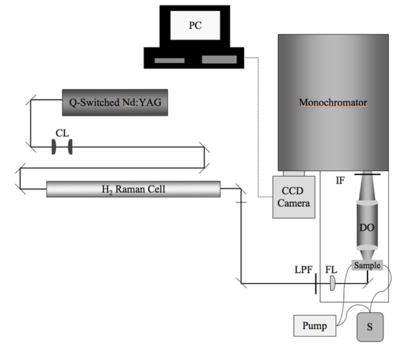
: | [[Image:Hrs.png|thumb|400px|Schematic of the HRS setup. CL = collimating lenses; LPF = long-pass filter; FL = 300-mm focusing lens; S = solution of chromophore in solvent of choice; DO = detection optics; IF = interference filter (950 nm)]] | ||
In HRS A dilute sample of a test chromophore is prepared in a solvent. An incident laser generates a second harmonic signal, specifically the frequency double signal from excitation of the sample molecules. This can be related to the beta of the sample using this formula: | |||
:<math>I^ {2 \omega }_{HRS} = [ (I ^ \omega_0 \cdot T ^ \omega_{solv})^2 G ] ( N_{solv} \langle \beta ^ 2 _{solv} \rangle + N_{sam} \langle \beta ^ 2 _{sam} \rangle ) \,\!</math> | |||
where | |||
:<math>I ^ \omega_0\,\!</math> is the intensity of the incident field | |||
:<math>T ^ \omega_{solv}\,\!</math> is the transmission of the fundamental radiation for the solvent | |||
:<math>G\,\!</math> is the instrumental efficiency | |||
:<math>N\,\!</math> is the number density of the sample (sam)and solvent (solv) | |||
:<math>\beta^2\,\!</math> is the orientational average of the square of the first hyperpolarizability. | |||
See Clays 1992 <ref>Clays, K.; Persoons, A., Hyper-Rayleigh scattering in solution. Rev. Sci. Instrum. 1992, 63 (6), 3285-9.</ref>. | |||
and Goovaerts 2001 <ref>Goovaerts, E.; Wenseleers, W. E.; Garcia, M. H.; Cross, G. H., Design and characterization of organic and organometallic molecules for second order nonlinear optics. Handbook of Advanced Electronic and Photonic Materials and Devices 2001, 9, 127-191</ref> | |||
There are a number of ways the HRS characterization method is used in non-linear optics research. | |||
The dielectric properties of the solvent influence the β (solvatochromatism). One area of research involves predicting and solvent effects so as to better understand the performance of molecules when densely packed in materials. Attempts have been made to calibrate HRS measurements with [[Electric-field induced second-harmonic generation | EFISH]] measurements of beta though they are based on different tensor elements. | |||
See Wikipedia on [http://en.wikipedia.org/wiki/Rayleigh_scattering Rayleigh Scattering] | |||
See also [[Density Functional Theory]] | See also [[Density Functional Theory]] | ||
See Wikipedia on [http://en.wikipedia.org/wiki/Raman_scattering Raman Scattering] | |||
<br clear='all'> | |||
=== Technique === | |||
The HRS measurement of β is a specialized device custom-built on an optics table. A series of mirrors, filters and devices [[hydrogen raman cell]] pass a specific wavelength of light into a sample which then emits light that is selected by a [[monochromator]] and then detected with a photocell. The components and configuration can change significantly from site to site. It is important to understand the significance of each portion of the setup. One possible HRS experimental setup is described here. (Press > to Play the video) | |||
<swf width="550" height="430">http://depts.washington.edu/cmditr/media/rayleigh.swf</swf> | |||
YouTube version: | |||
{{#ev:youtube|IP1HH6giIZU}} | |||
Low intensity background due to two-photon excited fluorescence can be fitted to a fourth order polynomial and subtracted. | |||
At this point a number of mathematical manipulations and comparisons can be done, for example comparing the sample HRS to a known reference sample with known beta, or internal referencing of the solvent contribution of beta. | |||
=== Significance === | |||
<br clear='all'> | |||
=== References=== | |||
<references/> | |||
<br clear='all'> | <br clear='all'> | ||
[[category:Research equipment]] | |||
Latest revision as of 09:22, 28 June 2010
| Return to Research Tool Menu |
Hyper Rayleigh Scattering (aka Harmonic Light Scattering or HRS) is one method for measuring the first hyperpolarizability β.
Overview
In HRS A dilute sample of a test chromophore is prepared in a solvent. An incident laser generates a second harmonic signal, specifically the frequency double signal from excitation of the sample molecules. This can be related to the beta of the sample using this formula:
- <math>I^ {2 \omega }_{HRS} = [ (I ^ \omega_0 \cdot T ^ \omega_{solv})^2 G ] ( N_{solv} \langle \beta ^ 2 _{solv} \rangle + N_{sam} \langle \beta ^ 2 _{sam} \rangle ) \,\!</math>
where
- <math>I ^ \omega_0\,\!</math> is the intensity of the incident field
- <math>T ^ \omega_{solv}\,\!</math> is the transmission of the fundamental radiation for the solvent
- <math>G\,\!</math> is the instrumental efficiency
- <math>N\,\!</math> is the number density of the sample (sam)and solvent (solv)
- <math>\beta^2\,\!</math> is the orientational average of the square of the first hyperpolarizability.
See Clays 1992 [1].
and Goovaerts 2001 [2]
There are a number of ways the HRS characterization method is used in non-linear optics research.
The dielectric properties of the solvent influence the β (solvatochromatism). One area of research involves predicting and solvent effects so as to better understand the performance of molecules when densely packed in materials. Attempts have been made to calibrate HRS measurements with EFISH measurements of beta though they are based on different tensor elements.
See Wikipedia on Rayleigh Scattering
See also Density Functional Theory
See Wikipedia on Raman Scattering
Technique
The HRS measurement of β is a specialized device custom-built on an optics table. A series of mirrors, filters and devices hydrogen raman cell pass a specific wavelength of light into a sample which then emits light that is selected by a monochromator and then detected with a photocell. The components and configuration can change significantly from site to site. It is important to understand the significance of each portion of the setup. One possible HRS experimental setup is described here. (Press > to Play the video)
<swf width="550" height="430">http://depts.washington.edu/cmditr/media/rayleigh.swf</swf>
YouTube version:
Low intensity background due to two-photon excited fluorescence can be fitted to a fourth order polynomial and subtracted.
At this point a number of mathematical manipulations and comparisons can be done, for example comparing the sample HRS to a known reference sample with known beta, or internal referencing of the solvent contribution of beta.
Significance
References
- ↑ Clays, K.; Persoons, A., Hyper-Rayleigh scattering in solution. Rev. Sci. Instrum. 1992, 63 (6), 3285-9.
- ↑ Goovaerts, E.; Wenseleers, W. E.; Garcia, M. H.; Cross, G. H., Design and characterization of organic and organometallic molecules for second order nonlinear optics. Handbook of Advanced Electronic and Photonic Materials and Devices 2001, 9, 127-191