Difference between revisions of "Model Calculations of Electronic Coupling"

From CleanEnergyWIKI
Jump to navigation Jump to search
 
(35 intermediate revisions by the same user not shown)
Line 3: Line 3:
<td style="text-align: left; width: 33%">[[Electronic Coupling|Previous Topic]]</td>
<td style="text-align: left; width: 33%">[[Electronic Coupling|Previous Topic]]</td>
<td style="text-align: center; width: 33%">[[Main_Page#Transport Properties|Return to Transport Properties Menu]]</td>
<td style="text-align: center; width: 33%">[[Main_Page#Transport Properties|Return to Transport Properties Menu]]</td>
<td style="text-align: right; width: 33%">[[Small Electronic Couplings and Marcus Theory| Next Topic]]</td>
<td style="text-align: right; width: 33%">[[Marcus Theory and Reorganization Energy| Next Topic]]</td>
</tr>
</tr>
</table>
</table>


There have not been that many measurements electronic coupling in pure perfect single crystal. Calculations based on wave function can predict the degree of electronic coupling for molecules at certain orientations. Researchers at Stuttgart have characterized oligo- acene single crystals.  This clearly shows band regime at low temperature with mobility decreasing with increasing temperature, then eventually a cross over localization and transition to a hopping regime, followed by a increasing mobility.


== Model calculations of electronic coupling ==
== HOMO and LUMO Level splitting ==


 
As two molecules come together there is an interaction resulting in the splitting of the HOMO an LUMO levels.
There have not been that many measurements of pure perfect single crystal. Researchers at Stuttgart have characterized oligo- acene single crystals.  This clearly shows band regime at low temperature with mobility decreasing with increasing temperature, then eventually a cross over localization and transition to a hopping regime, followed by a increasing mobility.
 
As you bring two molecules together there is an interaction resulting in the splitting of the HOMO an LUMO levels.


splitting HOMO ≡ 2 tHOMO  
splitting HOMO ≡ 2 tHOMO  
Line 25: Line 23:
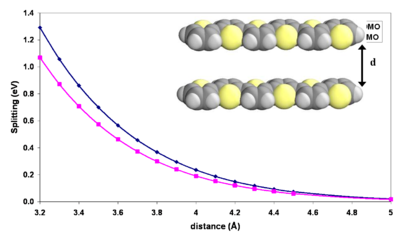
[[Image:Intermolecular_distance.png|thumb|400px|A bandgap appears as identical molecules approach each other perfectly cofacially. ]]
[[Image:Intermolecular_distance.png|thumb|400px|A bandgap appears as identical molecules approach each other perfectly cofacially. ]]


As the molecules come closer together their wavefunction overlap grows exponentially.
As the molecules come closer together their wave function overlap grows exponentially.


The exponential increase in energy with decreasing distance between the molecules is a manifestation that the splitting is caused by a wavefunction overlap. In the typical solid state intermolecular distances of 3.4 - 3.8 Å given a perfectly symmetrical, cofacial arrangement, there is splitting on the order of several tenths of an eV meaning a bandgap on the order of 1 eV. This consistent with formation of a band regime.  
The exponential increase in energy with decreasing distance between the molecules is a manifestation that the splitting is caused by a wave function overlap. In the typical solid state intermolecular distances of 3.4 - 3.8 Å given a perfectly symmetrical, cofacial arrangement, there is splitting on the order of several tenths of an eV meaning a bandgap on the order of 1 eV. This consistent with formation of a band regime.  


When molecules like this superimpose they do not line up directly above each other because areas of maximum density will align and repel. Instead they will slide a slight amount along the long and or short axis in order to adopt a packing mode that is more favorable. Halocyclophane molecules are hooked to each because of short alkyl chains that placed on the ends. This allows a cofacial configuration.
When molecules like this superimpose they do not line up directly above each other because areas of maximum density will align and repel. Instead they will slide a slight amount along the long and/or short axis in order to adopt a packing mode that is more favorable. Halocyclophane molecules are hooked to each because of the short alkyl chains on the ends. This allows a cofacial configuration.


As the molecules approach each other there will be displacement along the long axis and the bandgap between HOMO an LUMO will change.
As the molecules approach each other there will be displacement along the long axis and the bandgap between HOMO an LUMO will change.
Line 35: Line 33:
=== Influence of lateral displacements ===
=== Influence of lateral displacements ===


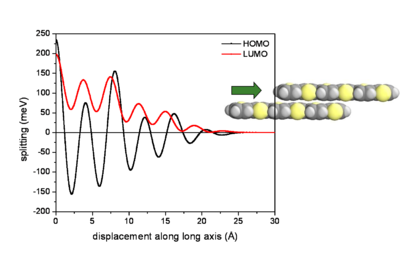
[[Image:Lateral_displacements.png|thumb|300px|Major fluctuations in bandwidths depending on the
[[Image:Lateral_displacements.png|thumb|400px|Major fluctuations in bandwidths depending on the
bonding/antibonding patterns of the HOMO/LUMO wavefunctions
bonding/antibonding patterns of the HOMO/LUMO wave functions
]]
]]
At an intermolecular distance of 4 Å  there will be an evolution of HOMO and LUMO according to the displacement of the two molecules. The graph begins with the gap of .2 and .25eV seen from the previous graph. The HOMO and LUMO have pronounced oscillations with increasing displacement. Notice that the level for HOMO goes from positive to negative passing through a zero where the electronic coupling and bandwidth for HOMO would be zero. The LUMO goes up and down but always has at least some bandwidth.
At an intermolecular distance of 4 Å  there will be an evolution of HOMO and LUMO according to the displacement of the two molecules. The graph begins with the gap of .2 and .25eV seen from the previous graph. The HOMO and LUMO have pronounced oscillations with increasing displacement. Notice that the level for HOMO goes from positive to negative passing through a zero where the electronic coupling and bandwidth for HOMO would be zero. The LUMO goes up and down but always has at least some bandwidth.
<br clear='all'>


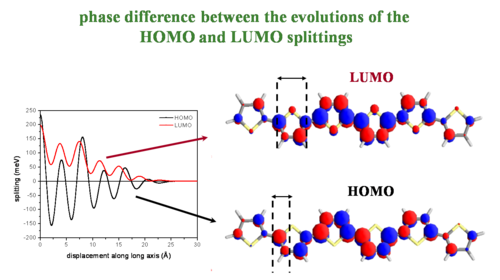
=== Phase difference between the evolutions of the HOMO and LUMO splittings ===
=== Phase difference between the evolutions of the HOMO and LUMO splittings ===
[[Image:Phase_homo_lumo.png|thumb|500px| The diagram of polythiophene (PT) shows the bonding factor for the double bond at beta carbons in the HOMO and the antibonding  factor at the single bond between the carbons (beneath the yellow sulfur) and between the rings.]]
Major fluctuations in bandwidths depend on the bonding/antibonding patterns of the HOMO/LUMO wave functions (the valence band and conduction bands). The diagram of polythiophene (PT) shows the bonding factor for the double bond at beta carbons in the HOMO and the antibonding factor at the single bond between the carbons (beneath the yellow sulfur) and between the rings.


[[Image:Phase_homo_lumo.png|thumb|300px| The diagram of polythiophene (PT) shows the bonding factor for the double bond at beta carbons in the HOMO and the antibonding  factor at the single bond between the carbons (beneath the yellow sulfur) and between the rings.]]
Two molecules that are perfectly aligned have each positive lobe on the bottom molecule aligning with the positive lobe on the top molecule.
Major fluctuations in bandwidths depend on the bonding/antibonding patterns of the HOMO/LUMO wavefunctions (the valence band and conduction bands). The diagram of polythiophene (PT) shows the bonding factor for the double bond at beta carbons in the HOMO and the antibonding  factor at the single bond between the carbons (beneath the yellow sulfur) and between the rings.  


Two molecules that are perfectly aligned have each positive lobe on the bottom molecule aligning with the positive lobe on the top molecule.
As two LUMO molecules slide past each other the sign stays the same but the degree of overlap alternates with each shift. This results in the always positive fluctuating line in the graph. As the molecules slide off each other they have fewer rings that interact and the total splitting energy is less.


If you slide two LUMO  molecules past each other the sign stays the same but the degree of overlap alternates with each shift. This results in the always positive fluctuating line in the graph. As the molecules slide off each other they have fewer rings that interact and the total splitting energy is less.
As the HOMO molecules slide by half a ring the positive MO overlaps with a negative resulting in a negative splitting, a full ring displacement gives a positive with a positive and so on. Again the total bandgap steadily decreases as the molecules slide off each other and have few interacting MOs.  


If you slide the HOMO molecules by half a ring the positive MO overlaps with a negative resulting in a negative splitting, a full ring displacement gives a positive with a positive and so on. Again the total bandgap steadily decreases as the molecules slide off each other and have few interacting MOs.  
As molecules displace against each other there will be large variations in the overlap, and therefore changes in the electronic coupling. The HOMO and LUMO patterns are completely different and depend on their bonding and antibonding patterns.


So as you displace molecules against each other there will be large variations in the overlap, and therefore changes in the electronic coupling. The HOMO and LUMO patterns are completely different and depend on their bonding and antibonding patterns.
<br clear='all'>


=== Influence of lateral displacements along short axis ===
=== Influence of lateral displacements along short axis ===
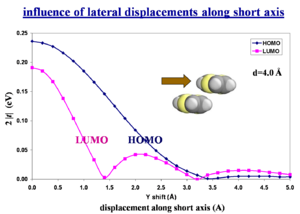
[[Image:Lateral_displacement_bandsplit.png|thumb|300px|This graph shows the influence of lateral displacements along short axis which show large variations between HOMO an LUMO.]]
[[Image:Lateral_displacement_bandsplit.png|thumb|300px|This graph shows the influence of lateral displacements along short axis which show large variations between HOMO an LUMO.]]


 
The wave function overlap is what matters, NOT the spatial overlap. The bonding-antibonding pattern of the HOMO or LUMO wave function is the critical factor. Quantum-chemistry calculations are required to predict this.  
What counts is the wavefunction overlap NOT the spatial overlap. The bonding-antibonding pattern of the HOMO or LUMO wavefunction is the critical factor.  
 
Quantum-chemistry calculations are required to predict this.  


Molecular motions / vibrations have a major impact because they result in small movements which change the overlap.
Molecular motions / vibrations have a major impact because they result in small movements which change the overlap.


Electron (conduction) bands can be intrinsically just as wide as hole (valence) bands. A misconception is that hole band must be narrower because of the number of nodes in antibonding orbitals in the LUMO. This logic doesn’t take into account overlap and displacements.
Electron (conduction) bands can be intrinsically just as wide as hole (valence) bands. A misconception is that hole band must be narrower because of the number of nodes in antibonding orbitals in the LUMO. This logic doesn’t take into account overlap and displacements.
<br clear='all'>
<br clear='all'>


Line 69: Line 67:


[[Image:Oligoacenes.png|thumb|200px|Oligoacenes with 1 to 5 rings]]
[[Image:Oligoacenes.png|thumb|200px|Oligoacenes with 1 to 5 rings]]
There is much current interest in oligoacenes. This goes back to the 1960s with interest in crystals of napthalene and anthracene for transport. Pentacene is still being studied by many groups because it has room temperature mobilities of 5 cm2/Vs for the holes. There is no practical use for oligoacenes longer than 5 rings because they too unstable and too hard to synthesize.
There is much current interest in oligoacenes. This goes back to the 1960s with interest in crystals of napthalene and anthracene for transport. Pentacene is still being studied by many groups because it has room temperature mobilities of 5 cm<sup>2</sup>/Vs for the holes. There is no practical use for oligoacenes longer than 5 rings because they too unstable and too hard to synthesize.
<br clear='all'>
<br clear='all'>




=== herringbone packing ===
=== Herringbone packing ===


[[Image:Herringbone_packing.png|thumb|400px|]]
[[Image:Herringbone_packing.png|thumb|400px|Herringbone packing showing major axes]]


The crystal packing of these molecules can be different from a simple cofacial situation. There is herringbone packing in which each layer is offset and molecules are stacked.
The crystal packing of these molecules can be different from a simple cofacial situation. There is herringbone packing in which each layer is offset and molecules are stacked.
Line 92: Line 90:
<br clear='all'>
<br clear='all'>


=== electronic couplings in pentacene ===
=== Bandwidth and electronic couplings in pentacene ===
The bandwidth varies depending on the orientaion of a crystal.
The bandwidth varies depending on the orientaion of a crystal. However there is a larger bandwidth if there was a stack built along the diagonal direction. Of course you can’t just build a one dimensional stack.


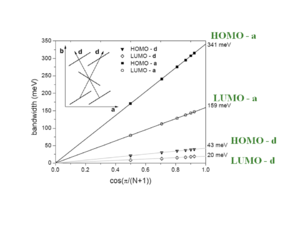
[[Image:Herringbone_packing_along_a.png|thumb|300px|left|In pentacene for a stack along the “a” direction  there is a bandwidth of .2 eV for both the HOMO and LUMO.]]
[[Image:Herringbone_packing_along_a.png|thumb|300px|left|In pentacene for a stack along the “a” direction  there is a bandwidth of .2 eV for both the HOMO and LUMO.]]


[[Image:Herringbone_packing_along_d.png|thumb|300px|However there is a larger bandwidth if there was a stack built along the diagonal direction. Of course you can’t just build a one dimensional stack.
[[Image:Herringbone_packing_along_d.png|thumb|300px|Bandwidth for pentacene stacked in the "d1" direction]]
]]
<br clear='all'>
<br clear='all'>
=== total bandwidths in oligoacenes ===


When you do three dimensional band structure calculations the bandwidths are pretty significant.  The figures noted here might be too big by a factor of 1.5 to 2 but even dividing by 2 they are still significant. At lower temperature you would get a better regime, this is the case with napthalene. The bandwidth are also large for the both for the electrons and the holes (HOMO and LUMO ). The bandwidth increases with chain length.  It is difficult to increase the length of these molecules, but it is possible to increase the width laterally to get a better bandwidth. These start to look like very small pieces of graphene; nanographene. Hexobenzochloraline forms disc- like molecules that are displaced to form a stacks and have a bandwidth of 1eV.
When you do three dimensional band structure calculations the bandwidths are pretty significant.  The figures noted here might be too big by a factor of 1.5 to 2 but even dividing by 2 they are still significant. At lower temperature you would get a better regime, this is the case with napthalene. The bandwidth are also large for the both for the electrons and the holes (HOMO and LUMO ). The bandwidth increases with chain length.  It is difficult to increase the length of these molecules, but it is possible to increase the width laterally to get a better bandwidth. These start to look like very small pieces of graphene; nanographene. Hexobenzochloraline forms disc- like molecules that are displaced to form a stacks and have a bandwidth of 1eV.
Line 116: Line 110:
|  napthalene
|  napthalene
|  0.43
|  0.43
|  0.47
|  0.37
|-
|-
|  anthracene
|  anthracene
Line 137: Line 131:


=== Pentacene band structure ===
=== Pentacene band structure ===
[[Image:Pentacene_bandstructure.png|thumb|400px|]]
[[Image:Pentacene_bandstructure.png|thumb|400px|Pentacene band structure as a function of orientation]]


These bandwidths would be accurate if all bands were perfect cosine type bands like you would have in a H&uuml;ckel treatment of applied binding approximation. But for example the crystal structure of pentacene there are two slightly nonequivalent molecules. There are two molecules per unit cell. As a result the valence and conduction bands are split into two sub-bands. The full bandwidth in each case is nearly the same, and the shape of HOMO and LUMO are also basically the same. However if we inject a hole it will go the top of the HOMO (marked in red on the figure to left) where there is a large dispersion. A large dispersion means there is a large coupling and therefore a high mobility. If you inject an electron it will go to the bottom of the conduction band (marked in red on the figure on the right) where the band is much flatter. If the band is flat it means the electronic coupling is lower and therefore the mobility is less. This shows that you should not look only at the total bandwidth, you also have to at the dispersion of the bands at the top of the valence band and the bottom of the conduction band because that is where the charge carriers will sit.
These bandwidths would be accurate if all bands were perfect cosine type bands like you would have in a H&uuml;ckel treatment of applied binding approximation. But for example the crystal structure of pentacene there are two slightly nonequivalent molecules. There are two molecules per unit cell. As a result the valence and conduction bands are split into two sub-bands. The full bandwidth in each case is nearly the same, and the shape of HOMO and LUMO are also basically the same. However if we inject a hole it will go the top of the HOMO (marked in red on the figure to left) where there is a large dispersion. A large dispersion means there is a large coupling and therefore a high mobility. If you inject an electron it will go to the bottom of the conduction band (marked in red on the figure on the right) where the band is much flatter. If the band is flat it means the electronic coupling is lower and therefore the mobility is less. This shows that you should not look only at the total bandwidth, you also have to at the dispersion of the bands at the top of the valence band and the bottom of the conduction band because that is where the charge carriers will sit.
Line 147: Line 141:
Rubrene is good illustration of the concepts presented earlier. Rubrene is a single crystal  for which has some of the best measurements have been made because it can be synthesized with few impurities leading to very large hole mobilities.  The four side phenyl rings move as far away from each other as possible because otherwise they would be cofacial at a distance that is very small, this distorts the bond connnecting the side rings to the tetracene. At first examination one might assume that rubrene would be a system that would not have large mobilities because the side phenyl rings would keep two adjacent molecules far apart. The larger the distance the between molecules, the less the overlap, and therefore the less the electronic coupling.  
Rubrene is good illustration of the concepts presented earlier. Rubrene is a single crystal  for which has some of the best measurements have been made because it can be synthesized with few impurities leading to very large hole mobilities.  The four side phenyl rings move as far away from each other as possible because otherwise they would be cofacial at a distance that is very small, this distorts the bond connnecting the side rings to the tetracene. At first examination one might assume that rubrene would be a system that would not have large mobilities because the side phenyl rings would keep two adjacent molecules far apart. The larger the distance the between molecules, the less the overlap, and therefore the less the electronic coupling.  


See Filho 2005 <ref>Filho et al., Adv. Mat. 17, 1072 (2005)</ref>
See Filho 2005 <ref name="filho">D. A. da Silva Filho,E.-G. Kim,J.-L. Brédas "Transport Properties in the Rubrene Crystal: Electronic Coupling and Vibrational Reorganization Energy" Adv. Mat. 17, 1072 (2005) {{Doi|10.1002/adma.200401866}} </ref>
<br clear='all'>
<br clear='all'>
[[Image:Rubrene_mobilities.png|thumb|300px|Charge mobility in rubrene vs temperatures]]
[[Image:Rubrene_mobilities.png|thumb|300px|Charge mobility and threshold voltage for in rubrene vs temperatures]]
 
[[Image:Rubrene_mobilities_3.png|thumb|300px|Electronic states near HOMO level]]


However this is not the case. Measurements by Podzorov at Rutgers has demonstrated that there is large mobility along the a axis of 20 cm2/Vs at room temperature. The graph also show that mobility increases with decreasing temperature down to 200 K which is consistent with a “band-like” regime. The mobility drops down again at very low temperature due to traps. If you warm up the system (up to 175K) there is enough energy for carriers to be detrapped.
However this is not the case. Measurements by Podzorov at Rutgers has demonstrated that there is large mobility along the a axis of 20 cm2/Vs at room temperature. The graph also show that mobility increases with decreasing temperature down to 200 K which is consistent with a “band-like” regime. The mobility drops down again at very low temperature due to traps. If you warm up the system (up to 175K) there is enough energy for carriers to be detrapped.
Line 167: Line 163:
<br clear='all'>
<br clear='all'>
[[Image:Bandwidth angle rubrene.png|thumb|300px|Bandwidths for rubrene along various orientations.]]
[[Image:Bandwidth angle rubrene.png|thumb|300px|Bandwidths for rubrene along various orientations.]]
see the [http://www.chemspider.com/ImageView.aspx?mode=3d&id=61510 Jmol visualization of rubrene]


The bandwidths along the “a” direction of the HOMO there is bandwidth of .35 eV which is very significant. This is because the molecules are displaced by 6.13 Å along the long axis, which means that there is only 1 .5 rings that are directly superimposed. On the other hand the distance between the two molecular planes is only 3.74 Å .
The bandwidths along the “a” direction of the HOMO there is bandwidth of .35 eV which is very significant. This is because the molecules are displaced by 6.13 Å along the long axis, which means that there is only 1 .5 rings that are directly superimposed. On the other hand the distance between the two molecular planes is only 3.74 Å .
<br clear='all'>
<br clear='all'>


[[Image:tetracene_displacement.png|thumb|300px|Transfer integral as a function of displacement of tetracene chains]]
[[Image:tetracene_displacement.png|thumb|300px|Transfer integral as a function of displacement of tetracene chains. See Filho 2005 <ref name="filho"/>]]
If you specify tetracene at distance of 3.74Å and displaced by 1.5 rings and then calculate the wave function you see oscillations in the HOMO and LUMO that roughly coincide with a transfer interval of .1 eV which leads to a bandwidth of .4 eV.  
If you specify tetracene at distance of 3.74Å and displaced by 1.5 rings and then calculate the wave function you see oscillations in the HOMO and LUMO that roughly coincide with a transfer interval of .1 eV which leads to a bandwidth of .4 eV.  


See Filho 2005 <ref>Filho et al., Adv. Mat. 17, 1072 (2005)</ref>
 
<br clear='all'>
<br clear='all'>
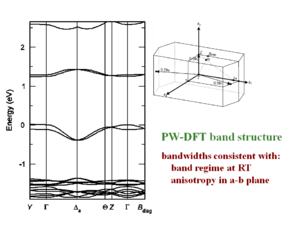
[[Image:3D_DFT_tetracene.png|thumb|300px|3D Density Functional Theory Bandstructure for ]]
[[Image:3D_DFT_tetracene.png|thumb|300px|Plane Wave Density Functional Theory Bandstructure]]


A three dimensional density functional theory band structure calculation results in a bandwidth of .35 eV.  This shows how you can explain mobilities by inferring the crystal structure based on a similar molecule with a known crystal structure. The crystal structure of fully rigid molecules is easier to predict; the rubrene side phenyl rings are “floppy” making its crystal structure difficult to predict.
A three dimensional density functional theory band structure calculation results in a bandwidth of .35 eV.  This shows how you can explain mobilities by inferring the crystal structure based on a similar molecule with a known crystal structure. The crystal structure of fully rigid molecules is easier to predict; the rubrene side phenyl rings are “floppy” making its crystal structure difficult to predict.
Line 187: Line 185:
<td style="text-align: left; width: 33%">[[Electronic Coupling|Previous Topic]]</td>
<td style="text-align: left; width: 33%">[[Electronic Coupling|Previous Topic]]</td>
<td style="text-align: center; width: 33%">[[Main_Page#Transport Properties|Return to Transport Properties Menu]]</td>
<td style="text-align: center; width: 33%">[[Main_Page#Transport Properties|Return to Transport Properties Menu]]</td>
<td style="text-align: right; width: 33%">[[Small Electronic Couplings and Marcus Theory| Next Topic]]</td>
<td style="text-align: right; width: 33%">[[Marcus Theory and Reorganization Energy| Next Topic]]</td>
</tr>
</tr>
</table>
</table>

Latest revision as of 09:04, 11 August 2010

Previous Topic Return to Transport Properties Menu Next Topic

There have not been that many measurements electronic coupling in pure perfect single crystal. Calculations based on wave function can predict the degree of electronic coupling for molecules at certain orientations. Researchers at Stuttgart have characterized oligo- acene single crystals. This clearly shows band regime at low temperature with mobility decreasing with increasing temperature, then eventually a cross over localization and transition to a hopping regime, followed by a increasing mobility.

HOMO and LUMO Level splitting

As two molecules come together there is an interaction resulting in the splitting of the HOMO an LUMO levels.

splitting HOMO ≡ 2 tHOMO in a 1D stack: HOMO = 4 HOMO = valence (hole) bandwidth

splitting LUMO ≡ 2 tLUMO in a 1D stack: LUMO = 4 LUMO = conduction (electron) bandwidth


Influence of intermolecular distance

A bandgap appears as identical molecules approach each other perfectly cofacially.

As the molecules come closer together their wave function overlap grows exponentially.

The exponential increase in energy with decreasing distance between the molecules is a manifestation that the splitting is caused by a wave function overlap. In the typical solid state intermolecular distances of 3.4 - 3.8 Å given a perfectly symmetrical, cofacial arrangement, there is splitting on the order of several tenths of an eV meaning a bandgap on the order of 1 eV. This consistent with formation of a band regime.

When molecules like this superimpose they do not line up directly above each other because areas of maximum density will align and repel. Instead they will slide a slight amount along the long and/or short axis in order to adopt a packing mode that is more favorable. Halocyclophane molecules are hooked to each because of the short alkyl chains on the ends. This allows a cofacial configuration.

As the molecules approach each other there will be displacement along the long axis and the bandgap between HOMO an LUMO will change.

Influence of lateral displacements

Major fluctuations in bandwidths depending on the bonding/antibonding patterns of the HOMO/LUMO wave functions

At an intermolecular distance of 4 Å there will be an evolution of HOMO and LUMO according to the displacement of the two molecules. The graph begins with the gap of .2 and .25eV seen from the previous graph. The HOMO and LUMO have pronounced oscillations with increasing displacement. Notice that the level for HOMO goes from positive to negative passing through a zero where the electronic coupling and bandwidth for HOMO would be zero. The LUMO goes up and down but always has at least some bandwidth.


Phase difference between the evolutions of the HOMO and LUMO splittings

The diagram of polythiophene (PT) shows the bonding factor for the double bond at beta carbons in the HOMO and the antibonding factor at the single bond between the carbons (beneath the yellow sulfur) and between the rings.

Major fluctuations in bandwidths depend on the bonding/antibonding patterns of the HOMO/LUMO wave functions (the valence band and conduction bands). The diagram of polythiophene (PT) shows the bonding factor for the double bond at beta carbons in the HOMO and the antibonding factor at the single bond between the carbons (beneath the yellow sulfur) and between the rings.

Two molecules that are perfectly aligned have each positive lobe on the bottom molecule aligning with the positive lobe on the top molecule.

As two LUMO molecules slide past each other the sign stays the same but the degree of overlap alternates with each shift. This results in the always positive fluctuating line in the graph. As the molecules slide off each other they have fewer rings that interact and the total splitting energy is less.

As the HOMO molecules slide by half a ring the positive MO overlaps with a negative resulting in a negative splitting, a full ring displacement gives a positive with a positive and so on. Again the total bandgap steadily decreases as the molecules slide off each other and have few interacting MOs.

As molecules displace against each other there will be large variations in the overlap, and therefore changes in the electronic coupling. The HOMO and LUMO patterns are completely different and depend on their bonding and antibonding patterns.


Influence of lateral displacements along short axis

This graph shows the influence of lateral displacements along short axis which show large variations between HOMO an LUMO.

The wave function overlap is what matters, NOT the spatial overlap. The bonding-antibonding pattern of the HOMO or LUMO wave function is the critical factor. Quantum-chemistry calculations are required to predict this.

Molecular motions / vibrations have a major impact because they result in small movements which change the overlap.

Electron (conduction) bands can be intrinsically just as wide as hole (valence) bands. A misconception is that hole band must be narrower because of the number of nodes in antibonding orbitals in the LUMO. This logic doesn’t take into account overlap and displacements.

Oligoacenes

Oligoacenes with 1 to 5 rings

There is much current interest in oligoacenes. This goes back to the 1960s with interest in crystals of napthalene and anthracene for transport. Pentacene is still being studied by many groups because it has room temperature mobilities of 5 cm2/Vs for the holes. There is no practical use for oligoacenes longer than 5 rings because they too unstable and too hard to synthesize.


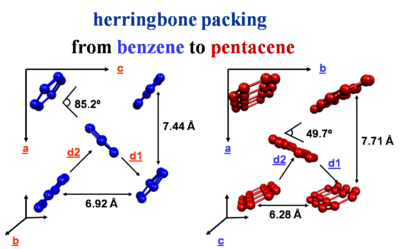
Herringbone packing

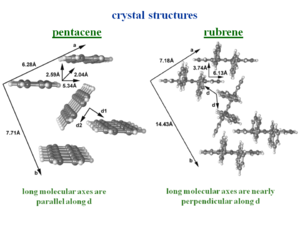
Herringbone packing showing major axes

The crystal packing of these molecules can be different from a simple cofacial situation. There is herringbone packing in which each layer is offset and molecules are stacked.

The strongest interactions are along the diagonal axis. Benzene has two layers of molecules within the unit cell. Whereas napthalene, anthracene, tetracene and pentacene have one layer per unit cell.

Much of the activity of transport occurs in the herringbone layers.

benzene: [1]

naphthalene: [2]

anthracene:  [3]

tetracene and pentacene: [4]

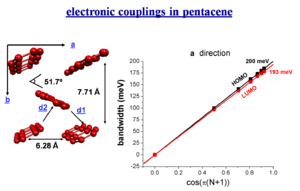
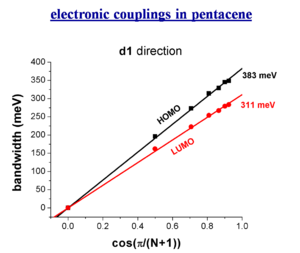
Bandwidth and electronic couplings in pentacene

The bandwidth varies depending on the orientaion of a crystal. However there is a larger bandwidth if there was a stack built along the diagonal direction. Of course you can’t just build a one dimensional stack.

In pentacene for a stack along the “a” direction there is a bandwidth of .2 eV for both the HOMO and LUMO.
Bandwidth for pentacene stacked in the "d1" direction


When you do three dimensional band structure calculations the bandwidths are pretty significant. The figures noted here might be too big by a factor of 1.5 to 2 but even dividing by 2 they are still significant. At lower temperature you would get a better regime, this is the case with napthalene. The bandwidth are also large for the both for the electrons and the holes (HOMO and LUMO ). The bandwidth increases with chain length. It is difficult to increase the length of these molecules, but it is possible to increase the width laterally to get a better bandwidth. These start to look like very small pieces of graphene; nanographene. Hexobenzochloraline forms disc- like molecules that are displaced to form a stacks and have a bandwidth of 1eV.

Total bandwidths in oligoacenes (in eV) from 3D tight-binding band-structure calculations

HOMO LUMO
napthalene 0.43 0.37
anthracene 0.54 0.48
tetacene 0.67 0.60
pentacene 0.72 0.70



See Cheng 2003 [5]

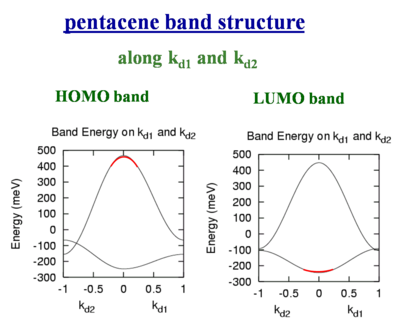
Pentacene band structure

Pentacene band structure as a function of orientation

These bandwidths would be accurate if all bands were perfect cosine type bands like you would have in a Hückel treatment of applied binding approximation. But for example the crystal structure of pentacene there are two slightly nonequivalent molecules. There are two molecules per unit cell. As a result the valence and conduction bands are split into two sub-bands. The full bandwidth in each case is nearly the same, and the shape of HOMO and LUMO are also basically the same. However if we inject a hole it will go the top of the HOMO (marked in red on the figure to left) where there is a large dispersion. A large dispersion means there is a large coupling and therefore a high mobility. If you inject an electron it will go to the bottom of the conduction band (marked in red on the figure on the right) where the band is much flatter. If the band is flat it means the electronic coupling is lower and therefore the mobility is less. This shows that you should not look only at the total bandwidth, you also have to at the dispersion of the bands at the top of the valence band and the bottom of the conduction band because that is where the charge carriers will sit.

Rubrene

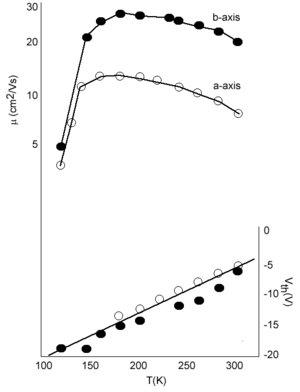
Rubrene is built on a tetracene backbone with four phenyl rings on the side that lie a in a plane that is perpendicular to the plane of the pentacene.

Rubrene is good illustration of the concepts presented earlier. Rubrene is a single crystal for which has some of the best measurements have been made because it can be synthesized with few impurities leading to very large hole mobilities. The four side phenyl rings move as far away from each other as possible because otherwise they would be cofacial at a distance that is very small, this distorts the bond connnecting the side rings to the tetracene. At first examination one might assume that rubrene would be a system that would not have large mobilities because the side phenyl rings would keep two adjacent molecules far apart. The larger the distance the between molecules, the less the overlap, and therefore the less the electronic coupling.

See Filho 2005 [6]

Charge mobility and threshold voltage for in rubrene vs temperatures
Electronic states near HOMO level

However this is not the case. Measurements by Podzorov at Rutgers has demonstrated that there is large mobility along the a axis of 20 cm2/Vs at room temperature. The graph also show that mobility increases with decreasing temperature down to 200 K which is consistent with a “band-like” regime. The mobility drops down again at very low temperature due to traps. If you warm up the system (up to 175K) there is enough energy for carriers to be detrapped.


See Podzorov 2004 [7]

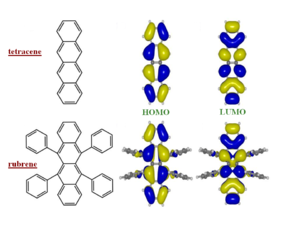
Tetracene

No π conjugation in rubrene side chains

From the point of view of the electronic structure one would not expect much difference from tetracene. The side phenyl rings are perpendicular to the pentacene backbone so π conjugation does not expand into them to a significant extent. Therefore the π conjugation is identical to pentacene. The game changes when you look at the crystal structure.

The side phenyl rings of rubrene change the nature of the herringbone packing pattern, twisting the second molecule of the unit cell.

The crystal structure tetracene is very similar to pentacene. The side phenyl rings of rubrene change the nature of the herringbone packing pattern, twisting the second molecule of the unit cell. The allows a unit stack to form along the “a” direction. This is where the largest mobilities have been measured.

Bandwidths for rubrene along various orientations.

see the Jmol visualization of rubrene

The bandwidths along the “a” direction of the HOMO there is bandwidth of .35 eV which is very significant. This is because the molecules are displaced by 6.13 Å along the long axis, which means that there is only 1 .5 rings that are directly superimposed. On the other hand the distance between the two molecular planes is only 3.74 Å .

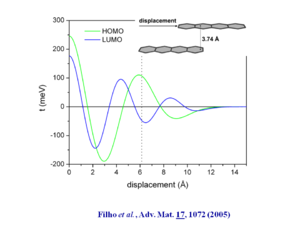
Transfer integral as a function of displacement of tetracene chains. See Filho 2005 [6]

If you specify tetracene at distance of 3.74Å and displaced by 1.5 rings and then calculate the wave function you see oscillations in the HOMO and LUMO that roughly coincide with a transfer interval of .1 eV which leads to a bandwidth of .4 eV.



Plane Wave Density Functional Theory Bandstructure

A three dimensional density functional theory band structure calculation results in a bandwidth of .35 eV. This shows how you can explain mobilities by inferring the crystal structure based on a similar molecule with a known crystal structure. The crystal structure of fully rigid molecules is easier to predict; the rubrene side phenyl rings are “floppy” making its crystal structure difficult to predict.

References

  1. ↑ G.E. Bacon et al. Proc. R. Soc. London Ser. A. 1964, 279, 98;
  2. ↑ V.I. Ponomarev et al. Kristallografiya, 1976, 21, 392;
  3. ↑ C. Pratt Brock et al. Acta Crystallogr., Sect. B (Str. Sci), 1990, 46, 795;
  4. ↑ D. Holmes et al. Chem. Eur. J. 1999, 5, 3399.
  5. ↑ Y.C. Cheng et al., J. Chem. Phys. 118, 3764 (2003)
  6. ↑ 6.0 6.1 D. A. da Silva Filho,E.-G. Kim,J.-L. Brédas "Transport Properties in the Rubrene Crystal: Electronic Coupling and Vibrational Reorganization Energy" Adv. Mat. 17, 1072 (2005) doi:10.1002/adma.200401866
  7. ↑ Podzorov et al., Phys. Rev. Lett. 93, 086602 (2004)
Previous Topic Return to Transport Properties Menu Next Topic
Retrieved from "http://cleanenergywiki.org/index.php?title=Model_Calculations_of_Electronic_Coupling&oldid=7703"