Difference between revisions of "Electronic Structure of Hydrogen"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| (15 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
<td style="text-align: left; width: 33%">[[Introduction|Previous Topic]]</td> | <td style="text-align: left; width: 33%">[[Introduction to Band Structure|Previous Topic]]</td> | ||
<td style="text-align: center; width: 33%">[[Main_Page#Electronic Band Structure of Organic Materials|Return to Band Structure Menu]]</td> | <td style="text-align: center; width: 33%">[[Main_Page#Electronic Band Structure of Organic Materials|Return to Band Structure Menu]]</td> | ||
<td style="text-align: right; width: 33%">[[The Polyene Series| Next Topic]]</td> | <td style="text-align: right; width: 33%">[[The Polyene Series| Next Topic]]</td> | ||
| Line 8: | Line 8: | ||
=== | === Electronic structure of hydrogen === | ||
[[Image:H2wavefunction.jpg|thumb|300px|Hydrogen | [[Image:H2wavefunction.jpg|thumb|300px|Hydrogen wave function]] | ||
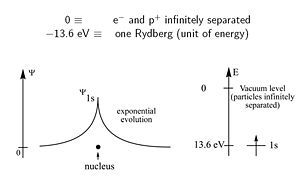
The hydrogen atom has | The hydrogen atom has a single electron and a proton. The atom holds together because of the coulombic attraction between the electron and the nucleus. That attraction leads to stabilization of the system of -13.6 ev (one Rydberg). This is how much energy it take to separate the proton from the electron. This does not happen at room temperature. The electron has a 1s atomic orbital. The wave function decreases as distance from the nucleus increases. The square of the wave function gives the probability of finding an electron. The wave function will not actually touch the nucleus but it will stay very close. | ||
When two hydrogen atoms approach one another: their ψ1s | When two hydrogen atoms approach one another: their ψ1s wave functions start overlapping and the 1s electrons start interacting. Molecular orbitals (MO) can be described using the atomic orbitals of the atoms forming the molecule. The hydrogen atom is the only element with an exact solution using Schrodingers equation. Even helium can not be solved exactly. The hydrogen molecule can be described using '''Linear Combination of Atomic Orbitals'''(LCAO). For n atomic orbitals you get n molecular orbitals. | ||
<br clear='all'> | <br clear='all'> | ||
=== Adding | === Adding wave functions === | ||
[[Image:h2wavecombined.JPG|thumb|300px|Hydrogen Molecular Orbital]] | [[Image:h2wavecombined.JPG|thumb|300px|Hydrogen Molecular Orbital]] | ||
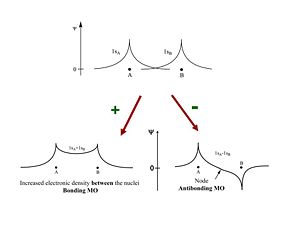
The two wave functions | The two wave functions 1S<sub>A</sub> and 1S<sub>B</sub> can be added constructively to produce a bonding orbital, or with opposite sign they add destructively to produce an antibonding molecular orbital. This describes the system quite well. The bonding orbital will have lower energy and create a more stable system. There has to be an increased density of electrons between the nuclei in order to form a molecule. The node in the antibonding MO decreases the density electrons and decreases the stability required to bring the two protons together. | ||
<br clear='all'> | <br clear='all'> | ||
| Line 25: | Line 25: | ||
[[Image:h2energelevels.JPG|thumb|300px|Energy levels for hydrogen electrons before and after bonding.]] | [[Image:h2energelevels.JPG|thumb|300px|Energy levels for hydrogen electrons before and after bonding.]] | ||
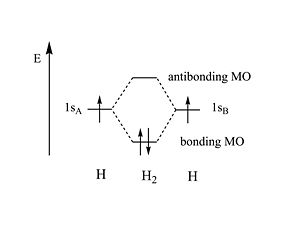
The energy of the bonding MO is lower than the energy of the two original atomic orbitals . If two electrons share the same | The energy of the bonding MO is lower than the energy of the two original atomic orbitals. If two electrons share the same wave function they have to opposite spins. When 2 hydrogen atoms form from electrons and protons the energy is 27.4 eV. The energy of the hydrogen bond 4eV; far smaller than the atomic bond energy. | ||
=== External Links === | |||
*[[wikipedia:Linear_combination_of_atomic_orbitals_molecular_orbital_method]] | |||
*[[wikipedia:Huckel_method]] | |||
[[category:electronic band structure]] | |||
<br clear='all'> | |||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
<td style="text-align: left; width: 33%">[[Introduction|Previous Topic]]</td> | <td style="text-align: left; width: 33%">[[Introduction to Band Structure|Previous Topic]]</td> | ||
<td style="text-align: center; width: 33%">[[Main_Page#Electronic Band Structure of Organic Materials|Return to Band Structure Menu]]</td> | <td style="text-align: center; width: 33%">[[Main_Page#Electronic Band Structure of Organic Materials|Return to Band Structure Menu]]</td> | ||
<td style="text-align: right; width: 33%">[[The Polyene Series| Next Topic]]</td> | <td style="text-align: right; width: 33%">[[The Polyene Series| Next Topic]]</td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Latest revision as of 12:34, 10 August 2010
| Previous Topic | Return to Band Structure Menu | Next Topic |
Electronic structure of hydrogen
The hydrogen atom has a single electron and a proton. The atom holds together because of the coulombic attraction between the electron and the nucleus. That attraction leads to stabilization of the system of -13.6 ev (one Rydberg). This is how much energy it take to separate the proton from the electron. This does not happen at room temperature. The electron has a 1s atomic orbital. The wave function decreases as distance from the nucleus increases. The square of the wave function gives the probability of finding an electron. The wave function will not actually touch the nucleus but it will stay very close.
When two hydrogen atoms approach one another: their ψ1s wave functions start overlapping and the 1s electrons start interacting. Molecular orbitals (MO) can be described using the atomic orbitals of the atoms forming the molecule. The hydrogen atom is the only element with an exact solution using Schrodingers equation. Even helium can not be solved exactly. The hydrogen molecule can be described using Linear Combination of Atomic Orbitals(LCAO). For n atomic orbitals you get n molecular orbitals.
Adding wave functions
The two wave functions 1SA and 1SB can be added constructively to produce a bonding orbital, or with opposite sign they add destructively to produce an antibonding molecular orbital. This describes the system quite well. The bonding orbital will have lower energy and create a more stable system. There has to be an increased density of electrons between the nuclei in order to form a molecule. The node in the antibonding MO decreases the density electrons and decreases the stability required to bring the two protons together.
Bonding and antibonding
The energy of the bonding MO is lower than the energy of the two original atomic orbitals. If two electrons share the same wave function they have to opposite spins. When 2 hydrogen atoms form from electrons and protons the energy is 27.4 eV. The energy of the hydrogen bond 4eV; far smaller than the atomic bond energy.
External Links
| Previous Topic | Return to Band Structure Menu | Next Topic |