Difference between revisions of "Optical Fiber Waveguides"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) m |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 6: | Line 6: | ||
</tr> | </tr> | ||
</table> | </table> | ||
[[Image:Circular_dielect_wg.png|thumb|300px|]] | [[Image:Circular_dielect_wg.png|thumb|300px|Circular dielectric waveguide]] | ||
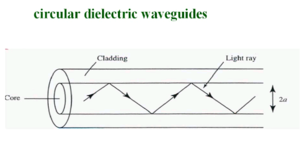
A circular dielectric waveguide or fiber optic has an internal core that has a higher index of refraction than the cladding. At a certain diameter there is an angle that is less than the critical angle so there is total internal reflection. | A circular dielectric waveguide or fiber optic has an internal core that has a higher index of refraction than the cladding. At a certain diameter there is an angle that is less than the critical angle so there is total internal reflection. | ||
[[Image:SI_fiber.png|thumb|300px|]] | [[Image:SI_fiber.png|thumb|300px|Step index fiber]] | ||
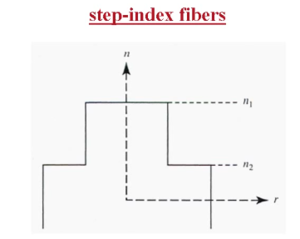
These are referred to as step index fibers. The y axis refers to the index of refraction. The x axis is the distance from the center of the core. So the highest index of refraction ( | These are referred to as step index fibers. The y axis refers to the index of refraction. The x axis is the distance from the center of the core. So the highest index of refraction (n<sub>1</sub>) is found in the core and there is a significant step in the index of refraction (n<sub>2</sub>) at the interface with the cladding. | ||
In most practical waveguides the refractive indices of the core and cladding differ from each other by only a few percent. | In most practical waveguides the refractive indices of the core and cladding differ from each other by only a few percent. | ||
The number of modes in a step-index circular waveguide is determined by the V parameter where | |||
:<math>\frac { | :<math>V= \frac {2\pi a} {\lambda_0} (n^2_1 - n^2_2)^{1/2}\,\!</math> | ||
where | |||
:<math>a\,\!</math> is the core radius | |||
:<math>n^ | :<math>(n^2_1 - n^2_2)^{1/2}\,\!</math> is referred to as the numerical aperature, the larger this term the larger the number of modes. | ||
The fiber can support only one mode when V < 2.405 | The fiber can support only one mode when V < 2.405 | ||
For | For n<sub>1</sub> = 1.48 and n<sub>2</sub> = 1.46, the radius of the core a <2.7μm | ||
[[Image:GI_fiber.png|thumb|300px|]] | <br clear='all'> | ||
[[Image:GI_fiber.png|thumb|300px|Graded index fiber]] | |||
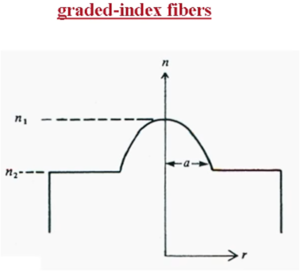
There is current research to develop a core with a graded index of refraction that gradually decreases to equal that of the cladding. This is referred to as a graded index fiber. | There is current research to develop a core with a graded index of refraction that gradually decreases to equal that of the cladding. This is referred to as a graded index fiber. | ||
<br clear='all'> | |||
[[category:Photonics applications]] | |||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
Latest revision as of 11:55, 29 December 2009
| Previous Topic | Return to Optical Fibers, Waveguides, and Lasers Menu | Next Topic |
A circular dielectric waveguide or fiber optic has an internal core that has a higher index of refraction than the cladding. At a certain diameter there is an angle that is less than the critical angle so there is total internal reflection.
These are referred to as step index fibers. The y axis refers to the index of refraction. The x axis is the distance from the center of the core. So the highest index of refraction (n1) is found in the core and there is a significant step in the index of refraction (n2) at the interface with the cladding.
In most practical waveguides the refractive indices of the core and cladding differ from each other by only a few percent.
The number of modes in a step-index circular waveguide is determined by the V parameter where
- <math>V= \frac {2\pi a} {\lambda_0} (n^2_1 - n^2_2)^{1/2}\,\!</math>
where
- <math>a\,\!</math> is the core radius
- <math>(n^2_1 - n^2_2)^{1/2}\,\!</math> is referred to as the numerical aperature, the larger this term the larger the number of modes.
The fiber can support only one mode when V < 2.405
For n1 = 1.48 and n2 = 1.46, the radius of the core a <2.7μm
There is current research to develop a core with a graded index of refraction that gradually decreases to equal that of the cladding. This is referred to as a graded index fiber.
| Previous Topic | Return to Optical Fibers, Waveguides, and Lasers Menu | Next Topic |