Difference between revisions of "Freederickz Transition and Dielectric Anisotropy"
Cmditradmin (talk | contribs) (New page: <table id="toc" style="width: 100%"> <tr> <td style="text-align: left; width: 33%">Previous Topic</td> <td style="text-align: center; width: 33%">[[Main_Page#Liquid Crystals...) |
Cmditradmin (talk | contribs) |
||
| (16 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
</tr> | </tr> | ||
</table> | </table> | ||
Applying an electric field to liquid crystal can change the orientation of molecules. | |||
=== Freedericksz Transition === | |||
[[Image:Electropolar.gif|thumb|Molecular dipoles orient in the presence of an electric field. This changes the index of refraction of the material.]] | |||
Recall that for materials that contain electric dipoles, such as water molecules, the dipoles themselves stretch or reorient in an applied field. | |||
If a dipole is at an angle to an electric field it will experience a torque that will rotate it into alignment. | |||
An electric field can also induce a polarization in a molecule (a polarizable molecule) along the long axis which will the cause it to align to the field even though it did not have a dipole to begin with. | |||
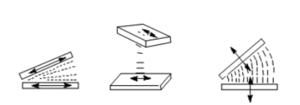
[[Image:Freedericksz.png|thumb|300px|An orthogonal electric field will align the director with the field]] | |||
A liquid crystal can be placed between two substrates that have been treated with polyimide so that the molecules are aligned homogeneously and in one direction. At the surface the liquid crystal molecules are influenced by interaction with the substrate. | |||
If then an electric field is applied orthogonal to this direction the liquid crystal will tend to rotate to align the director with the electric field assuming that the director and the dipole moment (more precisely the larger component of the dielectric anisotropy) are essentially co-linear. The reorientation starts in the middle where there is little surface interaction. | |||
This reorientation as depicted is called a Freedericksz transition. It should not be confused with a phase transition because the LC remains in the same LC phase. Simply, the orientation of the director is perturbed. The transition is smooth and is tunable by the amount of the electric field. | |||
Light that is polarized along the long axis will see anisotropic and birefringent material when the molecules are homogeneously aligned. When the molecules shift to be perpendicular to the substrate then light will see an isotropic surface. | |||
The optical properties of the material will be different depending on if they are homogeneously aligned or homotropically aligned. This can be changed by applying an electric field. It can be tuned by changing the surface alignment layer (pretilt angle). If the molecules are completely flat then a perpendicular electric field can not induce a polarization along the long axis. However if there some angle the field will induce some polarization along the long axis which will have some component that is perpendicular to the substrate. | |||
For an LCD application this polarization should be accomplished with a low voltage, it should occur very faster, and it should be stable over a large range of temperatures. This is not trivial because the forces working on the molecules at any one time may be unfavorable to one of these characteristics. | |||
=== Threshold voltage === | |||
[[Image:Splaytwistbend.png|thumb|300px|Splay (K<sub>11</sub>), Twist (K<sub>22</sub>) and Bend (K<sup>33</sup>)]] | |||
The threshold voltage (Vc) is the minimum voltage that will cause an LCD to switch. It depends on the square root of the on the elastic coefficient (K<sub>33</sub> and K<sub>22</sub>). The elastic coefficients refer to specific movements between molecules. The higher the elastic coefficients the harde it is to switch from one orientation to another. | |||
:<math>V_c = \pi \sqrt {\frac {K_{11} + ¼ (K_{33}-2 K_{22})} {\epsilon_0 \Delta \epsilon}}\,\!</math> | |||
Where: | |||
:<math>K_{11}\,\!</math> is the elastic coefficient for splaying | |||
:<math>K_{22}\,\!</math> is the elastic coefficient for twisting | |||
:<math>K_{33}\,\!</math> is the elastic coefficient for bending | |||
:<math>\epsilon_0\,\!</math> is the dielectric permittivity in free space | |||
:<math>\Delta \Epsilon\,\!</math> is the dielectric anisotropy of the system | |||
A uniaxial birefringent system has a dielectric constant along the axis and dielectric constant perpendicular to the long axis. The dielectric anisotropy relates to the difference between these two. If there is a dipole moment along the long axis it will make it very easy for the molecule to couple to the electric field and align. If there is no dipole moment but there is very large polarizability along the long axis then the field will induce a dipole, it will couple and then realign. So the two contributors to the dielectric constant are the susceptibility (polarizability for a material) and the dipole moment. A material with a high dielectric anisotropy has either a large dipole moment along the long axis and/or a large susceptibility. With no dielectric anisotropy there is nothing that will make it more stable to change orientation. | |||
It is good for the splay, twist and bend elastic coefficient to be relatively low. If they are too low then the liquid crystal will lose order with temperature. So there must be some balance between ease of polarization and stability. | |||
=== Anisotropic Nature of Polarizability === | |||
[[Image:Anis_polar.png|thumb|300px|An applied filed can induce a dipole in another direction]] | |||
In this example a field is applied along the long axis and there is large polarization. Applying a field perpendicular results in a very small polarization. If the molecule is oriented at an angle to the electric field and there is a high degree of polarizability along that axis and there is an oscillating electric field then the electrons will oscillate back and forth becoming a little antennae that will give off electromagnetic radiation. The polarization of the electromagnetic radiation has two components, one aligned along the axis of the applied field and a component along the perpendicular. If two polarizers are added and the molecule is located at an angle, then a dipole can be induced in the orthogonal direction which couples to the electric field and allows light to pass through. This induced polarization will be depend on the cosine of the angle. | |||
=== Summary === | |||
You now have all the ingredients to make a simple display; | |||
*You understand how liquid crystals align | |||
*You can control molecular alignment with surface alignment layers | |||
*Due to dielectric anisotropy we can force the molecule to change from parallel to the surface to perpendicular to the surface | |||
*Using a cross polarizer and depending on the how the molecules align, light can pass through or not. | |||
[[category:liquid crystals]] | |||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
Latest revision as of 13:58, 24 November 2009
| Previous Topic | Return to Liquid Crystal Menu | Next Topic |
Applying an electric field to liquid crystal can change the orientation of molecules.
Freedericksz Transition
Recall that for materials that contain electric dipoles, such as water molecules, the dipoles themselves stretch or reorient in an applied field.
If a dipole is at an angle to an electric field it will experience a torque that will rotate it into alignment.
An electric field can also induce a polarization in a molecule (a polarizable molecule) along the long axis which will the cause it to align to the field even though it did not have a dipole to begin with.
A liquid crystal can be placed between two substrates that have been treated with polyimide so that the molecules are aligned homogeneously and in one direction. At the surface the liquid crystal molecules are influenced by interaction with the substrate.
If then an electric field is applied orthogonal to this direction the liquid crystal will tend to rotate to align the director with the electric field assuming that the director and the dipole moment (more precisely the larger component of the dielectric anisotropy) are essentially co-linear. The reorientation starts in the middle where there is little surface interaction.
This reorientation as depicted is called a Freedericksz transition. It should not be confused with a phase transition because the LC remains in the same LC phase. Simply, the orientation of the director is perturbed. The transition is smooth and is tunable by the amount of the electric field.
Light that is polarized along the long axis will see anisotropic and birefringent material when the molecules are homogeneously aligned. When the molecules shift to be perpendicular to the substrate then light will see an isotropic surface.
The optical properties of the material will be different depending on if they are homogeneously aligned or homotropically aligned. This can be changed by applying an electric field. It can be tuned by changing the surface alignment layer (pretilt angle). If the molecules are completely flat then a perpendicular electric field can not induce a polarization along the long axis. However if there some angle the field will induce some polarization along the long axis which will have some component that is perpendicular to the substrate.
For an LCD application this polarization should be accomplished with a low voltage, it should occur very faster, and it should be stable over a large range of temperatures. This is not trivial because the forces working on the molecules at any one time may be unfavorable to one of these characteristics.
Threshold voltage
The threshold voltage (Vc) is the minimum voltage that will cause an LCD to switch. It depends on the square root of the on the elastic coefficient (K33 and K22). The elastic coefficients refer to specific movements between molecules. The higher the elastic coefficients the harde it is to switch from one orientation to another.
- <math>V_c = \pi \sqrt {\frac {K_{11} + ¼ (K_{33}-2 K_{22})} {\epsilon_0 \Delta \epsilon}}\,\!</math>
Where:
- <math>K_{11}\,\!</math> is the elastic coefficient for splaying
- <math>K_{22}\,\!</math> is the elastic coefficient for twisting
- <math>K_{33}\,\!</math> is the elastic coefficient for bending
- <math>\epsilon_0\,\!</math> is the dielectric permittivity in free space
- <math>\Delta \Epsilon\,\!</math> is the dielectric anisotropy of the system
A uniaxial birefringent system has a dielectric constant along the axis and dielectric constant perpendicular to the long axis. The dielectric anisotropy relates to the difference between these two. If there is a dipole moment along the long axis it will make it very easy for the molecule to couple to the electric field and align. If there is no dipole moment but there is very large polarizability along the long axis then the field will induce a dipole, it will couple and then realign. So the two contributors to the dielectric constant are the susceptibility (polarizability for a material) and the dipole moment. A material with a high dielectric anisotropy has either a large dipole moment along the long axis and/or a large susceptibility. With no dielectric anisotropy there is nothing that will make it more stable to change orientation.
It is good for the splay, twist and bend elastic coefficient to be relatively low. If they are too low then the liquid crystal will lose order with temperature. So there must be some balance between ease of polarization and stability.
Anisotropic Nature of Polarizability
In this example a field is applied along the long axis and there is large polarization. Applying a field perpendicular results in a very small polarization. If the molecule is oriented at an angle to the electric field and there is a high degree of polarizability along that axis and there is an oscillating electric field then the electrons will oscillate back and forth becoming a little antennae that will give off electromagnetic radiation. The polarization of the electromagnetic radiation has two components, one aligned along the axis of the applied field and a component along the perpendicular. If two polarizers are added and the molecule is located at an angle, then a dipole can be induced in the orthogonal direction which couples to the electric field and allows light to pass through. This induced polarization will be depend on the cosine of the angle.
Summary
You now have all the ingredients to make a simple display;
- You understand how liquid crystals align
- You can control molecular alignment with surface alignment layers
- Due to dielectric anisotropy we can force the molecule to change from parallel to the surface to perpendicular to the surface
- Using a cross polarizer and depending on the how the molecules align, light can pass through or not.
| Previous Topic | Return to Liquid Crystal Menu | Next Topic |