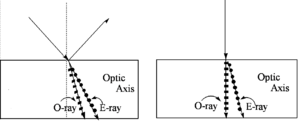Difference between revisions of "Double Refraction and Birefringence"
Cmditradmin (talk | contribs) (New page: <table id="toc" style="width: 100%"> <tr> <td style="text-align: left; width: 33%">Previous Topic</td> <td style="text-align: center; width: 33%">[[Main_Page#Liquid Cry...) |
Cmditradmin (talk | contribs) m |
||
| (14 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
<td style="text-align: left; width: 33%">[[Liquid Crystals|Previous Topic]]</td> | <td style="text-align: left; width: 33%">[[Liquid Crystals|Previous Topic]]</td> | ||
<td style="text-align: center; width: 33%">[[Main_Page#Liquid Crystals and Displays|Return to Liquid Crystal Menu]]</td> | <td style="text-align: center; width: 33%">[[Main_Page#Liquid Crystals and Displays|Return to Liquid Crystal Menu]]</td> | ||
<td style="text-align: right; width: 33%">[[ | <td style="text-align: right; width: 33%">[[Director – Degrees of Order in Liquid Crystals|Next Topic]]</td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Liquid crystals can effectively shutter light by rapidly changing the index of refraction. There are several basic optical principles that are needed to explain the phenomenon. | |||
=== Wave Surfaces === | |||
[[Image:Wavesurface.png|thumb|300px|An isotropic material with a larger index of refraction would have a smaller wave surface at any arbitrary time because light waves would propagate slower.]] | |||
There are two useful constructs when considering liquid crystals; wave surfaces and index elipsoids. | |||
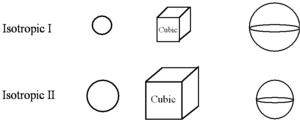
A material that an isotropic refractive index has the same index of refraction from all directions. An example is a crystal with a cubic lattice. | |||
The electric field of light is perpendicular to its direction of propagation. A point source emitting light from the center of an isotropic crystal emanates light outward uniformly in all directions. The position of the wave front defines a sphere (wave surface) whose radius is increasing with time | |||
Think about a point source in the center of the material emitting light that forms a wave surface. The wave surface is the tangent to the surface of the wavefront of a wave of light coming from that point. In a isotropic material the wave surface forms a sphere. In a material with a higher index of refraction the wave surface has a smaller radius. | |||
We can also draw another construct with a surface defined by a vector whose magnitude is the refractive index of light travelling in a given direction. In isotropic material this surface would also form a sphere, however since the magnitude of each vector is greater with a higher index of refraction this surface would have a large radius for when there is a higher index of refraction. In the example the first low index material has a larger wave surface than the second material which has a high index. | |||
If we chose another material with a larger susceptibility (more polarizable), its wave surface would expand more slowly because the susceptibility relates to the square of the refractive index. At an arbitrary time (t), the wave surface shows a radius inversely proportional to the index of refraction. | |||
=== Anisotropic Materials === | |||
[[Image:Anisotropic.png|thumb|300px|An anisotropic material has an ellipsoidal wave surface with respect to extraordinary waves which are polarized perpendicular to the optic axis. Ordinary waves polarized with the optic axis still see an isotropic material and the wave surface is spherical.]] | |||
In an anisotropic material the index of refraction is not the same for each direction. We ask for different polarizations of light what will the wave surface look like? | |||
For non-cubic single crystals, such as a hypothetical crystal of 2,4-hexadiyne, the index of refraction and, hence, the polarizability vary with the direction that the light travels through the crystal. | |||
The hypothetical crystal of 2,4-hexadiyne is uniaxial, where the unique axis is referred to as the optic axis. Light propagates along the optic access and polarization is perpendicular to the direction of propagation. Any direction perpendicular to that axis will have the same index of refraction. If light travels perpendicular to the long axis (eg light is polarized in a different direction) it encounters a lower index of refraction and its wave surface is smaller. | |||
For such a material: | |||
:<math>n_x = n_y \neq n_z\,\!</math> | |||
We can compare two surfaces. The ordinary wave surface (Sord) has a component of polarization that is not along the unique axis (z) of the molecule, that is polarized along Nx or Ny. The extraordinary wave surface (Sext) has a polarization that is oriented along the unique axis (z). This results in a different wave surface depending on the direction. This kind of materials is called birefringent. If you have light shining along the x or y axis travels more slowly resulting in double refraction. | |||
Other non-cubic crystals are characterized by two optical axes (i.e. there are three distinct axes) and are said to be optically biaxial. | |||
=== Double Refraction === | |||
[[Image:Calcite.jpg|thumb|300px|Here is an example of a crystal of calcite exhibiting double refringence or double refraction.]] | |||
When a beam of unpolarized light enters a birefringent crystal at normal incidence (but not along the optic axis), two light beams emerge. This effect (first observed in calcite by the Vikings) is called double refraction: | |||
One ray, which we call the ordinary ray, passes straight through the crystal. | |||
The other ray, called the extraordinary ray diverges as it passes through the crystal and becomes displaced. The relative polarization of the two emerging beams is orthogonal. | |||
Here is an example of a crystal of calcite. The ordinary ray is able to pass straight through the crystal. The second line is produced by the extraordinary beam. The extraordinary beam does not follow Schnell’s law which holds only for isotropic materials. | |||
If you place a cross polarizer over the crystal one or the other of the double refracted lines will disappear. They have orthogonal polarization. | |||
=== Birefringence === | |||
Christiaan Huygens (1629 - 1695), Dutch physicist first explained double refraction. | |||
We can describe a beam of unpolarized light as the superposition of two orthogonally polarized rays (electric fields at 90 degrees to each other) traversing the same path. | |||
When both rays encounter the same index of refraction, as in an isotropic medium, or when the direction of propagation occurs along an optic of an anisotropic crystal, axis (i.e. the light is polarized in a direction perpendicular to the optic axis)the beams remain collinear and in phase. | |||
For light polarized perpendicular to the optic axis, the material appears isotropic and the index of refraction is independent of the direction of propagation. We call this angularly independent index the ordinary index of refraction (no). | |||
If light is not polarized perpendicular to the optic axis, the index of refraction varies as a function of the direction of propagation. The angularly sensitive index becomes the extraordinary index of refraction (ne). | |||
The extraordinary beam encounter the maximum or minimum refraction depending on its angle, resulting in an index ellipsoid. In calcite the long axis has a higher index, while the perpendicular to the long axis has a smaller index. (The long axis not have to be the direction of maximum index). At the minimum value the extraordinary beam has an index that is the same as the ordinary beam. | |||
=== Double Refraction === | |||
[[Image:Doublerefract.png|thumb|300px|An extraordinary ray (E-ray) is polarized perpendicular to the optic axis and experiences a different index of refraction than the ordinary ray (O-ray) ]] | |||
One beam follows a normal path and the other will start to diverge. | |||
See the description on the Olympus Website <ref>http://www.olympusmicro.com/primer/lightandcolor/birefringenceintro.html</ref> | |||
For the extraordinary ray the little dots indicate the polarizatin is in and out of the plane. For the ordinary ray the | |||
little lines indicate the polarization is in the plane. If there light ray that is perpendicular to the optical axis the ordinary ray will pass straight through and the extraordinary beam will divert resulting in two beams of light. This bears on the behavior of light in liquid crystals. | |||
We can describe a beam of unpolarized light as the superposition of two orthogonally polarized rays (electric fields at 90 degrees to each other) traversing the same path. | |||
When both rays encounter the same index of refraction, as in an isotropic medium, or when the direction of propagation occurs along an optic axis of an anisotropic crystal, axis (i.e. the light is polarized in a direction perpendicular to the optic axis)the beams remain collinear and in phase. | |||
For light polarized perpendicular to the optic axis, the material appears isotropic and the index of refraction is independent of the direction of propagation. We call this angularly independent index the ordinary index of refraction n<sub>o</sub>. | |||
If light is not polarized perpendicular to the optic axis, the index of refraction varies as a function of the direction of propagation. The anglar sensitive index becomes the extraordinary index of refraction n<sub>e</sub> | |||
=== Explanation of double refraction === | |||
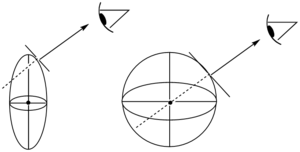
[[Image:Doublerefract_eye.png|thumb|300px|An ellipsoidal extraordinary wave surface on the left and a spherical ordinary wave surface on the right]] | |||
For light traveling through a birefringent material except along the optic axis, the two orthogonally polarized rays "see" different polarizabilities and thus, different refractive indices.You can think of it as wave surfaces. Light will leave the material in a direction that is perpendicular to the tangent of the wavesurface at the exit point. | |||
One ray becomes retarded relative to the other (introducing a phase shift) and diverges. | |||
A uniaxial material will therefore have two wave surfaces, a spherical ordinary wave surface and an ellipsoidal extraordinary wave surface. (Note that the magnitudes of the principal axes of the wave surface are inversely proportional to the refractive indices normal to the direction of propagation). | |||
Light rays propagate at normal incidence for a wave surface, and your eye traces that rays perceived origin within the wave surface. | |||
The origin of the extraordinary ray (unless the ray is traveling along or perpendicular to the optic axis) will appear displaced. | |||
However for the ordinary wave surface ray will be traced back to its real origin (if eminent from within the materials or strikes the material at a normal incidence) and pass through the center of the wave surface. | |||
=== References === | |||
<references/> | |||
[[category:liquid crystals]] | |||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
<td style="text-align: left; width: 33%">[[Liquid Crystals|Previous Topic]]</td> | <td style="text-align: left; width: 33%">[[Liquid Crystals|Previous Topic]]</td> | ||
<td style="text-align: center; width: 33%">[[Main_Page#Liquid Crystals and Displays|Return to Liquid Crystal Menu]]</td> | <td style="text-align: center; width: 33%">[[Main_Page#Liquid Crystals and Displays|Return to Liquid Crystal Menu]]</td> | ||
<td style="text-align: right; width: 33%">[[ | <td style="text-align: right; width: 33%">[[Director – Degrees of Order in Liquid Crystals|Next Topic]]</td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Latest revision as of 13:28, 2 September 2009
| Previous Topic | Return to Liquid Crystal Menu | Next Topic |
Liquid crystals can effectively shutter light by rapidly changing the index of refraction. There are several basic optical principles that are needed to explain the phenomenon.
Wave Surfaces
There are two useful constructs when considering liquid crystals; wave surfaces and index elipsoids.
A material that an isotropic refractive index has the same index of refraction from all directions. An example is a crystal with a cubic lattice. The electric field of light is perpendicular to its direction of propagation. A point source emitting light from the center of an isotropic crystal emanates light outward uniformly in all directions. The position of the wave front defines a sphere (wave surface) whose radius is increasing with time
Think about a point source in the center of the material emitting light that forms a wave surface. The wave surface is the tangent to the surface of the wavefront of a wave of light coming from that point. In a isotropic material the wave surface forms a sphere. In a material with a higher index of refraction the wave surface has a smaller radius.
We can also draw another construct with a surface defined by a vector whose magnitude is the refractive index of light travelling in a given direction. In isotropic material this surface would also form a sphere, however since the magnitude of each vector is greater with a higher index of refraction this surface would have a large radius for when there is a higher index of refraction. In the example the first low index material has a larger wave surface than the second material which has a high index.
If we chose another material with a larger susceptibility (more polarizable), its wave surface would expand more slowly because the susceptibility relates to the square of the refractive index. At an arbitrary time (t), the wave surface shows a radius inversely proportional to the index of refraction.
Anisotropic Materials
In an anisotropic material the index of refraction is not the same for each direction. We ask for different polarizations of light what will the wave surface look like?
For non-cubic single crystals, such as a hypothetical crystal of 2,4-hexadiyne, the index of refraction and, hence, the polarizability vary with the direction that the light travels through the crystal.
The hypothetical crystal of 2,4-hexadiyne is uniaxial, where the unique axis is referred to as the optic axis. Light propagates along the optic access and polarization is perpendicular to the direction of propagation. Any direction perpendicular to that axis will have the same index of refraction. If light travels perpendicular to the long axis (eg light is polarized in a different direction) it encounters a lower index of refraction and its wave surface is smaller.
For such a material:
- <math>n_x = n_y \neq n_z\,\!</math>
We can compare two surfaces. The ordinary wave surface (Sord) has a component of polarization that is not along the unique axis (z) of the molecule, that is polarized along Nx or Ny. The extraordinary wave surface (Sext) has a polarization that is oriented along the unique axis (z). This results in a different wave surface depending on the direction. This kind of materials is called birefringent. If you have light shining along the x or y axis travels more slowly resulting in double refraction.
Other non-cubic crystals are characterized by two optical axes (i.e. there are three distinct axes) and are said to be optically biaxial.
Double Refraction
When a beam of unpolarized light enters a birefringent crystal at normal incidence (but not along the optic axis), two light beams emerge. This effect (first observed in calcite by the Vikings) is called double refraction:
One ray, which we call the ordinary ray, passes straight through the crystal.
The other ray, called the extraordinary ray diverges as it passes through the crystal and becomes displaced. The relative polarization of the two emerging beams is orthogonal.
Here is an example of a crystal of calcite. The ordinary ray is able to pass straight through the crystal. The second line is produced by the extraordinary beam. The extraordinary beam does not follow Schnell’s law which holds only for isotropic materials.
If you place a cross polarizer over the crystal one or the other of the double refracted lines will disappear. They have orthogonal polarization.
Birefringence
Christiaan Huygens (1629 - 1695), Dutch physicist first explained double refraction.
We can describe a beam of unpolarized light as the superposition of two orthogonally polarized rays (electric fields at 90 degrees to each other) traversing the same path.
When both rays encounter the same index of refraction, as in an isotropic medium, or when the direction of propagation occurs along an optic of an anisotropic crystal, axis (i.e. the light is polarized in a direction perpendicular to the optic axis)the beams remain collinear and in phase.
For light polarized perpendicular to the optic axis, the material appears isotropic and the index of refraction is independent of the direction of propagation. We call this angularly independent index the ordinary index of refraction (no).
If light is not polarized perpendicular to the optic axis, the index of refraction varies as a function of the direction of propagation. The angularly sensitive index becomes the extraordinary index of refraction (ne).
The extraordinary beam encounter the maximum or minimum refraction depending on its angle, resulting in an index ellipsoid. In calcite the long axis has a higher index, while the perpendicular to the long axis has a smaller index. (The long axis not have to be the direction of maximum index). At the minimum value the extraordinary beam has an index that is the same as the ordinary beam.
Double Refraction
One beam follows a normal path and the other will start to diverge.
See the description on the Olympus Website [1]
For the extraordinary ray the little dots indicate the polarizatin is in and out of the plane. For the ordinary ray the little lines indicate the polarization is in the plane. If there light ray that is perpendicular to the optical axis the ordinary ray will pass straight through and the extraordinary beam will divert resulting in two beams of light. This bears on the behavior of light in liquid crystals.
We can describe a beam of unpolarized light as the superposition of two orthogonally polarized rays (electric fields at 90 degrees to each other) traversing the same path.
When both rays encounter the same index of refraction, as in an isotropic medium, or when the direction of propagation occurs along an optic axis of an anisotropic crystal, axis (i.e. the light is polarized in a direction perpendicular to the optic axis)the beams remain collinear and in phase.
For light polarized perpendicular to the optic axis, the material appears isotropic and the index of refraction is independent of the direction of propagation. We call this angularly independent index the ordinary index of refraction no.
If light is not polarized perpendicular to the optic axis, the index of refraction varies as a function of the direction of propagation. The anglar sensitive index becomes the extraordinary index of refraction ne
Explanation of double refraction
For light traveling through a birefringent material except along the optic axis, the two orthogonally polarized rays "see" different polarizabilities and thus, different refractive indices.You can think of it as wave surfaces. Light will leave the material in a direction that is perpendicular to the tangent of the wavesurface at the exit point.
One ray becomes retarded relative to the other (introducing a phase shift) and diverges. A uniaxial material will therefore have two wave surfaces, a spherical ordinary wave surface and an ellipsoidal extraordinary wave surface. (Note that the magnitudes of the principal axes of the wave surface are inversely proportional to the refractive indices normal to the direction of propagation).
Light rays propagate at normal incidence for a wave surface, and your eye traces that rays perceived origin within the wave surface. The origin of the extraordinary ray (unless the ray is traveling along or perpendicular to the optic axis) will appear displaced. However for the ordinary wave surface ray will be traced back to its real origin (if eminent from within the materials or strikes the material at a normal incidence) and pass through the center of the wave surface.
References
| Previous Topic | Return to Liquid Crystal Menu | Next Topic |