Difference between revisions of "Electron-Phonon Coupling"
Cmditradmin (talk | contribs) m |
|||
| (27 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
<td style="text-align: left; width: 33%">[[ | <td style="text-align: left; width: 33%">[[Marcus Theory and Reorganization Energy|Previous Topic]]</td> | ||
<td style="text-align: center; width: 33%">[[Main_Page#Transport Properties|Return to Transport Properties Menu]]</td> | <td style="text-align: center; width: 33%">[[Main_Page#Transport Properties|Return to Transport Properties Menu]]</td> | ||
| Line 7: | Line 7: | ||
</table> | </table> | ||
The frontier of research in organic semiconductors is attempting to get a complete picture of electron transport by understanding intramolecular and intermolecular vibrations or [[phonon | phonons]] and electron-phonon coupling. Several people have been working on this for a while. | |||
The frontier of research in organic semiconductors is attempting to get a complete picture of electron transport | |||
Silbey & Munn | Silbey & Munn | ||
Bobbert et al. | Bobbert et al. | ||
| Line 18: | Line 14: | ||
Shuai et al. | Shuai et al. | ||
=== Tight-binding Hamiltonian === | |||
[[Image:tight_hamiltonian.png|thumb|400px|Tight binding Hamilitonian expression]] | |||
This is the second quantization form of the Hamiltonian. In Hückel calculations you describe a molecule as having an energy coulomb integral alpha. This is the energy of a site. To do a | This is the second quantization form of the Hamiltonian. In Hückel calculations you describe a molecule as having an energy coulomb integral α. This is the energy of a site. To do a Hückel calculation for a polyene molecule you place an α on each carbon. The value of the α is the value of the π atomic orbital for an isolated sp2 carbon. | ||
The transfer integral ( | The transfer integral (t<sub>mn</sub>) or electron coupling for adjacent molecules is the resonance integral beta in Hückel terminology. For example considering butadiene at the Hückel level there would be 4 carbons, each with a site energy α, and between carbons the resonance integral β, which can be different for double B<sub>1</sub> (shorter bonds have larger electronic coupling) and single bonds B<sub>2</sub>. The same could be done for the pentacene system. In the case of pentacene the two molecules of the units cells have slightly different surroundings and therefore the energies would slightly different. There would be β1 and β2 (for the tb and td directions). In the Hamiltonian α and β become e and t. This gives a very compact way of writing an equation. | ||
<br clear='all'> | |||
=== Electron phonon mechanism === | === Electron phonon mechanism === | ||
[[Image:electron_phonon.png|thumb|400px|Local e-ph coupling (Holstein's molecular polaron model) and nonlocal e-ph coupling (Peierls-type model Su Schrieffer-Heeger Hamiltonian)]] | |||
Intramolecular and intramolecular modes of vibration are able to modify e and t. To get a complete description of the system you can look at the variation of the site energy as a function each the vibrational modes that are in the system. This equation looks at the site energy on molecule m and zero denotes the absence of vibration and then look at the impact of each of the vibrational modes (j) on the site. This shows the variation of site energy as you take into account vibrational modes. Some modes will have no impact, some will be significant. Moving to an ionized state there will be a strong geometry relaxation so there will be a strong coupling to the vibrational modes that lead to the ionized state. | |||
Intramolecular and intramolecular modes of vibration are able to modify e | |||
The effect of temperature can be explained because the increased temperature causes excited levels of vibration with larger displacement, and large perturbation of the site energies. The same can be done for the transfer integrals. When you displace molecules from a perfectly cofacial orientation there were major variations in the electronic coupling. So this will have a large impact the transfer integral. | The effect of temperature can be explained because the increased temperature causes excited levels of vibration with larger displacement, and large perturbation of the site energies. The same can be done for the transfer integrals. When you displace molecules from a perfectly cofacial orientation there were major variations in the electronic coupling. So this will have a large impact the transfer integral. | ||
Considering the impact of vibrations on the site energy that is referred to as the “local” electron-phonon coupling. If you look at the impact on the transfer integral that is called the “nonlocal” electron-phonon coupling. In the last 40 years there have theories that take into account one or the other of these couplings, such as Holstein’s molecular polar model (local only), and the Peierls type model (nonlocal only), or Su-Schrieffer-Heeger Hamiltonian. These are all simple Hueckle theory varying beta depends on the bond length, and electronic coupling depends on bond C-C bond stretching. | Considering the impact of vibrations on the site energy that is referred to as the “local” electron-phonon coupling. If you look at the impact on the transfer integral that is called the “nonlocal” electron-phonon coupling. In the last 40 years there have theories that take into account one or the other of these couplings, such as Holstein’s molecular polar model (local only), and the Peierls type model (nonlocal only), or Su-Schrieffer-Heeger Hamiltonian. These are all simple Hueckle theory varying β depends on the bond length, and electronic coupling depends on bond C-C bond stretching. β or t vary depending on the mode. | ||
=== Local electron-phonon coupling === | === Local electron-phonon coupling === | ||
[[Image:Local_coupling.png|thumb|300px|Local electron-phonon coupling]] | |||
Local electron-phonon coupling is the impact of vibrations from molecular relaxations (intra-molecular modes) on site energy. There will be an impact from the polarization (intramolecular modes) as well librations (translations and rotations of molecule as whole) in intermolecular modes. | |||
Local electron-phonon coupling is the impact of vibrations from molecular relaxations (intra-molecular modes) on site energy | |||
The local electron-phonon coupling can be very significant due to intramolecular geometry relaxations | The local electron-phonon coupling can be very significant due to intramolecular geometry relaxations | ||
The polarization contributions still need more systematic investigations | The polarization contributions still need more systematic investigations | ||
<br clear='all'> | |||
=== | === Nonlocal electron-phonon coupling === | ||
[[Image:Nonlocal_coupling.png|thumb|300px|Nonlocal electron-phonon coupling]] | |||
Non local electron-phonon coupling is mostly a functon of intermolecular modes. Nonlocal electron-phonon coupling is large. This does not depend very much on the intermolecular geometry. Use the Condon approximation which says whatever geometry you used for the intramolecular electron coupling will be pretty much the same for the intermolecular geometry. | |||
<br clear='all'> | |||
[[Image:napthalene_opticalmodes.png|thumb|500px|Intermolecular optical modes in naphthalene<ref>Spectrochim. Acta, Part A A24, 1091 (1968)</ref> | |||
]] | |||
This shows the intermolecular optical modes in naphthalene. These can be evaluated and they have good agreement with experimental observation. | This shows the intermolecular optical modes in naphthalene. These can be evaluated and they have good agreement with experimental observation. | ||
Currently we can not predict the crystal structure given the chemical formula of a molecule. Given a molecule the big challenge is to evaluate the mobility as a function temperature. | Currently we can not predict the crystal structure given the chemical formula of a molecule. Given a molecule the big challenge is to evaluate the mobility as a function temperature. | ||
<br clear='all'> | |||
=== Charge Transport === | |||
[[Image:chargetransport.png|thumb|400px|Variation in charge mobility with temperature]] | |||
Currently we can not predict the crystal structure of a molecule given the chemical formula of a molecule. The big challenge is to evaluate the mobility as a function of temperature. Starting with a perfect crystal at low temperature there is a large mobility. As the temperature increases the molecules start vibrating and there is a reduction in electronic coupling, bandwidth and mobility. In metals as you increase temperature the vibrations get larger and mobility comes down. At some point the vibrations will reduce the electronic coupling so much that it will become favorable for the charge carrier to localize. This cross over region is difficult to describe and may not be an abrupt evolution. There is a gradual localization process. | |||
Crossing over into the hopping regime (an activated regime) with localization the mobility goes back up with temperature. Here the vibrations help by preparing the two molecules to achieve essentially the same geometry so that electron transfer can take place. So the rate of electron transfer is simply the time it takes for vibrations to bring the molecules into the same geometry. In most organic materials will have decomposed before they reach a temperature where they begin to decrease in electron transfer with temperature (T<sub>2</sub>). | |||
[[category:transport properties]] | |||
== References == | |||
<references/> | |||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
<td style="text-align: left; width: 33%">[[ | <td style="text-align: left; width: 33%">[[Marcus Theory and Reorganization Energy|Previous Topic]]</td> | ||
<td style="text-align: center; width: 33%">[[Main_Page#Transport Properties|Return to Transport Properties Menu]]</td> | <td style="text-align: center; width: 33%">[[Main_Page#Transport Properties|Return to Transport Properties Menu]]</td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Latest revision as of 11:40, 7 July 2010
| Previous Topic | Return to Transport Properties Menu |
The frontier of research in organic semiconductors is attempting to get a complete picture of electron transport by understanding intramolecular and intermolecular vibrations or phonons and electron-phonon coupling. Several people have been working on this for a while. Silbey & Munn Bobbert et al. Troisi et al. Stafström et al. Shuai et al.
Tight-binding Hamiltonian
This is the second quantization form of the Hamiltonian. In Hückel calculations you describe a molecule as having an energy coulomb integral α. This is the energy of a site. To do a Hückel calculation for a polyene molecule you place an α on each carbon. The value of the α is the value of the π atomic orbital for an isolated sp2 carbon.
The transfer integral (tmn) or electron coupling for adjacent molecules is the resonance integral beta in Hückel terminology. For example considering butadiene at the Hückel level there would be 4 carbons, each with a site energy α, and between carbons the resonance integral β, which can be different for double B1 (shorter bonds have larger electronic coupling) and single bonds B2. The same could be done for the pentacene system. In the case of pentacene the two molecules of the units cells have slightly different surroundings and therefore the energies would slightly different. There would be β1 and β2 (for the tb and td directions). In the Hamiltonian α and β become e and t. This gives a very compact way of writing an equation.
Electron phonon mechanism
Intramolecular and intramolecular modes of vibration are able to modify e and t. To get a complete description of the system you can look at the variation of the site energy as a function each the vibrational modes that are in the system. This equation looks at the site energy on molecule m and zero denotes the absence of vibration and then look at the impact of each of the vibrational modes (j) on the site. This shows the variation of site energy as you take into account vibrational modes. Some modes will have no impact, some will be significant. Moving to an ionized state there will be a strong geometry relaxation so there will be a strong coupling to the vibrational modes that lead to the ionized state.
The effect of temperature can be explained because the increased temperature causes excited levels of vibration with larger displacement, and large perturbation of the site energies. The same can be done for the transfer integrals. When you displace molecules from a perfectly cofacial orientation there were major variations in the electronic coupling. So this will have a large impact the transfer integral.
Considering the impact of vibrations on the site energy that is referred to as the “local” electron-phonon coupling. If you look at the impact on the transfer integral that is called the “nonlocal” electron-phonon coupling. In the last 40 years there have theories that take into account one or the other of these couplings, such as Holstein’s molecular polar model (local only), and the Peierls type model (nonlocal only), or Su-Schrieffer-Heeger Hamiltonian. These are all simple Hueckle theory varying β depends on the bond length, and electronic coupling depends on bond C-C bond stretching. β or t vary depending on the mode.
Local electron-phonon coupling
Local electron-phonon coupling is the impact of vibrations from molecular relaxations (intra-molecular modes) on site energy. There will be an impact from the polarization (intramolecular modes) as well librations (translations and rotations of molecule as whole) in intermolecular modes.
The local electron-phonon coupling can be very significant due to intramolecular geometry relaxations
The polarization contributions still need more systematic investigations
Nonlocal electron-phonon coupling
Non local electron-phonon coupling is mostly a functon of intermolecular modes. Nonlocal electron-phonon coupling is large. This does not depend very much on the intermolecular geometry. Use the Condon approximation which says whatever geometry you used for the intramolecular electron coupling will be pretty much the same for the intermolecular geometry.
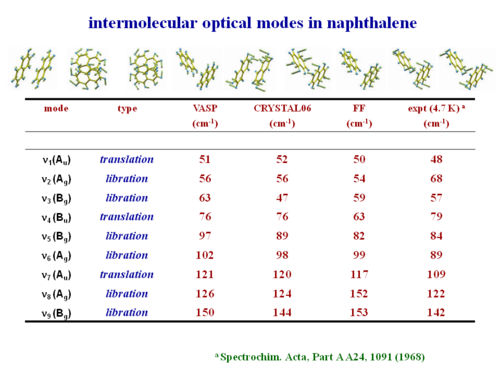
This shows the intermolecular optical modes in naphthalene. These can be evaluated and they have good agreement with experimental observation.
Currently we can not predict the crystal structure given the chemical formula of a molecule. Given a molecule the big challenge is to evaluate the mobility as a function temperature.
Charge Transport
Currently we can not predict the crystal structure of a molecule given the chemical formula of a molecule. The big challenge is to evaluate the mobility as a function of temperature. Starting with a perfect crystal at low temperature there is a large mobility. As the temperature increases the molecules start vibrating and there is a reduction in electronic coupling, bandwidth and mobility. In metals as you increase temperature the vibrations get larger and mobility comes down. At some point the vibrations will reduce the electronic coupling so much that it will become favorable for the charge carrier to localize. This cross over region is difficult to describe and may not be an abrupt evolution. There is a gradual localization process.
Crossing over into the hopping regime (an activated regime) with localization the mobility goes back up with temperature. Here the vibrations help by preparing the two molecules to achieve essentially the same geometry so that electron transfer can take place. So the rate of electron transfer is simply the time it takes for vibrations to bring the molecules into the same geometry. In most organic materials will have decomposed before they reach a temperature where they begin to decrease in electron transfer with temperature (T2).
References
- ↑ Spectrochim. Acta, Part A A24, 1091 (1968)
| Previous Topic | Return to Transport Properties Menu |




