Difference between revisions of "Sigma and pi Orbitals"

From CleanEnergyWIKI
Jump to navigation Jump to search
 
(65 intermediate revisions by 3 users not shown)
Line 1: Line 1:
[[Main_Page#Molecular Orbitals|Return to Molecular Orbitals Menu]] | 
<table id="toc" style="width: 100%">
[[Polarization and Polarizability|Next Topic]]
<tr>
Polarization is an important concept in designing electro optical materials.
<td style="text-align: left; width: 33%">[[Electronegativity and Bonding Between Atoms|Previous Topic]]</td>
<td style="text-align: center; width: 33%">[[Main_Page#Molecular Orbitals|Return to Molecular Orbitals Menu]]</td>
<td style="text-align: right; width: 33%">[[Polarization and Polarizability|Next Topic]]</td>


</tr>
</table>


=== Mechanisms for polarization ===


If you have any mechanism to apply an external electrical field this may lead to polarization of the molecules.
In electronic polarization the field pulls electrons more than it repells the nucleus because electrons are far lighter than the protons and neutrons. The timescale for polarization of a atom due to a field is 10 -15 seconds. This is about as fast as you can do things.


If two atoms with unequal electronegavity are bonded the molecule will have a dipole moment. A vibration of the atoms results in a change in the position of the nuclei and the electrons follow the nuclei. This happens on a timescale of picoseconds. Infrared leads to vibrations of molecules. The reciprocal of the frequency of IR has a time constant of 100 femptoseconds.
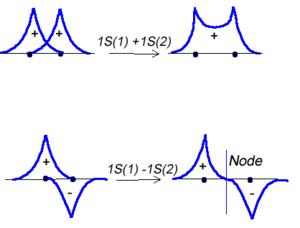
[[Image:2sigma_orbitals.png|thumb|300px|Hydrogen 1 and Hydrogen 2 combine to form a new molecular orbital.]]


You can have molecules that already have a dipole moment and place them in an electronic field the molecules will align. This time constant for this rotation is in the area of 10s of nanoseconds. Microwave radiation can be used to cause rotations in molecules.
=== Molecular Orbital Theory ===


If there are ions in the presence of an electric field there will be a bulk motion. If there is an oscillating electronic field it needs to be matched to the timescale of the polarization mechanism. Only those components that react as fast or faster than the frequency will make a contribution to the bulk polarization of the material. The following animation demonstrates these four types.
Molecular orbital theory was developed in the early part of the last century to help rationalize why bonds form and to explain the properties of molecules. In molecular orbital theory the atomic orbitals from each atom can overlap with those on other atoms. Since the atomic orbitals are wavefunctions and behave like waves it is possible for them to overlap in a constructive manner to form a bonding orbital.


<swf width="500" height="400">http://depts.washington.edu/cmditr/media/01 Polarization Mechanisms.swf</swf>
:<math>\Psi_{new} = \Psi_1 + \Psi_2\,\!</math>


Here is an hydrogen atom in an oscillating electric field. The atom is is oscillating as the electrons are being displaced and the energy levels are changing.
Or the two functions can combine in a destructive manner.


[[Image:Hydrogen_polar.gif]]
:<math>\Psi_{new} = \Psi_1 - \Psi_2\,\!</math>


In an atom with &pi; orbitals there is more polarizability in the &pi; orbitals than in the &sigma; orbitals. Dyes are typically &pi; conjugated compounds because &pi; orbitals are more polarizable in the visible spectrum.
This is sometimes referred to as Linear Combination of Atomic Orbitals (LCAO). When there is a destructive combination of the two waves there is a node between the two atoms where there is a zero probability of finding the electron. The first case is known as a bonding orbital and the latter case is known as an anti-bonding orbital.  


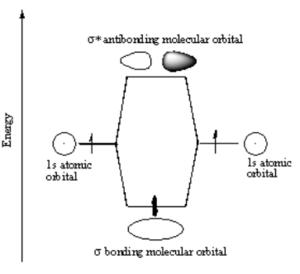
[[Image:PI orbit anim.gif]]
[[Image:H2_antibonding_orbital.png|thumb|300px|Electrons from two atoms combine to form a &sigma; bonding molecular orbital.]]
Note that the electron density is higher between the nuclei in the bonding molecular orbital and the that the orbital is stabilized, that is lower in energy relative to the two isolated hydrogren atoms. The sign of both wavefunctions is positive. There is a decreased electron density between the atoms in the antibonding molecular orbital and the orbital is destabilized, that is higher in energy than the two isolated hydrogen atoms. In very simple molecular orbital theory we treat the destabilization energy of the antibonding orbital as identical to the stabilization energy of the bonding orbital but in fact it is slightly more destabilized than the bond orbital is stabilized.
<br clear='all'>


See [http://www.chem1.com/acad/webtext/chembond/cb08.html An Introduction to molecular orbital theory]


=== Linear polarizability ===
=== Orbital Overlap ===
[[Image:Dipole_align.jpg|thumb|300px|]]
[[Image:Sigma_bond.png|thumb|300px|The sign of wavefunctions is shown as light and dark lobes.]]


Molecules that have a dipole moment will orient in an electric field. These are known as second order non-linear material. The force that is on the system is a torque that is related to angle between dipole and the electric field, and upon the magnitude of the field and the dipole. If the molecule is aligned with the field it will not feel a torque. If it oriented at 90 degrees it will feel a substanstial torque.
The amount of stabilization or destabilization is referred to a their orbital overlap. Mathematically the overlap is an integral of from negative infinity to positive infinity of a product of two wavefunctions over all space.


Dipole is vector quantity, it has a magnitude and a direction. An opposite field will induce a dipole in the opposite direction.
:<math>\int_{-\infty}^{\infty} \Psi_1^* \Psi_2 dxdydz\,\!</math> = Overlap
 
If you plot dipole moment against the electric field you get a straight line. The slope (&alpha;) of the line for the function is the linear polarizability. A higher &alpha; means a greater amount of polarization for the same amount of applied field.
 
[[Image:polar_plot.JPG|thumb|300px|]]
 
<math>\mu = \alpha \Epsilon\,\!</math>


The area under the curve for these functions is the orbital overlap.
<br clear='all'>
<br clear='all'>
=== Anisotropic Polarizability ===
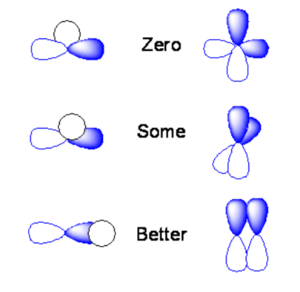
[[Image:Orbital_overlap.png|thumb|300px|Possible overlap of orbitals]]
If the s orbital is lined up exactly over the node of a p orbital you will end up with positive overlap on one side, and equal and opposite overlap on the other side. The orbital overlap when you integrate over all space will be identically zero. If you take two p orbitals that are oriented at 90 degrees the product is zero.


[[Image:anisotropic_polar.JPG|thumb|300px|]]
If you shift the s orbital a little bit one direction the overlap of the s orbital with one of the lobes will be non-zero.  If you have two p orbitals at some angle you will have non-zero overlap. Or if a s orbital overlaps only on side of a the p orbital you would get some orbital overlap.  


An organic molecule, 2-4 Hexadi-ine has two triple bonds and single bonds between two of the carbons. The triple bonds form a cylinder of electrons. If you apply and electic field along the long axis of the cyclinder you will get a larger induced dipole moment. If you assume that the polarizability at 90degrees to the axis is negible compare to the that of the along the long axis then electrons are going to move along the axis only. The interaction of the electric field with the electrons is greatest in long direction, and becomes zero at 90 degrees. This can be described as a dot product, a cosine function. An oscillating field will cause electrons to move up and down along the long axis and creates an induced dipole. Molecules that are oriented at 45 degree angle will have some induced dipole due to the applied field. This induced field can be used with cross polarizers to allow or not allow light to pass through the material.
The two p orbitals that are aligned with the same sign will have the maxiumum orbital overlap and the maxium bonding interaction. If they are overlapping with opposite signs you have the maximum anti-bonding interaction. If you rotate them orthogonally they will be neither bonding or nor antibonding.




=== Tensor calculation ===
<br clear='all'>


To describe the polarizability of this kind of molecule you have to use a tensor to describe all the components of polarizability. It is possible to apply an electric field along y but induce a dipole moment along y. Each entry of the tensor is a component of the polarizability.
=== p-p &sigma; Bonding ===


<math>\begin{pmatrix}
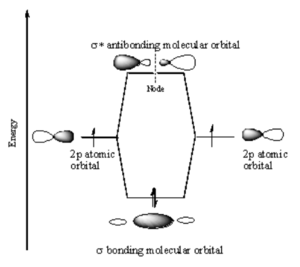
[[Image:P_orbital_overlap.png|thumb|300px|P atomic orbitals combine to form $sigma; molecular orbitals]]
\mu_x\\
Two p orbitals can combine contructively or destructively. In constructive situation you have a lower energy bonding orbital. If they align destructively you have the higher energy antibonding orbital.
\mu_y\\
In a &sigma; bond, if you look down the axis between the atoms bonded to each other, the orbital will appear cylindrically symmetric. In such cases the atoms at the end of the bonds can rotate without breaking the bond. This is the case from the bonds between the s orbitals in hydrogen. P orbitals can overlap in two different ways. If they overlap head-on a &sigma; bond is formed.<br clear='all'>
\mu_z
\end{pmatrix}
= \begin{pmatrix}
\alpha_{xx}& \alpha_{xy}& \alpha_{xz} & \\
\alpha_{yx}& \alpha_{yy}& \alpha_{yz} & \\
\alpha_{zx}& \alpha_{zy}& \alpha_{zz} &
\end{pmatrix}
=
\begin{pmatrix}
E_x  \\
E_y  \\
E_z 
\end{pmatrix}
\,\!</math>


You can calculate the degree of polarization in any direction with the tensor product;
<br clear='all'>


<math>\mu_x = \alpha_{xx} E_x + \alpha_{xy} E_y + \alpha_{xz} E_z\,\!</math>
=== p-p &pi; Bonding ===
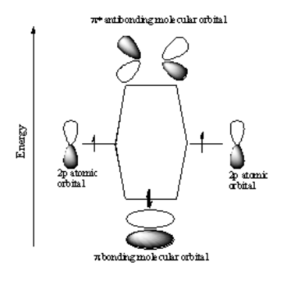
[[Image:Pi bond.png|thumb|300px|P atomic orbitals form &pi; molecular orbitals.]]
If two p-orbitals overlap constructively then a &pi; bond is formed. If you look down the axis of a &pi; bond the orbital will not appear cylindrically symmetrical. The top has one sign the bottom has the opposite sign. There will be a node in the plane of the bond. The overlap of the orbital depends on critically on the angle between the orbitals. If the orbitals are not exactly lined up, the bond will begin to break and at 90&deg; there be no &pi;bonding.  The stabilization of two p orbitals forming a &sigma; bond is greater than two p orbitals forming a &pi; bonds because p  and &sigma; bonds have more orbital overlap. As a consequence &sigma; bonds are more stabilized and stonger than &pi; bonds.


[[Image:Balloon_deformation.png|thumb|300px|]]
<br clear='all'>
Consider the electric field is a deforming force and the dipole moment is the deformation. The balloon can be stretched in one direction resulting in changes in the other dimensions. A balloon could be isotropic meaning it would be equally easy to stretch in all directions. Or it could have fibers built in that would limit the deformation along one axis. An electric field from any direction can induce a dipole in any direction. The components along the diagonal tend to be the strongest.  It is possible to have more than one electric field applied (along x and y). To describe this situation you actually need a 3 x 3 x 3 (third rank) tenso, a  matrix with 27 components.
=== Effect of field on &pi; electrons ===
You could even have 3 electric fields with 81 components.


[[Image:PI_orbit_anim.gif‎]]


=== Dielectric Constant ===
We use the dielectric constant we often are referring to a solvent. A refractive index refers to speed of light. For a bulk material we describe the polarization density in a material. Instead of looking at a single molecule, we can look at the polarizability of the entire bulk material induced by an elecric field.


In bulk materials, the linear polarization is given by:
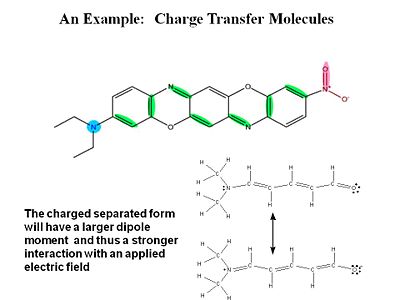
[[Image:chargetransfer.JPG|thumb|400px|The charge-separated form of this mole will react more to an applied field.]]
&sigma; electrons have electron density between the nuclei so they are tightly bound and do not change position as much when exposed to an external field. &pi; electrons have the electron density above and below of the plane of the nuclei. When you apply a field you change the distribution and induce a dipole.


<math>P_i(\omega) =  \sum_{ij}\chi_{ij}(\mu)E_j(\omega)\,\!</math> (4)


where
<math>\chi_i( \omega )\,\!</math> is the polarization density in direction i.


<math>\omega\,\!</math> is the frequency
For a typical molecule you go from a neutral ground state to a charge separated state by application of an electric field. Quantum -mechanically the electric field causes a mixing of these two states.


<math>\chi_{ij}(\omega)\,\!</math> is the linear susceptibility of an ensemble of molecules.
=== Covalent bonding ===
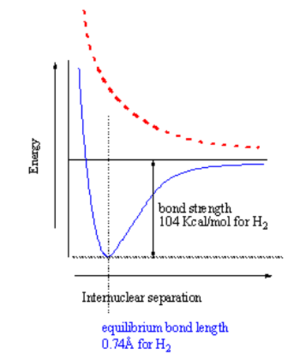
[[Image:H2bondstrength.png|thumb|300px|Energy vs distance for bonding (blue) and excited state (red)]]


Note that the vectorial and tensor aspects of E and <math>\chi\,\!</math> have been ignored to simplify notation.
When two atoms with duets or octets that have not been satisfied get within close proximity, they can interact in such a way as to create a bond by "sharing" electrons. Sharing of electrons can achieve a stable electron configuration corresponding to a noble gas configuration. On the right side of the diagram the hydrogen atoms are far apart and do not interact. As they move closer the system is stabilized by the formation of a bond through overlap of their orbitals and the lowering of the kinetic energy of the system. If the atoms get too close there will be an extremely strong nuclear - nuclear repulsion that greatly destabilizes the system. The correct balance between these interactions is found at the equilibrium bond length.


The total electric field (the "displaced" field, D) within the material  becomes:
How does the potential energy surface for a hydrogen-hydrogen &sigma; bond in the ground state (where the electrons are in the lower orbital) vs the excited states (ie where one electron is in an antibonding orbital)? These two states have a different energy dependence as a function of distance. A &sigma; bonding combination initially becomes increasingly stabilized as you move from infinity until the point where the internuclear interaction (repulsion between protons) causes the energy to increase greatly. This point for hydrogen occurs at a distance of about .74 Å. The bond strength is 104 Kcal/mol, which is a very strong bond. The equilibrium constant for hydrogen radicals vs bond hydrogen would be 99999999.... favoring the bound state.


In the excited state the electrons are increasingly destabilized as the atoms get closer, the surface is repulsive. If you have two atoms infinitely far apart the system is neither stabilized nor destabilized. If you bring atoms to a correct geometry the ground state is stabilized. If you bring them too close you get a destabilized state. The excited state is always increasingly destabilized with decreasing distance.
[[category:molecular orbitals]]
<br clear='all'>
<table id="toc" style="width: 100%">
<tr>
<td style="text-align: left; width: 33%">[[Electronegativity and Bonding Between Atoms|Previous Topic]]</td>
<td style="text-align: center; width: 33%">[[Main_Page#Molecular Orbitals|Return to Molecular Orbitals Menu]]</td>
<td style="text-align: right; width: 33%">[[Polarization and Polarizability|Next Topic]]</td>


<math>D  =  E  +  4\pi P  =  (1  +  4\pi \chi)E \,\!</math>  (5)
</tr>
 
</table>
 
<math>P  =  \chi E\,\!</math> (Equation (4)),  <math>4 \pi \chi E\,\!</math> is the internal electric field created by the induced displacement (polarization) of charges.
 
 
=== The Dielectric Constant ===
The dielectric constant and the refractive index n(&omega;) are two bulk parameters that characterize the susceptibility of a material. 
&epsilon; (&omega) in a given direction is defined as the ratio of the displaced internal field to the applied field (&epsilon; = D/E) in that direction.
 
<math>\epsilon_{ij} (\omega) = 1 + 4\mu \chi_{ij} (\omega)\,\!</math>  (6)
The dielectric constant of the material relates to the susceptiblity of the material, which relates to the polarizability of the molecules. Since $chi; is frequency dependent because of the different mechanisms that can induce polarization,  then &epsilon; the dielectric constant is also frequency dependent.
 
The frequency dependence of the dielectric constant provides insight into the mechanism of charge polarization. with low frequency you can get contribution from electronic, vibronic, and rotational polarization. As you increase the frequency the dielectric constant drops until the point where the only contributing factor is the electronic polarization.
[[Image:Freq_dielectric.jpg|thumb|300px|]]
 
The ratio of the speed of light in a vacuum, c, to the speed of light in a material, v, is called the index of refraction (n):
 
<math>n  =  \frac {c}{v}\,\!</math> (7)
Index of refraction is typically measured at low frequencies. At optical frequencies the dielectric constant equals the square of the refractive index:
<math>\epsilon_\infty(\omega) =  n^2(\omega)\,\!</math> (8)
 
Consequently, we can relate the refractive index to the bulk linear (first-order) susceptibility:
<math>n^2(\omega ) = 1+ 4\pi \chi(\omega)\,\!</math> (9)
Index of refraction depends therefore on chemical structure. For example iodine has a higher index of refraction than fluorine because iodine is has a higher electron affinity, and therefore has more polarizability, so as material it has as a material greater susceptibility, therefore the refractive index is higher. This is a simple and essential factor of optics. As an organic chemist you can manipulate the atoms of a molecule to change the polarizability and thereby control the optical properties of the material.
 
=== Birefringence ===

Latest revision as of 16:14, 21 December 2009

Previous Topic Return to Molecular Orbitals Menu Next Topic


Hydrogen 1 and Hydrogen 2 combine to form a new molecular orbital.

Molecular Orbital Theory

Molecular orbital theory was developed in the early part of the last century to help rationalize why bonds form and to explain the properties of molecules. In molecular orbital theory the atomic orbitals from each atom can overlap with those on other atoms. Since the atomic orbitals are wavefunctions and behave like waves it is possible for them to overlap in a constructive manner to form a bonding orbital.

<math>\Psi_{new} = \Psi_1 + \Psi_2\,\!</math>

Or the two functions can combine in a destructive manner.

<math>\Psi_{new} = \Psi_1 - \Psi_2\,\!</math>

This is sometimes referred to as Linear Combination of Atomic Orbitals (LCAO). When there is a destructive combination of the two waves there is a node between the two atoms where there is a zero probability of finding the electron. The first case is known as a bonding orbital and the latter case is known as an anti-bonding orbital.

Error creating thumbnail: Unable to save thumbnail to destination
Electrons from two atoms combine to form a σ bonding molecular orbital.

Note that the electron density is higher between the nuclei in the bonding molecular orbital and the that the orbital is stabilized, that is lower in energy relative to the two isolated hydrogren atoms. The sign of both wavefunctions is positive. There is a decreased electron density between the atoms in the antibonding molecular orbital and the orbital is destabilized, that is higher in energy than the two isolated hydrogen atoms. In very simple molecular orbital theory we treat the destabilization energy of the antibonding orbital as identical to the stabilization energy of the bonding orbital but in fact it is slightly more destabilized than the bond orbital is stabilized.

See An Introduction to molecular orbital theory

Orbital Overlap

The sign of wavefunctions is shown as light and dark lobes.

The amount of stabilization or destabilization is referred to a their orbital overlap. Mathematically the overlap is an integral of from negative infinity to positive infinity of a product of two wavefunctions over all space.

<math>\int_{-\infty}^{\infty} \Psi_1^* \Psi_2 dxdydz\,\!</math> = Overlap

The area under the curve for these functions is the orbital overlap.

Possible overlap of orbitals

If the s orbital is lined up exactly over the node of a p orbital you will end up with positive overlap on one side, and equal and opposite overlap on the other side. The orbital overlap when you integrate over all space will be identically zero. If you take two p orbitals that are oriented at 90 degrees the product is zero.

If you shift the s orbital a little bit one direction the overlap of the s orbital with one of the lobes will be non-zero. If you have two p orbitals at some angle you will have non-zero overlap. Or if a s orbital overlaps only on side of a the p orbital you would get some orbital overlap.

The two p orbitals that are aligned with the same sign will have the maxiumum orbital overlap and the maxium bonding interaction. If they are overlapping with opposite signs you have the maximum anti-bonding interaction. If you rotate them orthogonally they will be neither bonding or nor antibonding.



p-p σ Bonding

P atomic orbitals combine to form $sigma; molecular orbitals

Two p orbitals can combine contructively or destructively. In constructive situation you have a lower energy bonding orbital. If they align destructively you have the higher energy antibonding orbital. In a σ bond, if you look down the axis between the atoms bonded to each other, the orbital will appear cylindrically symmetric. In such cases the atoms at the end of the bonds can rotate without breaking the bond. This is the case from the bonds between the s orbitals in hydrogen. P orbitals can overlap in two different ways. If they overlap head-on a σ bond is formed.


p-p π Bonding

P atomic orbitals form π molecular orbitals.

If two p-orbitals overlap constructively then a π bond is formed. If you look down the axis of a π bond the orbital will not appear cylindrically symmetrical. The top has one sign the bottom has the opposite sign. There will be a node in the plane of the bond. The overlap of the orbital depends on critically on the angle between the orbitals. If the orbitals are not exactly lined up, the bond will begin to break and at 90° there be no πbonding. The stabilization of two p orbitals forming a σ bond is greater than two p orbitals forming a π bonds because p and σ bonds have more orbital overlap. As a consequence σ bonds are more stabilized and stonger than π bonds.


Effect of field on π electrons

Error creating thumbnail: Unable to save thumbnail to destination


The charge-separated form of this mole will react more to an applied field.

σ electrons have electron density between the nuclei so they are tightly bound and do not change position as much when exposed to an external field. π electrons have the electron density above and below of the plane of the nuclei. When you apply a field you change the distribution and induce a dipole.


For a typical molecule you go from a neutral ground state to a charge separated state by application of an electric field. Quantum -mechanically the electric field causes a mixing of these two states.

Covalent bonding

Energy vs distance for bonding (blue) and excited state (red)

When two atoms with duets or octets that have not been satisfied get within close proximity, they can interact in such a way as to create a bond by "sharing" electrons. Sharing of electrons can achieve a stable electron configuration corresponding to a noble gas configuration. On the right side of the diagram the hydrogen atoms are far apart and do not interact. As they move closer the system is stabilized by the formation of a bond through overlap of their orbitals and the lowering of the kinetic energy of the system. If the atoms get too close there will be an extremely strong nuclear - nuclear repulsion that greatly destabilizes the system. The correct balance between these interactions is found at the equilibrium bond length.

How does the potential energy surface for a hydrogen-hydrogen σ bond in the ground state (where the electrons are in the lower orbital) vs the excited states (ie where one electron is in an antibonding orbital)? These two states have a different energy dependence as a function of distance. A σ bonding combination initially becomes increasingly stabilized as you move from infinity until the point where the internuclear interaction (repulsion between protons) causes the energy to increase greatly. This point for hydrogen occurs at a distance of about .74 Å. The bond strength is 104 Kcal/mol, which is a very strong bond. The equilibrium constant for hydrogen radicals vs bond hydrogen would be 99999999.... favoring the bound state.

In the excited state the electrons are increasingly destabilized as the atoms get closer, the surface is repulsive. If you have two atoms infinitely far apart the system is neither stabilized nor destabilized. If you bring atoms to a correct geometry the ground state is stabilized. If you bring them too close you get a destabilized state. The excited state is always increasingly destabilized with decreasing distance.

Previous Topic Return to Molecular Orbitals Menu Next Topic
Retrieved from "http://cleanenergywiki.org/index.php?title=Sigma_and_pi_Orbitals&oldid=5838"