Difference between revisions of "Total Internal Reflection"

From CleanEnergyWIKI
Jump to navigation Jump to search
m
 
(61 intermediate revisions by 2 users not shown)
Line 1: Line 1:
[[Image:reflexion totale interne.png|thumb|right|250px|The larger the angle to the normal, the smaller is the fraction of light transmitted, until the angle when '''total internal reflection''' occurs.  (The color of the rays is to help distinguish the rays, and is not meant to indicate any color dependence.)]]
<table id="toc" style="width: 100%">
'''Total internal reflection''' is an [[optical phenomenon]] that occurs when a ray of light strikes a medium boundary at an angle larger than the '''critical angle''' with respect to the normal to the surface. If the [[refractive index]] is lower on the other side of the boundary no light can pass through, so effectively all of the light is [[Reflection (physics)|reflected]]. The critical angle is the [[angle of incidence]] above which the total internal reflection occurs.
<tr>
<td style="text-align: left; width: 33%">[[Optical Fibers|Previous Topic]]</td>
<td style="text-align: center; width: 33%">[[Main_Page#Optical Fibers, Waveguides, and Lasers|Return to Optical Fibers, Waveguides, and Lasers Menu]]</td>
<td style="text-align: right; width: 33%">[[Planar Dielectric Waveguides|Next Topic]]</td>
</tr>
</table>


<div style="{{Robelbox/pad}}; font-size:90%; height:300px; overflow:auto;">
== Total Internal Reflection ==
You can browse Wikiversity by the completion status of resources, which can help you find complete resources reading for using, or freshly started ones which you can help develop. Work also needs to be done on categorising resources by completion status, which is why some of the categories here are rather empty.
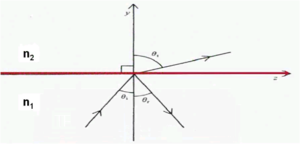
[[Image:Snellslaw.png|thumb|300px| When &theta;<sub>1</sub> > &theta;<sub>1c</sub> light can not enter medium n<sub>2</sub>]]
{{#categorytree:Resources by completion status|mode=all|depth=10|hideroot}}
 
</div>
A critical concept in the case of optical fibers is the concept of total internal reflection. The bending of light as it goes from one medium into another is related to the index of reflection of the materials (n<sub>1</sub> and n<sub>2</sub>). By Snell's law when n<sub>1</sub> > n<sub>2</sub> then &theta; <sub>1</sub> is less than &theta;<sub>2</sub>. As you decrease the angle &theta;<sub>1</sub> and bring the light closer to parallel with the interface you reach a critical angle &theta;<sub>1c</sub> where there is total internal reflection.
 
Snells laws are also known as Fresnel's Equations:
 
:<math>\theta _i = \theta _r\,\!</math> 
 
and
 
:<math>\frac {sin \theta_i} {\theta_t} = \frac {n_2} {n_1}\,\!</math>
 
where
:<math>\theta_i\,\!</math> is the angle of incidence
 
:<math>\theta_r\,\!</math> is the angle of reflection
 
:<math>\theta_{c} = sin^{-1}(\frac {n_2} {n_1} )\,\!</math>
 
where:
:<math>\theta_{c}\,\!</math> is the critical angle
 
:<math>n_1 , n_2\,\!</math> are the index of refraction of the two media
 
 
if &theta;<sub>1</sub> keeps Increasing: &theta;<sub>2</sub> approaches 90°
 
for a critical angle Θ<sub>1</sub>, Θ<sub>2</sub> = 90°and the beam emerges along the surface
 
When
 
:<math>\theta_2 = 90° \rightarrow sin \theta_2 = 1\,\!</math>
 
:<math>\theta_{1c}  = sin^{-1} \left (\frac {n_2} {n_1} \right )\,\!</math>
 
 
and when
 
:<math>\theta_1 > \theta_{1c}\,\!</math> there is total reflection
 
In this case there is no transmitted light in the second medium (the irradiance of the reflected and incident beams is equal). Light interacts at the interface and there is a phase shift between the incident and the reflected beams which is dependent on the two materials.
 
This is a critical process in optical fibers and waveguides because it can carry light for long distances. For these values of index of refraction you get a critical angle of 78.6 which means the light must be very nearly parallel to the interface.
 
for n<sub>1</sub> = 1.53 and n<sub>2</sub> = 1.50 : &theta;<sub>1c</sub> = 78.6°
 
 
 
<br clear='all'>
 
=== Simulations ===
 
 
This flash simulation shows how total internal reflection and minimum radius of turns depends on the diameter of the optical fiber. The diameter changes how much of the light is below the critical angle where it is fully reflected.
 
<swf width="500" height="400">http://concave.stc.arizona.edu/thepoint/Interactive/ofiber.swf</swf>
 
 
This simulation allows you to select combinations of materials with different indexes of refraction. Try to get the best combination to achieve total internal reflection.
<swf width="500" height="400">http://concave.stc.arizona.edu/thepoint/Interactive/ofiberapp2.swf</swf>
 
[[category:light]]
<table id="toc" style="width: 100%">
<tr>
<td style="text-align: left; width: 33%">[[Optical Fibers|Previous Topic]]</td>
<td style="text-align: center; width: 33%">[[Main_Page#Optical Fibers, Waveguides, and Lasers|Return to Optical Fibers, Waveguides, and Lasers Menu]]</td>
<td style="text-align: right; width: 33%">[[Planar Dielectric Waveguides|Next Topic]]</td>
</tr>
</table>

Latest revision as of 11:55, 29 December 2009

Previous Topic Return to Optical Fibers, Waveguides, and Lasers Menu Next Topic

Total Internal Reflection

When θ1 > θ1c light can not enter medium n2

A critical concept in the case of optical fibers is the concept of total internal reflection. The bending of light as it goes from one medium into another is related to the index of reflection of the materials (n1 and n2). By Snell's law when n1 > n2 then θ 1 is less than θ2. As you decrease the angle θ1 and bring the light closer to parallel with the interface you reach a critical angle θ1c where there is total internal reflection.

Snells laws are also known as Fresnel's Equations:

<math>\theta _i = \theta _r\,\!</math>

and

<math>\frac {sin \theta_i} {\theta_t} = \frac {n_2} {n_1}\,\!</math>

where

<math>\theta_i\,\!</math> is the angle of incidence
<math>\theta_r\,\!</math> is the angle of reflection
<math>\theta_{c} = sin^{-1}(\frac {n_2} {n_1} )\,\!</math>

where:

<math>\theta_{c}\,\!</math> is the critical angle
<math>n_1 , n_2\,\!</math> are the index of refraction of the two media


if θ1 keeps Increasing: θ2 approaches 90°

for a critical angle Θ1, Θ2 = 90°and the beam emerges along the surface

When

<math>\theta_2 = 90° \rightarrow sin \theta_2 = 1\,\!</math>
<math>\theta_{1c} = sin^{-1} \left (\frac {n_2} {n_1} \right )\,\!</math>


and when

<math>\theta_1 > \theta_{1c}\,\!</math> there is total reflection

In this case there is no transmitted light in the second medium (the irradiance of the reflected and incident beams is equal). Light interacts at the interface and there is a phase shift between the incident and the reflected beams which is dependent on the two materials.

This is a critical process in optical fibers and waveguides because it can carry light for long distances. For these values of index of refraction you get a critical angle of 78.6 which means the light must be very nearly parallel to the interface.

for n1 = 1.53 and n2 = 1.50 : θ1c = 78.6°



Simulations

This flash simulation shows how total internal reflection and minimum radius of turns depends on the diameter of the optical fiber. The diameter changes how much of the light is below the critical angle where it is fully reflected.

<swf width="500" height="400">http://concave.stc.arizona.edu/thepoint/Interactive/ofiber.swf</swf>


This simulation allows you to select combinations of materials with different indexes of refraction. Try to get the best combination to achieve total internal reflection. <swf width="500" height="400">http://concave.stc.arizona.edu/thepoint/Interactive/ofiberapp2.swf</swf>

Previous Topic Return to Optical Fibers, Waveguides, and Lasers Menu Next Topic
Retrieved from "http://cleanenergywiki.org/index.php?title=Total_Internal_Reflection&oldid=5938"