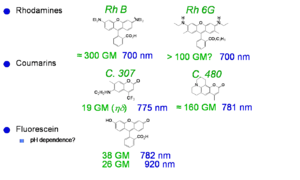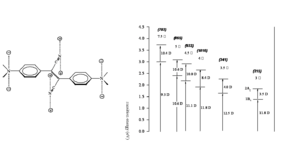Difference between revisions of "Two Photon Absorption"
Cmditradmin (talk | contribs) m (→External Links) |
|||
| (47 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
<td style="text-align: left; width: 33%">[[Introduction to Third-order Processes and Materials |Previous Topic]]</td> | <td style="text-align: left; width: 33%">[[Introduction to Third-order Processes and Materials |Previous Topic]]</td> | ||
<td style="text-align: center; width: 33%">[[Main_Page#Third-order Processes, Materials & Characterization |Return to Third-order Processes, Materials & Characterization Menu]]</td> | <td style="text-align: center; width: 33%">[[Main_Page#Third-order Processes, Materials & Characterization |Return to Third-order Processes, Materials & Characterization Menu]]</td> | ||
<td style="text-align: right; width: 33%">[[ | <td style="text-align: right; width: 33%">[[Characterization of Third-order Materials| Next Topic]]</td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| Line 12: | Line 12: | ||
=== Two-Photon Absorption === | === Two-Photon Absorption === | ||
[[Image:Tpa_energy.png|thumb|300px|A molecule can be excited to state S<sub>2</sub> by absorption of two photons of energy hν<sub>A</sub>.]] | [[Image:Tpa_energy.png|thumb|300px|A molecule can be excited to state S<sub>2</sub> by absorption of two photons of energy hν<sub>A</sub>.]] | ||
Two-photon absorption in a material can be quantified by the two-photon absorption cross section, a quantity that is proportional to the imaginary component of the χ<sup>(3)</sup> tensor (or, on a molecular level, to the imaginary component of γ) and | Two-photon absorption in a material can be quantified by the two-photon absorption cross section, a quantity that is proportional to the imaginary component of the ''χ''<sup>(3)</sup> tensor (or, on a molecular level, to the imaginary component of ''γ'') and depends on the photon energy/energies. In the following we will discuss in detail the case of degenerate (or one-color) two-photon absorption, that is the case where the two photons have the same energy. The figure at right schematically illustrates the degenerate two-photon absorption process, in which two photons, each of energy hν<sub>A</sub>, are simultaneously absorbed and the molecule is excited directly from the ground (S<sub>0</sub>) state to an excited state (state S<sub>2</sub> in the figure) without the formation of an intermediate eigenstate. Neither of the two photons has enough energy to excite the molecule to S<sub>2</sub> by itself, but the sum of the energies of the two corresponds to the energy of state S<sub>2</sub>. The dotted line represents a virtual state (as opposed to an actual eigenstate of the system) that can be thought of as created by the absorption of the first photon and having a very short lifetime (on the order of 10<sup>-15</sup> sec if the photon energy is not in resonance with any electronic transition). If a second photon is absorbed within this lifetime, the two-photon absorption transition occurs and the molecule is excited to S<sub>2</sub>. | ||
[[Image:Tpa_centro.png|thumb|400px|Rate equations and selection rules for two-photon and one-photon absorption.]] | [[Image:Tpa_centro.png|thumb|400px|Rate equations and selection rules for two-photon and one-photon absorption.]] | ||
Once the molecule is in state S<sub>2</sub>, it quickly relaxes by internal conversion to the lowest excited state (S<sub>1</sub> in the figure). From this state, the system can return to the ground state S<sub>0</sub> by emission of fluorescence or by nonradiative decay. Alternatively, an additional photon can be absorbed (bringing the molecule to a higher-lying excited state, S<sub>n</sub>), or electron or energy transfer to another molecule can take place. Typically, once the molecule is in state S<sub>1</sub>, the same set of processes will take place whether the molecule was initially excited into S<sub>2</sub> by two-photon absorption or directly into S<sub>1</sub> by one-photon absorption. For most known materials the two-photon absorption cross section, δ, is small and it is necessary to use intense laser beams in order observe the effects of two-photon absorption. | Once the molecule is in state S<sub>2</sub>, it quickly relaxes by internal conversion to the lowest excited state (S<sub>1</sub> in the figure). From this state, the system can return to the ground state S<sub>0</sub> by emission of fluorescence or by nonradiative decay. Alternatively, an additional photon can be absorbed (bringing the molecule to a higher-lying excited state, S<sub>n</sub>), or electron or energy transfer to another molecule can take place. Typically, once the molecule is in state S<sub>1</sub>, the same set of processes will take place whether the molecule was initially excited into S<sub>2</sub> by two-photon absorption or directly into S<sub>1</sub> by one-photon absorption. For most known materials the two-photon absorption cross section, δ, is small and it is necessary to use intense laser beams in order to observe the effects of two-photon absorption. | ||
The rate equation that describes the formation of the excited state of a molecule by one-photon absorption can we written as follows: | The rate equation that describes the formation of the excited state of a molecule by one-photon absorption can we written as follows: | ||
| Line 22: | Line 22: | ||
where | where | ||
:<math>\sigma\,\!</math> is the one-photon absorption cross section ( | :<math>\sigma\,\!</math> is the one-photon absorption cross section (related to the transition dipole moment of the molecule between the initial and final states of the transition) | ||
:<math>N_{GS}\,\!</math> is the number of molecules per unit volume in the ground state | :<math>N_{GS}\,\!</math> is the number of molecules per unit volume in the ground state | ||
:<math>N_{OP}\,\!</math> is the number of molecules per unit volume in the excited state due to one-photon absorption | :<math>N_{OP}\,\!</math> is the number of molecules per unit volume in the excited state due to one-photon absorption | ||
| Line 32: | Line 32: | ||
In a similar manner, the rate equation for two-photon absorption can be written as follows, keeping in mind that two photons are needed to produce one excited molecule (in the reaction analogy, the reaction is now second-order in the photon flux, but still first-order in the concentration of molecules): | In a similar manner, the rate equation for two-photon absorption can be written as follows, keeping in mind that two photons are needed to produce one excited molecule (in the reaction analogy, the reaction is now second-order in the photon flux, but still first-order in the concentration of molecules): | ||
:<math>\frac {dN_{TP}} {dt} = \frac {1}{ 2} \delta N_{GS} F^2\,\!</math> | :<math>\frac {dN_{TP}} {dt} = \frac {1}{ 2} \delta N_{GS} F^2\,\!</math> | ||
where | where | ||
| Line 43: | Line 43: | ||
== Advantages of TPA == | == Advantages of TPA == | ||
Two photon absorption is considered to be a nuisance in the case of all-optical switching using χ<sup>(3)</sup> materials because it causes attenuation of the light beam and damage to the material can result from severe heating of samples. However the two-photon absorption process can be exploited in another contexts, apart from being of interest in the study of fundamental spectroscopic properties of materials. | Two-photon absorption is considered to be a nuisance in the case of all-optical switching using ''χ''<sup>(3)</sup> materials because it causes attenuation of the light beam and damage to the material can result from severe heating of samples. However the two-photon absorption process can be exploited in another contexts, apart from being of interest in the study of fundamental spectroscopic properties of materials. | ||
<br clear='all'> | <br clear='all'> | ||
=== Two-Photon Processes Provide 3-D Resolution === | === Two-Photon Processes Provide 3-D Resolution === | ||
[[Image:Tpa_cuvette_3D.png|thumb|400px|Two laser beams are focused in a sample molecule in solution inside a cuvette; the top | [[Image:Tpa_cuvette_3D.png|thumb|400px|Two laser beams are focused in a sample molecule in solution inside a cuvette; the top beam is tuned at a wavelength at which two-photon absorption can take place, the bottom one at a different wavelength that can excite the molecules by one-photon absorption. The blue light visible in the photograph is the fluorescence emitted by the molecules after excitation.]] | ||
If a light beam is focused into sample at a wavelength suitable for one-photon absorption, molecules are excited throughout the beam path in the sample, as evidenced by the fluorescence emission in the bottom part of the cuvette at right. If the beam is tuned at a wavelength at which the material exhibits two-photon absorption, only the molecules located very close to the focus of the laser beam are excited (top beam in the photograph). This is related to the fact that the excitation rate depends on the square of the light intensity, as discussed above, and that in a focussed beam the light intensity is maximum at the focal plane and decreases approximately with the square of the distance from the focal plane, ''z'', | If a light beam is focused into sample at a wavelength suitable for one-photon absorption, molecules are excited throughout the beam path in the sample, as evidenced by the fluorescence emission in the bottom part of the cuvette at right. If the beam is tuned at a wavelength at which the material exhibits two-photon absorption, only the molecules located very close to the focus of the laser beam are excited (top beam in the photograph). This is related to the fact that the excitation rate depends on the square of the light intensity, as discussed above, and that in a focussed beam the light intensity is maximum at the focal plane and decreases approximately with the square of the distance from the focal plane, ''z'', along the propagation direction (because the area of the beam increases moving away from the focus). Overall, the excitation rate for TPA and the intensity of the two-photon induced fluorescence decrease as the forth power of the distance from the focal plane. Consequently, in the solution in the figure the two-photon induced fluorescence is strongest at the beam focus and its intensity drops off very quickly on either side of the focal plane, resulting in what looks like emission from a "single point" (or small volume) in the solution. At the diffraction limit, the TPA excitation is confined to a volume on the order of the cube of the wavelength of the excitation light. Most of the applications of TPA are based on this ability to confine and control the excitation volume in a material with good resolution in three dimensions, as any excited state process that can take place in the material after two-photon excitation (such as fluorescence emission or energy transfer) will be confined to the same small volume. | ||
=== TPA Processes Provide Improved Penetration of Light Into Absorbing Materials === | === TPA Processes Provide Improved Penetration of Light Into Absorbing Materials === | ||
[[Image:Tpa_cuvette_penetrate.png|thumb|400px| | [[Image:Tpa_cuvette_penetrate.png|thumb|400px|One-photon absorption (bottom): a light beam from the right is quickly absorbed by a concentrated solution of a fluorescent material. Two-photon absorption (top) the beam is able to penetrate the solution without being attenuated until the focus of the beam; only near the focus the light intensity is high enough to activate two-photon induced fluorescence.]] | ||
In a | In the figure at right the same two beams as in the case above are focused in a solution of a fluorescent compound, but now the solution is much more concentrated. It can be seen that for the bottom beam (one-photon absorption case) fluorescence emission can be seen only close to the right wall of the cuvette, as the beam is strongly absorbed and attenuated by the solution (the beam is propagating from right to left). Thus the penetration depth of the beam in the solution is small. In the case of the top beam, there is no one-photon absorption and two-photon absorption only occurs near the focus of the beam (in this case the center of the cuvette), so that there is no beam attenuation before the beam reaches the focus and the laser beam can penetrate farther into a sample with respect to the one-photon absorption situation. The ability to penetrate a material and to be focused accurately in three dimensions make the TPA process ideal for fluorescence imaging of thick samples (even in vivo) or in medical applications in which, for example, a drug can be activated by TPA at a very precise location without affecting the tissue above and below the focal plane of the excitation beam. | ||
<br clear='all'> | <br clear='all'> | ||
== | == Measuring the Two-Photon Absorption Cross Section == | ||
[[Image:Tpa_measurement.png|thumb|400px|Schematic of an optical setup for a two-photon induced fluorescence experiment. The red line represents the excitation beam, the blue line is the two-photon induced fluorescence, the dashed line is a beam splitter and the solid black lines are filters (to control the beam intensity or to block the excitation beam before the PMT detectors).]] | |||
One of the techniques used to measure the TPA cross section of a material is based on two-photon induced fluorescence. In this measurement, a laser beam is propagated through the sample of interest (the beam can be focused or collimated) and the fluorescence light that is emitted by the excited molecules after two-photon absorption is collected and measured by a detector (for example a photomultiplier tube, PMT). As seen above, the number of molecules excited by two-photon absorption per unit time and volume, ''N''<sub>TP</sub>, is proportional to the TPA cross section of the material at that excitation wavelength, the concentration of molecules and the square of the photon flux. The number of fluorescence photon emitted by these molecules is then: | |||
= | :<math>n_{fl} = \eta N_{TP}\,\!</math>, | ||
'' | where ''η'' is the fluorescence quantum yield of the material. | ||
Thus, the intensity of the two-photon induced fluorescence is proportional to the TPA cross section ''δ''. This technique can be used for absolute or relative measurements of TPA cross sections. In the absolute case, all the relevant parameters (such as the instantaneous photon flux and the detection efficiency of the optical setup) need to be measured independently. In relative measurements, an unknown compound is analyzed under the same conditions as a material of known TPA cross section. | |||
The figure at right shows an example of optical setup that can be used for TPA cross section measurements. A tunable laser is needed to measure the TPA spectrum, as the TPA cross section depends on the excitation wavelength. In this example, the laser beam is split in two by a beam splitter and one of arm is used as reference for the intensity of the beam, to correct for fluctuations in intensity from pulse to pulse during the course of the measurement. | |||
* | '''Measurement Considerations:''' | ||
* A pulsed laser is needed (pulse durations in the ns, ps, fs range can be used). | |||
* | * The laser need to be tunable to obtain spectral information on the material. | ||
* The two-photon fluorescence method is applicable only to fluorescent materials (the z-scan technique can be used for fluorescent and non-fluorescent materials). | |||
* | |||
* | * The detection of the fluorescence emission can be done in various configurations (90º collection, backward scattering, forward scattering, ...); scattering of the excitation beam by the sample needs to be removed from the fluorescence signal before detection (for example using filters or monochromators). | ||
* The dependence of the two-photon induced fluorescence signal on the square of the laser beam intensity needs to be tested for the actual experimental conditions used, to exclude contributions from other effects. | |||
* Possible reasons for deviation from the dependence on the square of the laser intensity: linear absorption, stimulated emission, ground state depletion, ... | |||
* Importance of spatial and temporal profile of the excitation beam. | |||
See equipment video on [[Two-Photon Spectroscopy]] | See equipment video on [[Two-Photon Spectroscopy]] | ||
== Calculation of TPA Cross Sections == | |||
=== Perturbative Expression for γ, as Relevent to Two-Photon Absorption === | === Perturbative Expression for γ, as Relevent to Two-Photon Absorption === | ||
The perturbative expression for gamma can be | The perturbative expression for the hyperpolarizability ''γ'' for the frequency component relevant to two-photon absorption can be written as follows (under the assumption that the system can be described by the so-called "three level model", in which only the ground state, ''g'', the lowest excited state, ''e'', and a higher-lying two-photon allowed state, ''e''', are considered): | ||
:<math>\gamma( -\omega; \omega, -\omega, \omega) \propto \frac{ M^2_{ge} \Delta \mu^2_{ge}} {(E_{ge} - | :<math>\gamma( -\omega; \omega, -\omega, \omega) \propto \frac{ M^2_{ge} \Delta \mu^2_{ge}} {(E_{ge} - \hbar \omega - i \Gamma_{ge})^2(E_{ge}-2\hbar \omega -i \Gamma_{ge})} + \frac {M^2_{ge} M^2_{ee^{\prime}}} {(E_{ge} - \hbar \omega- i \Gamma_{ge})^2 (E_{ge^{\prime}} - 2 \hbar \omega - i\Gamma_{ge^{\prime}})}\,\!</math> | ||
where: | |||
:<math>M_{ge} \,\!</math> is the transition dipole moment between states ''g'' and ''e'' | |||
:<math>M_{ge^{\prime}} \,\!</math> is the transition dipole moment between states ''g'' and ''e''' | |||
:<math> \Delta \mu_{ge} \,\!</math> is the difference between the dipole moment of states ''g'' and ''e'' | |||
:<math>E_{ge} \,\!</math> and <math>E_{ge^{\prime}} \,\!</math> are the energies for the transitions between the subscripted states | |||
:<math> \omega \,\!</math> is the angular frequency of the excitation beam and | |||
:<math> \Gamma \,\!</math> are damping terms. | |||
For a centrosymmetric molecule | For a centrosymmetric molecule <math>\Delta \mu_{ge}\,\!</math> goes to zero (the dipole moment is zero in both ''g'' and ''e'' states) so that the first term in the equation for ''γ'' goes to zero. For non centrosymmetric molecules both terms contribute to the hyperpolarizability. | ||
From the equation above it can be seen that two-photon resonances can occur when the photon energy is such that: <math> 2 \hbar \omega = E_{ge} \,\!</math> or <math> 2 \hbar \omega = E_{ge^{\prime}} \,\!</math> | |||
The TPA cross section (δ ) | The TPA cross section (''δ'') is proportional to the imaginary component of ''γ'': | ||
:<math>\delta(\omega) = \frac { | :<math>\delta(\omega) = \frac {4\pi^2 \hbar \omega^2} {n^2c^2} L^4 Im \gamma( -\omega; \omega, -\omega, \omega)\,\!</math> | ||
The above equation is valid in the cgs system of units; <math> n\,\!</math> is the refractive index of the material, <math> L\,\!</math> is the local field factor (which depends on the refractive index), and <math> c\,\!</math> is the speed of light. | |||
=== | === Calculations of the TPA Cross Section in a Donor-Acceptor Molecule=== | ||
[[Image: | [[Image:Tpa_donaracceptor.png|thumb|300px|TPA calculations for stilbene.]] | ||
A simple donor/acceptor stilbene with an amino group and a formyl group on the phenyl rings in para position has been used a model compound for calculations of the TPA cross section. The figure at right shows the molecule in two resonance structures and the calculated TPA cross section as a function of the bond order alternation (BOA; i.e. the difference between the bond order in adjacent CC bonds in the vinylene bridge), which changes going from one resonance structure to the other. The value of ''δ'' for the transition from the ground to the first excited state (S<sub>0</sub> to S<sub>1</sub>, left plot) is small for large negative values of the BOA (corresponding to the resonance structure on the left side), reaches a maximum when the BOA increases, and then it goes to zero when the BOA approaches the cyanine limit (BOA = 0). The same trend as a function of BOA is obtained for the change in dipole moments (see inset). | |||
The TPA cross section for the transition to the second excited state (S<sub>0</sub> to S<sub>2</sub>, right plot) exhibits a more complicated behavior as a function of BOA and multiple peaks are present, in part because of changes in the detuning term <math>E_{ge} - \hbar \omega\,\!</math>. When the energy for the transition to S<sub>1</sub> is very close to half of the energy for the transition to S<sub>2</sub>, the detuning term becomes small and ''δ'' increase; this situation is referred to a "double resonance". | |||
See T. Kogej et.al. Chem. Phys. Lett. 1998, vol. 298, p. 1 <ref>T. Kogej et.al. Chem. Phys. Lett. 1998, 298, 1.</ref> | |||
== Examples of Two-Photon Absorbing Materials == | |||
=== Two-Photon Absorption Spectrum of a Centrosymmetric Molecule === | |||
[[Image:Tpa_spectra.png|thumb|400px|Two-photon and linear absorption spectra of the molecule shown (in toluene solutions).]] | |||
In | Here is a centrosymmetric molecule with a conjugated backbone and donor groups on both ends. The energy level diagram on the left side of the figure, similar to that discussed at the beginning of the section, shows the allowed transitions for this molecules. There can be one-photon excitation into S<sub>1</sub> (this transition is not two-photon allowed because the molecule is centrosymmetric) and two-photon excitation into S<sub>2</sub> (again for symmetry reason this transition is not one-photon allowed). After excitation, rapid relaxation can occur by internal conversion back to S<sub>1</sub> and then fluorescence emission from S<sub>1</sub>. There is no fluorescence emission from S<sub>2</sub> because, in most cases, the relaxation from S<sub>2</sub> to S<sub>1</sub> is much faster than the fluorescence lifetime. In centrosymmetric molecules this can be easily understood, because the transition from S<sub>2</sub> to S<sub>0</sub> is symmetry forbidden for one photon, therefore the transition dipole moment for this transition is close to zero and the coupling between the ground and the excited state is very small, resulting in a long radiative lifetime of the excited state. However even if the molecule was not centrosymmetric, the internal conversion relaxation from a higher-lying excited state is generally so fast that there still would not be fluorescence from S<sub>2</sub> (or S<sub>n</sub>). This is known as "Kasha's rule", which was described by Michael Kasha and which states that, irrespective of the electronic state of the molecule reached by excitation, fluorescence will only occur from the lowest lying excited state (S<sub>1</sub>). Most molecules behave according to Kasha's rule, but a few exceptions are known, such as azulene. | ||
The figure also shows the one-photon (blue line) and two-photon absorption (red line) spectra of the molecule and the fluorescence emission spectrum (green line). | |||
In the graph note that the photon energy of the TPA band is lower (longer wavelength; the horizontal axis represent the wavelength of the excitation beam) than the one-photon absorption band (blue line) and of the fluorescence (green line). The TPA peak is around 720 nm, for this molecule. As two photons are involved in the transition, a TPA peak at 720 nm corresponds to a "transition wavelength" of 720 nm / 2 = 360 nm. The peak for linear absorption to S<sub>1</sub> is 430 nm. This shows that the state reached by two-photon absorption is higher in energy than the S<sub>1</sub> state and that there is very little one-photon absorption in this range (the small absorption seen at 360 nm is due to vibronic sub-levels of S<sub>1</sub>), consistent with the selection rules described earlier for centrosymmetric molecules. | |||
=== Laser | see Rumi et al., J. Am. Chem. Soc. 2000, vol. 122, p. 9500 <ref>Rumi et al., JACS 122, 9500, 2000</ref> | ||
=== Laser Dyes === | |||
[[Image:Tpa_laserdyes.png|thumb|300px|]] | [[Image:Tpa_laserdyes.png|thumb|300px|]] | ||
Xu and Webb measured the cross section for laser dyes | Xu and Webb measured the TPA cross section for various laser dyes and other commercially available compounds. The values at the peak of the two-photon absorption band for a selection of these compounds are reported at right. The TPA cross section is given here in goeppert-mayer (GM) units: 1 GM = 1 × 10<sup>-50</sup> cm<sup>4</sup> s molecules<sup>−1</sup> photon<sup>−1</sup>. The unit is named in honor of Maria Goeppert Mayer, the German physicist that predicted the process of two-photon absorption in 1931. TPA was not actually observed experimentally until the early 60s, when lasers were developed that had sufficient intensity to lead to measurable effects in materials. | ||
One dye shown here has a cross section of about 300 GM, the other are in the range 10-100 GM. | |||
See Xu and Webb <ref>C. Xu, JOSA B, 1996;</ref> Albota 1998 <ref>M. Albota, Appl. Opt., 1998;</ref>Fisher 1998 <ref>W. G. Fisher, Appl. Spectr., 1998.</ref> | See Xu and Webb, J. Opt. Soc. Am. 1996, vol. 13, p. 481; <ref>C. Xu, JOSA B, 1996;</ref> Albota et al., Appl. Opt. 1998, vol. 37, p. 7352; <ref>M. Albota, Appl. Opt., 1998;</ref> Fisher et al., Appl. Spectrosc. 1998, vol. 52, p. 536. <ref>W. G. Fisher, Appl. Spectr., 1998.</ref> | ||
<br clear='all'> | <br clear='all'> | ||
=== Vagaries of | === Vagaries of TPA Measurements: The “famous” AF-50 === | ||
[[Image:Tpa_af50.png|thumb|500px| | [[Image:Tpa_af50.png|thumb|500px|Values of δ for compound AF-50 (structure shown) from various measurements reported in the literature. τ is the pulse duration used.]] | ||
The chart shows various measurements for the molecule AF-50. | The chart shows various measurements of the TPA cross section for the molecule AF-50. It can be seen that the values vary over many orders of magnitude. What is the reason for these differences? Is the problem intrinsic in the material or due to the way in which the parameter was measured? The measurements were indeed made using various techniques and conditions. The quantity ''δ'' is a molecular characteristic and it should not depend on the experimental conditions and optical set-up used. The variation in value in the chart is in part indicative of the measurement problems in the NLO field in general, as these are affected by relatively large uncertainties under the best of circumstances. In the case of TPA absorption, though, there can be additional problems, because some experimental techniques may not be selective to measure only TPA and for certain intensity ranges and pulse duration other effect may contribute to the observed signal. For example, the experiment that gave a ''δ'' value of 11560 GM was based on the nonlinear transmission (NLT) technique and conducted using pulses with duration of a few nanoseconds. It is now recognized that for pulse duration this long, many materials exhibit other nonlinear absorption processes in addition to TPA, in particular there can be excited state absorption (ESA) from S<sub>1</sub> to a higher state S<sub>n</sub>, if the population of S<sub>1</sub> becomes large enough. During the NLT measurement the combined effect of TPA and ESA is seen and results in an apparent TPA cross section that is very large. This is, however, not the "intrinsic" cross section of the material, but an "effective" cross section that depends on the excitation conditions used in the experiment. While this is detrimental for the measurement of the "intrinsic" cross section, the large magnitude of the "effective" cross sections in some materials could be useful, for example, in making coatings for safety glasses that could exclude high intensity laser light (i.e. to achieve "optical limiting"). | ||
<br clear='all'> | <br clear='all'> | ||
=== | === Initial Observations on a Bis-Donor Stilbene === | ||
[[Image: | [[Image:Tpn_bisdonorstilbene.png|thumb|300px|Bis-donor substituted stilbene.]] | ||
A stilbene derivative (BDAS) with two π-donor groups (dibutyl amino group) is an instructive molecule to study. | |||
'''Evidence for two-photon absorption''' | '''Evidence for two-photon absorption''' | ||
*Strong blue fluorescence was observed when pumped with orange laser light | |||
*Fluorescence intensity for pumping with orange light depends on I<sup>2</sup> | |||
*Strong blue fluorescence when pumped with orange light | *Strong nonlinear transmission was observed (that is the transmittance of the material changes as a function of the intensity of the excitation laser beam) | ||
*Fluorescence depends on I<sup>2</sup> | |||
* | |||
For this compound, the maximum TPA cross section (at 600 nm), ''δ'' was measured to be 210 x 10<sup>-50</sup> cm<sup>4</sup> s/photon, while for stilbene (i.e. if the two donor groups are removed) δ = 12 x 10<sup>-50</sup> cm<sup>4</sup> s/photon. | |||
Thus, the TPA cross section of BDAS is about 20 times that for the molecule without the electron donor groups. ''δ'' for BDAS is very large and it is useful to understand why the donors have this effect. | |||
'''Interesting features for two-photon applications''' | '''Interesting features for two-photon applications''' | ||
*High fluorescence quantum yield, φ<sub>fl</sub> ~ 0.9 | *High fluorescence quantum yield, φ<sub>fl</sub> ~ 0.9 | ||
*High optical transmission | *High optical transmission at low intensity | ||
*Low oxidation potential, | *Low oxidation potential, E<sub>D<sup>+</sup>/D</sub> = + 0.035 V vs. Fc/Fc<sup>+</sup> (this compound is very easy to oxidize in the ground state and is a powerful reducing agent in the excited state) | ||
=== Proposed Model to Enhance TPA Cross Sections in Symmetrical Molecules === | === Proposed Model to Enhance TPA Cross Sections in Symmetrical Molecules === | ||
[[Image:Tpn_bisdonorstilbene_symm.png|thumb|300px|]] | [[Image:Tpn_bisdonorstilbene_symm.png|thumb|300px|]] | ||
Theoretical calculations can help to explain | Theoretical calculations can help to explain the properties of the BDAS molecule. | ||
BDAS has large and symmetrical charge transfer from nitrogens (becoming more positive) to | Calculations show that BDAS has large and symmetrical charge transfer from nitrogens (becoming more positive) to the vinyl group in the middle (becoming more negative) when the molecule is excited from S<sub>0</sub> (''g'') to S<sub>1</sub> (''e'') and to S<sub>2</sub> (''e''') and this charge transfer is reflected primarily in very a large transition dipole moment between S<sub>1</sub> and S<sub>2</sub> (<math>M_{ee^{\prime}}\,\!</math>). The value of <math>M_{ee^{\prime}}\,\!</math> is much smaller in the case of stilbene. | ||
These results suggest that a large change in quadrupole moment between S<sub>0</sub> and S<sub> | These results suggest that a large change in quadrupole moment between S<sub>0</sub> and S<sub>2</sub> can lead to large values of ''δ''. | ||
<br clear='all'> | <br clear='all'> | ||
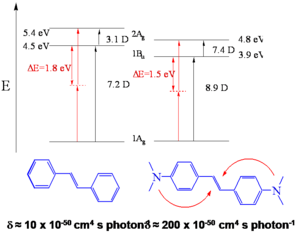
'''Bis Donor Substitution''' | '''Effect of Bis-Donor Substitution''' | ||
[[Image:Tpn_bisdonorstilbene_subst.png|thumb|300px| Transition energies and transition dipole moments for stilbene and a bid-donor stilbene obtained from quantum-chemical calculations]] | |||
The observation above suggests certain design strategies for increasing the dipole or quandrupole moment: if you want to make the dipole (or quadrapole) moment larger you can increase the distance over which charge is separated and you can increase the charge that is separated by that distance, or do both. The first would correspond to increasing the length of the molecule, the second to introducing functional groups that can facilitate the charge transfer. This is the role that the dibutylamino groups play in BDAS with respect to stilbene. | |||
This interpretation is supported by results of quantum chemical calculations performed on these molecules (in the calculations, dimethyl- instead of dibutyl-amino groups were considered). | |||
The transition dipole moment between the ground and first excited state is 7.2 D for stilbene and 8.9 D for BDAS. The biggest change, though, is observed for <math>M_{ee^{\prime}}\,\!</math>, as the transition dipole goes from 3.1 D in stilbene to 7.4 D for BDAS. | |||
A simplified expression for the maximum TPA cross section for the transition to ''e''' in centrosymmetric molecules can be obtained from the three-level equation given earlier for ''γ'' (keeping in mind that δ is proportional to Im ''γ''): | |||
:<math>\delta_{ | :<math>\delta_{g \rightarrow e^{\prime}} \propto \frac {M^2_{ge} M^2_{ee^{\prime}}} {(E_{ge} - \hbar \omega )^2 \Gamma_{ge^{\prime}}} \,\!</math> | ||
The term <math>M_{ee^{\prime}}\,\!</math> is squared in the equation and it can be seen that an increase in the value of this parameter from stilbene with respect to BDAS is the reason for the very high TPA cross section for BDAS. | |||
'''Transition Dipole Moments''' | |||
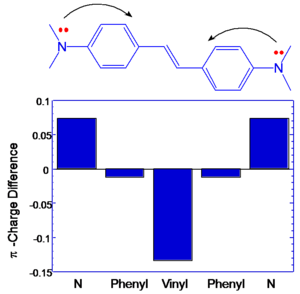
[[Image:Tpa_transdip_densities.png|thumb|300px| Change in atomic charges for the transition from ''g'' to ''e'' for stilbene and a bis-donor stilbene.]] | |||
If the components that contribute to transition dipole moments are located farther from the middle of the molecule the contribution to the transition dipole moment is correspondingly larger. This is illustrated at right, where the change in charge distribution is plotted for the various atoms in the molecules. It can be seen that in BDAS one of the largest changes occurs on the nitrogens, which are located at the opposite ends of the molecule. This change, coupled with the extended distance from the molecular origin results in a large transition dipole moment for this molecule. In stilbene, the charge distribution changes mostly in the central part of the molecule, resulting in a smaller transition dipole moment <math>M_{ee^{\prime}}\,\!</math> . | |||
[[Image: | There is an optimal amount of charge transfer that is needed to get the largest cross section. | ||
[[Image:Tpa transdip boa.png|thumb|300px|Transition dipole moment and transition energy ]] | |||
<br clear='all'> | <br clear='all'> | ||
== | === Optical Limiting via Two-Photon Absorption in Bis-Donor Stilbene === | ||
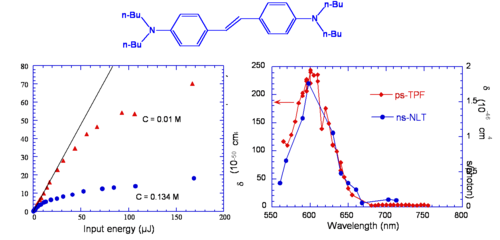
[[Image: | [[Image:Tpn_limiting_bisdonorstilbene.png|thumb|500px|Left: Output energy vs input energy for two solutions of BDAS excited at 600 nm with nanosecond pulses. Right: Spectra obtained from two-photon fluoresence with ps pulses (ps-TPF) and nonlinear transmission with nanosecond pulses (ns-NLT). ]] | ||
It was mentioned above that nonlinear transmission was observed in BDAS. This material behaves as a good optical limiter for nanosecond pulses (see plot on the left side of the figure, for two different concentrations). This is due to the fact that the TPA cross section of this molecule is large, as seen above, and that this molecule also has a large excited state absorption cross section; when the molecule is excited with nanosecond pulses at a wavelength between 550 and 650 nm, a cascade of TPA and ESA processes takes place, resulting in large attenuation of the incident beam (optical limiting). The plot on the right side of the figure displays the TPA cross section of the compound obtained from a two-photon induced fluorescence measurement (ps-TPF, shown in red) and the nonlinear transmission spectrum (ns-NLT, shown in blue), that is the values of "effective" TPA cross section obtained from a NLT experiment with ns pulses: the two curves are similar in shape, but the scales of cross sections are different. The ns-NLT scale has units of 10<sup>-46</sup> cm<sup>4</sup> s/photon and the ps-TPF spectrum is on the scale of 10<sup>-48</sup> cm<sup>4</sup> s/photon, a factor of 100 difference. This is another example of the fact that NLT measurement performed with long pulse durations yield only the "effective" TPA cross section, which involves two-photon absorption followed by excited state absorption, as opposed to the "intrinsic" TPA cross section, which can be obtained from two-photon induced fluorescence measurements or other techniques that allow to exclude the effect of ESA (such as z-scan measurements with fs pulses at moderate peak intensities of the laser beam). | |||
<br clear='all'> | <br clear='all'> | ||
=== Transition Dipole Moments === | == Design of TPA Chromophores == | ||
=== Three-Level Model and Transition Dipole Moments === | |||
[[Image:Tpa_trans_dipole.png|thumb|400px|]] | [[Image:Tpa_trans_dipole.png|thumb|400px|]] | ||
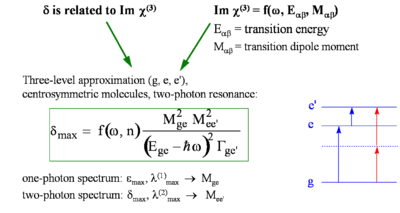
We summarize here the expression for ''δ'' as a function of molecular parameters for a centrosymmetric molecule within the three-level model approximation and discuss how this can be used to derive guidelines for the design of chromophores with large TPA cross section: | |||
:<math>\delta _{max} = f(\omega, n) \frac {M^2_{ge} M^2 _{ee^{\prime}}} {(E_{ge} - \hbar\omega)^2 \ | :<math>\delta _{max} = f(\omega, n) \frac {M^2_{ge} M^2 _{ee^{\prime}}} {(E_{ge} - \hbar\omega)^2 \Gamma_{ge^\prime}}\,\!</math> | ||
where: | where: | ||
:<math>\delta_{max}\,\!</math> is the cross sections | :<math>\delta_{max}\,\!</math> is the cross sections at the peak of the TPA band (i.e. for <math>\hbar \omega\,\!</math> = <math> (1/2) E_{ge^{\prime}}\,\!</math>). | ||
:<math>M_{\alpha\beta}\,\!</math> is the transition dipole moment for two levels α | :<math>M_{\alpha\beta}\,\!</math> is the transition dipole moment for two levels α and β | ||
:<math>E_{\alpha\beta}\,\!</math> is the energy | :<math>E_{\alpha\beta}\,\!</math> is the energy difference between levels α and β | ||
:<math>\hbar \omega\,\!</math> is the photon energy | :<math>\hbar \omega\,\!</math> is the photon energy. | ||
:<math>\ | :<math>\Gamma_{ge^{\prime}}\,\!</math> is the damping term (typically on the order of 0.1 eV) | ||
In summary | In summary: | ||
:<math>\delta_{ | :<math>\delta_{max} \propto M^2_{ge} M^2_{ee^\prime} \Delta E^{-2}\,\!</math> | ||
where <math>\Delta E\,\!</math> is the detuning energy: <math>\Delta E\ = E_{ge} - \hbar \omega \,\!</math> | |||
[[Image:Tpa_chromophores.png|thumb|300px|Molecular structure and value of δ (in GM units) for series of compounds with different substitution patters.]] | |||
This suggests that to obtain large ''δ'' values, one of the following strategies can be used, at least in the case of centrosymmetric molecules, to increase the magnitude of one or both transition dipole moments: | |||
*Increase the distance between the donors, so as to increase the distance over which the charge is transferred. | |||
*Increase the strength of the donors, so as to increase the amount of charge that is transferred. | |||
*Add acceptors to the middle of molecule, to further increase the amount of charge transfer. | |||
*Flip the relative position of donors and acceptors in the molecule, using donors in the center and acceptors on the ends. | |||
The diagram reports the TPA cross section (numbers under the molecular structures, in GM units) for a series of molecules with phenylene-vinylene conjugated backbones, to show the effect of donors (shown in blue) and acceptors (shown in red), as well as longer molecular chain lengths. The trend observed for ''δ'' in these compounds is consistent with the expectations based on the three-level model. The combination of these design strategies allows to achieve cross section on the order of thousands of GM. The trend in cross section when the molecular structure is changed are further illustrated in the following two sub-sections. | |||
<br clear='all'> | |||
=== Chain-Length Dependence === | |||
[[Image:Tpa_chainlength.png|thumb|300px|TPA spectra for molecules with different conjugation lengths.]] | |||
The graph shows that as the length of the conjugated bridge increases, the energy of the two-photon absorption band decreases (the maximum in TPA band shifts to longer wavelength) and the magnitude of the TPA cross section increases, due to the increase of the transition dipole moment <math>M_{ge}\,\!</math>. | |||
<br clear='all'> | |||
=== Effect of D/A Substitution === | === Effect of D/A Substitution === | ||
[[Image:Tpa_donaracceptor_substitute.png|thumb|300px|Trends for dipole moments of quadrupolar molecules]] | [[Image:Tpa_donaracceptor_substitute.png|thumb|300px|Trends for ''δ'', detuning energy, and transition dipole moments of a series of quadrupolar molecules.]] | ||
The table shows that by making these molecules quadrupolar, that is attaching electron-donating and/or electron-withdrawing functional groups on the conjugated backbone in a centrosymmetric arrangement, the TPA cross section increases significantly with respect to molecules without substituents. This is mainly due to the increase in the transition dipole moment <math>M_{ee^\prime}\,\!</math>: in fact this parameter is much larger in the molecule with donors at the termini of the molecule (second row in the table), than the one without donors (first row); the transition moment becomes even larger when the molecules contains both donor and acceptor groups (last three rows). | |||
<br clear='all'> | <br clear='all'> | ||
== Applications for TPA == | == Applications for TPA == | ||
=== Two- | === Two-Photon Initiated Polymerization and 3D Microfabrication === | ||
[[Image:Tpa_crosslinked.png|thumb|300px|TPA can be used to stimulate cross linking in a polymer.]] | [[Image:Tpa_crosslinked.png|thumb|300px|TPA can be used to stimulate cross linking in a polymer.]] | ||
Two photon absorption can be used to initiate polymerization on a precise microscopic scale. A beam can be focused at | Two-photon absorption can be used to initiate photo-polymerization on a precise microscopic scale in 3D. A beam can be focused at a desired position in a polymer precursor, an initiator in the precursor is excited by two-photon absorption, photoactivating the polymerization or cross-linking in the material. This process is confined to the vicinity of the excitation volume. When the laser beam is moved to a different position, the polymerization or cross-linking is initiated in the new location. Then the non-crosslinked portions (those that have not been exposed to the laser beam) can be washed away by a solvent. This process can be used for microfabrication, that is the fabrication of a polymeric structure at the microscale with good control of the feature sizes in three dimensions, by scanning the laser beam in a prescribed pattern. This process has been used to fabricate structures in various types of resins and high degree of complexity. Selected example can be found in the following publications: | ||
Wu et al., Proc. SPIE, 1992, vol. 1674, p. 776 <ref>E. S. Wu, J. H. Strickler, W. R. Harrell & W. W. Webb, SPIE Proc. 1674, 776 (1992)</ref> | |||
Maruo et al., Opt. Lett., 1997, vol. 22, p. 132 <ref>S. Maruo, O. Nakamura & S. Kawata, Opt. Lett. 22, 132 (1997)</ref> | |||
[http://www.nature.com/nature/journal/v412/n6848/full/412697a0.html "Micro bull"] | Cumpston et al., Nature 1999, vol. 398, p. 51 [http://www.nature.com/nature/journal/v398/n6722/full/398051a0.html] | ||
Kawata et al., Nature 2001, vol. 412, p. 697 [http://www.nature.com/nature/journal/v412/n6848/full/412697a0.html "Micro bull"] | |||
[http://spie.org/x19493.xml?ArticleID=x19493 "Thinking man"] | [http://spie.org/x19493.xml?ArticleID=x19493 "Thinking man"] | ||
=== Two-Photon Initiators with Enhanced Sensitivity === | |||
[[Image:Tpa initiators.png|thumb|300px|New dyes increase the effective range of power where 3D "writing" can occur | [[Image:Tpa initiators.png|thumb|300px|New dyes increase the effective range of power where 3D "writing" can occur.]] | ||
Regular photo-initiators are not excellent two photon absorbers. | Regular photo-initiators are not excellent two-photon absorbers. A femtosecond laser can supply a beam with very large power and thus it may be possible, in some cases, to use them as initiators under two-photon excitation conditions. However, at this laser power damage to the material could occur. At the same time, if the laser power is too low, the microscopic structure obtained by the photopolymerization may not have sufficient mechanical strength after removal of the unexposed resin, or the process may not be reliable enough. To achieve good reliability and fidelity in the microfabrication process it is desirable to utilize photoinitiators that are efficient and that have a wide dynamic range in writing power. For conventional initiators used under two-photon excitation conditions, the writing power range (that is the ratio between the power at which damage starts occurring and the minimum power that gives well-formed structures) is usually small, for example it is between 1 and 2.5 for the first three initiators in the table at right. Newly developed two-photon absorbing dyes expand this range, up to a value of 50 for the bottom two examples in the table. This increase results mainly from the fact that these dyes have a much larger TPA cross section than conventional initiators. This lets you write more accurately and faster because the beam does not have remain in the same place as long. The figures are SEM images of the same nominal structure fabricated: below the writing threshold, resulting in an incomplete structure after removal of the unexposed resin (top image), within the writing power range (middle image), and above the damage threshold of the material (bottom image). | ||
<br clear='all'> | <br clear='all'> | ||
=== Fluorescent and Refractive Bit Optical Data Storage === | === Fluorescent and Refractive Bit Optical Data Storage === | ||
[[Image:Tpa_optical_storage.png|thumb|300px|Fluorescent and Refractive Bit | [[Image:Tpa_optical_storage.png|thumb|300px|Fluorescent and Refractive Bit Optical Data Storage.]] | ||
This technique can be used to | This two-photon induced polymerization technique can be used in optical data storage applications. For example the compound shown at right is non-fluorescent, but it becomes fluorescent when the pendant acrylate groups are incorporated in an acrylate polymer. When this compound is mixed with other acrylate monomers and exposed to laser light at an appropriate wavelength and intensity, TPA-induced polymerization takes place and the resulting polymer is fluorescent. The resin in the unexposed areas remains non-fluorescent. The image at the bottom left shows two rows of fluorescent bits, obtained by two-photon induced polymerization, on the dark background of the unexposed resin. | ||
After laser exposure, the polymer also has higher density, due to cross-linking, than the unexposed portions of the resin. If the density goes up and the polarizability of the material stays the same, the susceptibility goes up and the refractive index goes up. Thus, it is also possible to "read" the bits based on the contrast in refractive index. Peter Rentzepis at the UC Urvine is using this method to create a 3D optical memory. | |||
Because of the three-dimensional confinement of the excitation volume that is characteristic of the TPA process, it is possible to write and read sets of bits in multiple layers within the material, each layer independently from the one above and the one below. The image on the right side shows two such layers: the "1" bits (dark spots) can easily be seen in each of the layers, as well as one "0" bit per layer. | |||
The ability to write on hundreds of different planes increases the amount of information that can be stored in a given volume of material (gigabits or terabits of data per cm<sup>3</sup> are achievable). | |||
<br clear='all'> | |||
=== Photochemistry Generated via an Intramolecular Electron Transfer === | === Photochemistry Generated via an Intramolecular Electron Transfer === | ||
[[Image:Tpa_photochemistry.png|thumb|300px|]] | [[Image:Tpa_photochemistry.png|thumb|300px|]] | ||
Another method to initiate this process with electron transfer. A two photon dye connected to a photoactive group will absorb the two photons | Another method to initiate this process is with electron transfer. A two-photon absorbing dye connected to a photoactive group will absorb the two photons and cause photoinduced electron transfer (PET) producing a radical anion and radical cation. This group can cleave to give rise to photoproducts. There is a history of doing this kind of chemistry not necessarily with dyes connected to each other and not with two-photon absorption. | ||
<br clear='all'> | <br clear='all'> | ||
=== | === 3D Micro- and Nano-fabrication === | ||
[[Image:Tpa_nanofab.png|thumb|300px| | [[Image:Tpa_nanofab.png|thumb|300px|SEM images of microstructures obtained by two-photon induced polymerization.]] | ||
There is a technology pull towards miniaturization of devices and patterned materials. | There is a technology pull towards miniaturization of devices and patterned materials. | ||
*Need to free-form | *Need to fabricate free-form structures in three dimensions with micron and sub-micron feature sizes | ||
*Increasing need | *Increasing need to pattern a variety of materials | ||
*Need to couple nano-scale object with micro-scale objects | *Need to couple nano-scale object with micro-scale objects | ||
*Areas impacted by 3D micro- and nano-fabrication include MEMs, microfluidics, photonics and tissue engineering. | *Areas impacted by 3D micro- and nano-fabrication include MEMs, microfluidics, photonics and tissue engineering. | ||
Two-photon induced polymerization (or other two-photon induced reaction) provides a means to fabricate three dimensional structures with a high degree of complexity and good fidelity, structures that can be difficult or time-consuming to make by other fabrication methods. A few examples of structures obtained by this fabrication technique in a polymer resin are shown in the figure: the photo on the left is a "chain link fence" that is twice the thickness of a human hair and has free-moving but interconnected parts. The second figure shows a series of channels; the third is a photonic crystal structure. The image on the right shows a series of criss-cross lines that could potentially be used as a scaffold for tissue engineering, as cells grow better on certain topologies. | |||
<br clear='all'> | |||
==== Sub-Diffraction Limited Resolution ==== | |||
[[Image:Tpa_subdiffraction.png|thumb|300px|TPA microfabrication of subdiffraction scale features. The lines are 170 nm wide.]] | |||
Current lithography techniques are able to make structures at 60 nm. However TPA microfabrication can produce features close to this size and with 3D resolution. In this example, the width of the lines is about 170 nm and they were obtained by two-photon induced polymerization with 730 nm laser light. | |||
<br clear='all'> | <br clear='all'> | ||
==== Negative Tone Resist ==== | |||
[[Image:Tpa_neg_tone.png|thumb|300px|Top: In a negative tone resist, exposed areas (yellow) remain after development. Bottom: example of a negative tone resist containing a two-photon initiator.]] | |||
This is an example of a TPA dye that creates a radical initiator after excitation. The radicals generated can then initiate polymerization in a resist (for example an acrylate). The polymer is less soluble than the starting resin and the nonpolymerized material can be removed by immersion in the solvent. Only the exposed areas that are attached to the substrate (or linked to each other) remain after development in the solvent. This is known as a negative tone resist. | |||
<br clear='all'> | |||
==== Positive Tone Resist ==== | |||
[[Image:Tpa_positivetone.png|thumb|300px|Top: In a positive tone resist the exposed areas (yellow) are removed (grey) during development. Bottom: example of a positive tone resist containing a two-photon photoacid generator.]] | |||
=== Micro-electromechanical Systems (MEMS) Applications === | A positive tone resist becomes more soluble in the areas that are exposed to light. This allows you to carve out parts of the material by exposure to light and then immersion in a suitable solvent. | ||
Micro electro mechanical systems are used for sensors, actuators, micromachines and optical switches. Inkjet heads and disc drive heads are MEMS. These can be fabricated with negative and positive tone materials. | |||
Tetrahydropyran can be protonated on the oxygen creating a carbocation thus converting the ester to a carboxylic acid. Esters are not soluble in basic water but acids are. So you can dissolve away selectively the converted material by dipping the sample in an alkaline solution; this is an example of a positive tone resist. A proton is needed to activate the conversion. | |||
A photoacid generator (PAG) is a compound that after absorption of light releases an acid. For example, in the structure shown, the excited compound can transfer an electron to the carbon-sulfur sigma orbital, causing the bond to break homolytically and yielding a methyl radical, which will attack the benzene and create a proton. The proton then starts the ester-to-acid reaction in the positive tone resist. The PAG shown here has a large TPA cross section and it has been used for two-photon induced microfabrication, as in the microchannel structure shown here. Notice that the two "pools" at the top of the structure are connected by a series of very fine tubes below the surface. | |||
[[Image:Tpa_microchannels.png|thumb|300px|Top: Schematic of microchannel structure. Bottom: Two-photon induced fluorescence images of the structure, fabricated in a positive tone resist, at various depths in the material (the central image is a cross section halfway along the channel lengths).]] | |||
<br clear='all'> | |||
==== Micro-electromechanical Systems (MEMS) Applications ==== | |||
Micro-electro mechanical systems are used for sensors, actuators, micromachines and optical switches. Inkjet heads and disc drive heads are MEMS. These can be fabricated with negative and positive tone materials. | |||
[http://www.memx.com/image_gallery.htm MEMS image gallery] | [http://www.memx.com/image_gallery.htm MEMS image gallery] | ||
=== 3D Microscopy Imaging === | |||
= | If a particular organelle or cell structure can be labeled with fluorescent TPA dye, by scanning a laser beam at the appropriate wavelength and recording the fluorescence emitted by the dye, it is possible to obtain a 3D mapping of the distribution of the dye with submicron resolution and thus a model of the structure to which the fluorescent dye is attached. Laser scanning fluorescence microscopy using TPA dyes is nowadays extensively used for imaging in biology or other area.<br clear='all'> | ||
A key factor in this technology is the availability of suitable labeling molecules that are affective two-photon absorbers (i.e. have large ''δ'' values) and are highly fluorescent. | |||
== Summary == | |||
== | Perturbation theory can been used to express the TPA cross section as a function of molecular parameters, such as state energies and transition dipole moments. This information and knowledge on how these parameters change with molecular structure have been used to predict which molecules have large TPA cross sections. One such class of compounds are linear conjugated molecules with a symmetric arrangement of electron donating or withdrawing groups, as these molecule have a large change in the quadrupolar charge distribution from the ground to the excited state and large coupling between the relevant excited states. | ||
<br clear='all'> | |||
For the measurement of TPA cross sections and the observation of TPA induced effects short pulses and large photon fluxes need to be used. Experiments need to be carried out with great care, to ensure that results are not affected by processes other than TPA, that sources of noise and error are minimized, and that the experimental conditions are consistent with the assumptions inherent in the models used to analyze the data. | |||
<br clear='all'> | |||
TPA can be exploited in many technological applications, including microfabrication, optical limiting, and 3D microscopy. | |||
==External Links== | |||
see [[wikipedia: Two-photon_absorption]] | |||
[[category:third order NLO]] | [[category:third order NLO]] | ||
Latest revision as of 12:05, 5 April 2011
| Previous Topic | Return to Third-order Processes, Materials & Characterization Menu | Next Topic |
Two-photon absorption (TPA) is a third order nonlinear optical phenomenon in which a molecule absorbs two photons at the same time. The transition energy for this process is equal to the sum of the energies of the two photons absorbed. The probability that a molecules undergoes two-photon absorption depends on the square of the intensity of the incident light, if the two photons are from the same beam (in the case of two incident beams, the transition probability depends on the product of the beams intensities). This intensity dependence is at the origin of the interest in two-photon absorbing materials for use in microscopy and microfabrication applications.
Two-Photon Excited Processes
Two-Photon Absorption
Two-photon absorption in a material can be quantified by the two-photon absorption cross section, a quantity that is proportional to the imaginary component of the χ(3) tensor (or, on a molecular level, to the imaginary component of γ) and depends on the photon energy/energies. In the following we will discuss in detail the case of degenerate (or one-color) two-photon absorption, that is the case where the two photons have the same energy. The figure at right schematically illustrates the degenerate two-photon absorption process, in which two photons, each of energy hνA, are simultaneously absorbed and the molecule is excited directly from the ground (S0) state to an excited state (state S2 in the figure) without the formation of an intermediate eigenstate. Neither of the two photons has enough energy to excite the molecule to S2 by itself, but the sum of the energies of the two corresponds to the energy of state S2. The dotted line represents a virtual state (as opposed to an actual eigenstate of the system) that can be thought of as created by the absorption of the first photon and having a very short lifetime (on the order of 10-15 sec if the photon energy is not in resonance with any electronic transition). If a second photon is absorbed within this lifetime, the two-photon absorption transition occurs and the molecule is excited to S2.
Once the molecule is in state S2, it quickly relaxes by internal conversion to the lowest excited state (S1 in the figure). From this state, the system can return to the ground state S0 by emission of fluorescence or by nonradiative decay. Alternatively, an additional photon can be absorbed (bringing the molecule to a higher-lying excited state, Sn), or electron or energy transfer to another molecule can take place. Typically, once the molecule is in state S1, the same set of processes will take place whether the molecule was initially excited into S2 by two-photon absorption or directly into S1 by one-photon absorption. For most known materials the two-photon absorption cross section, δ, is small and it is necessary to use intense laser beams in order to observe the effects of two-photon absorption.
The rate equation that describes the formation of the excited state of a molecule by one-photon absorption can we written as follows:
- <math>\frac {dN_{OP}} {dt} = \sigma N_{GS} F\,\!</math>
where
- <math>\sigma\,\!</math> is the one-photon absorption cross section (related to the transition dipole moment of the molecule between the initial and final states of the transition)
- <math>N_{GS}\,\!</math> is the number of molecules per unit volume in the ground state
- <math>N_{OP}\,\!</math> is the number of molecules per unit volume in the excited state due to one-photon absorption
- <math>F\,\!</math> is the photon flux (number of photons per unit area and time)
- <math>t\,\!</math> is the time
(this is analogous to the equation to describe the rate of a reaction between two reactants, A and B, to give a product C: A + B = C, and that is first-order with respect to each of the reactants).
In a similar manner, the rate equation for two-photon absorption can be written as follows, keeping in mind that two photons are needed to produce one excited molecule (in the reaction analogy, the reaction is now second-order in the photon flux, but still first-order in the concentration of molecules):
- <math>\frac {dN_{TP}} {dt} = \frac {1}{ 2} \delta N_{GS} F^2\,\!</math>
where
- <math>\delta\,\!</math> is the two-photon absorption cross section
- <math>N_{TP}\,\!</math> is the number of molecules per unit volume in the excited state due to two-photon absorption
This shows that the probability of two-photon absorption depends on the square of the photon flux (or, equivalently, to the square of the light intensity). The selection rules for the two-photon absorption process are different from those for one-photon absorption (in analogy to the situation for infrared and Raman spectroscopies). In particular, a two-photon absorption transition is allowed only between two states that have the same parity. Thus, in molecules with an inversion center, transitions are two-photon allowed from a gerade (g) state to another gerade state or from an underage (u) to another ungerade state, but not between g and u states. In the case of one-photon absorption, instead, transitions are allowed between an initial state and final state with opposite parity (from g to u, or vice versa). This implies that, in centrosymmetric molecules, if the transition from the ground state to a given excited state is one-photon allowed it is not two-photon allowed and, vice versa, if it is two-photon allowed it is not one-photon allowed. For molecules without inversion center, certain transitions can be both one-photon and two-photon allowed. In the scheme above, the blue arrow represents the excitation of a centrosymmetric molecule to the lowest excited state, S1, by the absorption of one photon (with one-photon absorption cross section σ); this transition is not two-photon allowed. The molecule can be excited by two-photon absorption (red arrows) into a higher-lying state, S2 (with two-photon absorption cross section δ).
Advantages of TPA
Two-photon absorption is considered to be a nuisance in the case of all-optical switching using χ(3) materials because it causes attenuation of the light beam and damage to the material can result from severe heating of samples. However the two-photon absorption process can be exploited in another contexts, apart from being of interest in the study of fundamental spectroscopic properties of materials.
Two-Photon Processes Provide 3-D Resolution

If a light beam is focused into sample at a wavelength suitable for one-photon absorption, molecules are excited throughout the beam path in the sample, as evidenced by the fluorescence emission in the bottom part of the cuvette at right. If the beam is tuned at a wavelength at which the material exhibits two-photon absorption, only the molecules located very close to the focus of the laser beam are excited (top beam in the photograph). This is related to the fact that the excitation rate depends on the square of the light intensity, as discussed above, and that in a focussed beam the light intensity is maximum at the focal plane and decreases approximately with the square of the distance from the focal plane, z, along the propagation direction (because the area of the beam increases moving away from the focus). Overall, the excitation rate for TPA and the intensity of the two-photon induced fluorescence decrease as the forth power of the distance from the focal plane. Consequently, in the solution in the figure the two-photon induced fluorescence is strongest at the beam focus and its intensity drops off very quickly on either side of the focal plane, resulting in what looks like emission from a "single point" (or small volume) in the solution. At the diffraction limit, the TPA excitation is confined to a volume on the order of the cube of the wavelength of the excitation light. Most of the applications of TPA are based on this ability to confine and control the excitation volume in a material with good resolution in three dimensions, as any excited state process that can take place in the material after two-photon excitation (such as fluorescence emission or energy transfer) will be confined to the same small volume.
TPA Processes Provide Improved Penetration of Light Into Absorbing Materials

In the figure at right the same two beams as in the case above are focused in a solution of a fluorescent compound, but now the solution is much more concentrated. It can be seen that for the bottom beam (one-photon absorption case) fluorescence emission can be seen only close to the right wall of the cuvette, as the beam is strongly absorbed and attenuated by the solution (the beam is propagating from right to left). Thus the penetration depth of the beam in the solution is small. In the case of the top beam, there is no one-photon absorption and two-photon absorption only occurs near the focus of the beam (in this case the center of the cuvette), so that there is no beam attenuation before the beam reaches the focus and the laser beam can penetrate farther into a sample with respect to the one-photon absorption situation. The ability to penetrate a material and to be focused accurately in three dimensions make the TPA process ideal for fluorescence imaging of thick samples (even in vivo) or in medical applications in which, for example, a drug can be activated by TPA at a very precise location without affecting the tissue above and below the focal plane of the excitation beam.
Measuring the Two-Photon Absorption Cross Section
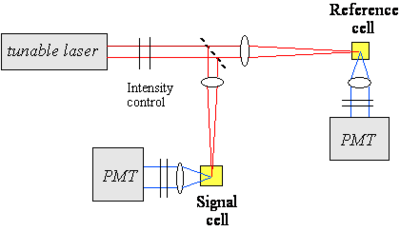
One of the techniques used to measure the TPA cross section of a material is based on two-photon induced fluorescence. In this measurement, a laser beam is propagated through the sample of interest (the beam can be focused or collimated) and the fluorescence light that is emitted by the excited molecules after two-photon absorption is collected and measured by a detector (for example a photomultiplier tube, PMT). As seen above, the number of molecules excited by two-photon absorption per unit time and volume, NTP, is proportional to the TPA cross section of the material at that excitation wavelength, the concentration of molecules and the square of the photon flux. The number of fluorescence photon emitted by these molecules is then:
- <math>n_{fl} = \eta N_{TP}\,\!</math>,
where η is the fluorescence quantum yield of the material.
Thus, the intensity of the two-photon induced fluorescence is proportional to the TPA cross section δ. This technique can be used for absolute or relative measurements of TPA cross sections. In the absolute case, all the relevant parameters (such as the instantaneous photon flux and the detection efficiency of the optical setup) need to be measured independently. In relative measurements, an unknown compound is analyzed under the same conditions as a material of known TPA cross section. The figure at right shows an example of optical setup that can be used for TPA cross section measurements. A tunable laser is needed to measure the TPA spectrum, as the TPA cross section depends on the excitation wavelength. In this example, the laser beam is split in two by a beam splitter and one of arm is used as reference for the intensity of the beam, to correct for fluctuations in intensity from pulse to pulse during the course of the measurement.
Measurement Considerations:
- A pulsed laser is needed (pulse durations in the ns, ps, fs range can be used).
- The laser need to be tunable to obtain spectral information on the material.
- The two-photon fluorescence method is applicable only to fluorescent materials (the z-scan technique can be used for fluorescent and non-fluorescent materials).
- The detection of the fluorescence emission can be done in various configurations (90º collection, backward scattering, forward scattering, ...); scattering of the excitation beam by the sample needs to be removed from the fluorescence signal before detection (for example using filters or monochromators).
- The dependence of the two-photon induced fluorescence signal on the square of the laser beam intensity needs to be tested for the actual experimental conditions used, to exclude contributions from other effects.
- Possible reasons for deviation from the dependence on the square of the laser intensity: linear absorption, stimulated emission, ground state depletion, ...
- Importance of spatial and temporal profile of the excitation beam.
See equipment video on Two-Photon Spectroscopy
Calculation of TPA Cross Sections
Perturbative Expression for γ, as Relevent to Two-Photon Absorption
The perturbative expression for the hyperpolarizability γ for the frequency component relevant to two-photon absorption can be written as follows (under the assumption that the system can be described by the so-called "three level model", in which only the ground state, g, the lowest excited state, e, and a higher-lying two-photon allowed state, e', are considered):
- <math>\gamma( -\omega; \omega, -\omega, \omega) \propto \frac{ M^2_{ge} \Delta \mu^2_{ge}} {(E_{ge} - \hbar \omega - i \Gamma_{ge})^2(E_{ge}-2\hbar \omega -i \Gamma_{ge})} + \frac {M^2_{ge} M^2_{ee^{\prime}}} {(E_{ge} - \hbar \omega- i \Gamma_{ge})^2 (E_{ge^{\prime}} - 2 \hbar \omega - i\Gamma_{ge^{\prime}})}\,\!</math>
where:
- <math>M_{ge} \,\!</math> is the transition dipole moment between states g and e
- <math>M_{ge^{\prime}} \,\!</math> is the transition dipole moment between states g and e'
- <math> \Delta \mu_{ge} \,\!</math> is the difference between the dipole moment of states g and e
- <math>E_{ge} \,\!</math> and <math>E_{ge^{\prime}} \,\!</math> are the energies for the transitions between the subscripted states
- <math> \omega \,\!</math> is the angular frequency of the excitation beam and
- <math> \Gamma \,\!</math> are damping terms.
For a centrosymmetric molecule <math>\Delta \mu_{ge}\,\!</math> goes to zero (the dipole moment is zero in both g and e states) so that the first term in the equation for γ goes to zero. For non centrosymmetric molecules both terms contribute to the hyperpolarizability. From the equation above it can be seen that two-photon resonances can occur when the photon energy is such that: <math> 2 \hbar \omega = E_{ge} \,\!</math> or <math> 2 \hbar \omega = E_{ge^{\prime}} \,\!</math>
The TPA cross section (δ) is proportional to the imaginary component of γ:
- <math>\delta(\omega) = \frac {4\pi^2 \hbar \omega^2} {n^2c^2} L^4 Im \gamma( -\omega; \omega, -\omega, \omega)\,\!</math>
The above equation is valid in the cgs system of units; <math> n\,\!</math> is the refractive index of the material, <math> L\,\!</math> is the local field factor (which depends on the refractive index), and <math> c\,\!</math> is the speed of light.
Calculations of the TPA Cross Section in a Donor-Acceptor Molecule
A simple donor/acceptor stilbene with an amino group and a formyl group on the phenyl rings in para position has been used a model compound for calculations of the TPA cross section. The figure at right shows the molecule in two resonance structures and the calculated TPA cross section as a function of the bond order alternation (BOA; i.e. the difference between the bond order in adjacent CC bonds in the vinylene bridge), which changes going from one resonance structure to the other. The value of δ for the transition from the ground to the first excited state (S0 to S1, left plot) is small for large negative values of the BOA (corresponding to the resonance structure on the left side), reaches a maximum when the BOA increases, and then it goes to zero when the BOA approaches the cyanine limit (BOA = 0). The same trend as a function of BOA is obtained for the change in dipole moments (see inset). The TPA cross section for the transition to the second excited state (S0 to S2, right plot) exhibits a more complicated behavior as a function of BOA and multiple peaks are present, in part because of changes in the detuning term <math>E_{ge} - \hbar \omega\,\!</math>. When the energy for the transition to S1 is very close to half of the energy for the transition to S2, the detuning term becomes small and δ increase; this situation is referred to a "double resonance".
See T. Kogej et.al. Chem. Phys. Lett. 1998, vol. 298, p. 1 [1]
Examples of Two-Photon Absorbing Materials
Two-Photon Absorption Spectrum of a Centrosymmetric Molecule
Here is a centrosymmetric molecule with a conjugated backbone and donor groups on both ends. The energy level diagram on the left side of the figure, similar to that discussed at the beginning of the section, shows the allowed transitions for this molecules. There can be one-photon excitation into S1 (this transition is not two-photon allowed because the molecule is centrosymmetric) and two-photon excitation into S2 (again for symmetry reason this transition is not one-photon allowed). After excitation, rapid relaxation can occur by internal conversion back to S1 and then fluorescence emission from S1. There is no fluorescence emission from S2 because, in most cases, the relaxation from S2 to S1 is much faster than the fluorescence lifetime. In centrosymmetric molecules this can be easily understood, because the transition from S2 to S0 is symmetry forbidden for one photon, therefore the transition dipole moment for this transition is close to zero and the coupling between the ground and the excited state is very small, resulting in a long radiative lifetime of the excited state. However even if the molecule was not centrosymmetric, the internal conversion relaxation from a higher-lying excited state is generally so fast that there still would not be fluorescence from S2 (or Sn). This is known as "Kasha's rule", which was described by Michael Kasha and which states that, irrespective of the electronic state of the molecule reached by excitation, fluorescence will only occur from the lowest lying excited state (S1). Most molecules behave according to Kasha's rule, but a few exceptions are known, such as azulene.
The figure also shows the one-photon (blue line) and two-photon absorption (red line) spectra of the molecule and the fluorescence emission spectrum (green line). In the graph note that the photon energy of the TPA band is lower (longer wavelength; the horizontal axis represent the wavelength of the excitation beam) than the one-photon absorption band (blue line) and of the fluorescence (green line). The TPA peak is around 720 nm, for this molecule. As two photons are involved in the transition, a TPA peak at 720 nm corresponds to a "transition wavelength" of 720 nm / 2 = 360 nm. The peak for linear absorption to S1 is 430 nm. This shows that the state reached by two-photon absorption is higher in energy than the S1 state and that there is very little one-photon absorption in this range (the small absorption seen at 360 nm is due to vibronic sub-levels of S1), consistent with the selection rules described earlier for centrosymmetric molecules.
see Rumi et al., J. Am. Chem. Soc. 2000, vol. 122, p. 9500 [2]
Laser Dyes
Xu and Webb measured the TPA cross section for various laser dyes and other commercially available compounds. The values at the peak of the two-photon absorption band for a selection of these compounds are reported at right. The TPA cross section is given here in goeppert-mayer (GM) units: 1 GM = 1 × 10-50 cm4 s molecules−1 photon−1. The unit is named in honor of Maria Goeppert Mayer, the German physicist that predicted the process of two-photon absorption in 1931. TPA was not actually observed experimentally until the early 60s, when lasers were developed that had sufficient intensity to lead to measurable effects in materials. One dye shown here has a cross section of about 300 GM, the other are in the range 10-100 GM.
See Xu and Webb, J. Opt. Soc. Am. 1996, vol. 13, p. 481; [3] Albota et al., Appl. Opt. 1998, vol. 37, p. 7352; [4] Fisher et al., Appl. Spectrosc. 1998, vol. 52, p. 536. [5]
Vagaries of TPA Measurements: The “famous” AF-50
The chart shows various measurements of the TPA cross section for the molecule AF-50. It can be seen that the values vary over many orders of magnitude. What is the reason for these differences? Is the problem intrinsic in the material or due to the way in which the parameter was measured? The measurements were indeed made using various techniques and conditions. The quantity δ is a molecular characteristic and it should not depend on the experimental conditions and optical set-up used. The variation in value in the chart is in part indicative of the measurement problems in the NLO field in general, as these are affected by relatively large uncertainties under the best of circumstances. In the case of TPA absorption, though, there can be additional problems, because some experimental techniques may not be selective to measure only TPA and for certain intensity ranges and pulse duration other effect may contribute to the observed signal. For example, the experiment that gave a δ value of 11560 GM was based on the nonlinear transmission (NLT) technique and conducted using pulses with duration of a few nanoseconds. It is now recognized that for pulse duration this long, many materials exhibit other nonlinear absorption processes in addition to TPA, in particular there can be excited state absorption (ESA) from S1 to a higher state Sn, if the population of S1 becomes large enough. During the NLT measurement the combined effect of TPA and ESA is seen and results in an apparent TPA cross section that is very large. This is, however, not the "intrinsic" cross section of the material, but an "effective" cross section that depends on the excitation conditions used in the experiment. While this is detrimental for the measurement of the "intrinsic" cross section, the large magnitude of the "effective" cross sections in some materials could be useful, for example, in making coatings for safety glasses that could exclude high intensity laser light (i.e. to achieve "optical limiting").
Initial Observations on a Bis-Donor Stilbene
A stilbene derivative (BDAS) with two π-donor groups (dibutyl amino group) is an instructive molecule to study.
Evidence for two-photon absorption
- Strong blue fluorescence was observed when pumped with orange laser light
- Fluorescence intensity for pumping with orange light depends on I2
- Strong nonlinear transmission was observed (that is the transmittance of the material changes as a function of the intensity of the excitation laser beam)
For this compound, the maximum TPA cross section (at 600 nm), δ was measured to be 210 x 10-50 cm4 s/photon, while for stilbene (i.e. if the two donor groups are removed) δ = 12 x 10-50 cm4 s/photon. Thus, the TPA cross section of BDAS is about 20 times that for the molecule without the electron donor groups. δ for BDAS is very large and it is useful to understand why the donors have this effect.
Interesting features for two-photon applications
- High fluorescence quantum yield, φfl ~ 0.9
- High optical transmission at low intensity
- Low oxidation potential, ED+/D = + 0.035 V vs. Fc/Fc+ (this compound is very easy to oxidize in the ground state and is a powerful reducing agent in the excited state)
Proposed Model to Enhance TPA Cross Sections in Symmetrical Molecules
Theoretical calculations can help to explain the properties of the BDAS molecule.
Calculations show that BDAS has large and symmetrical charge transfer from nitrogens (becoming more positive) to the vinyl group in the middle (becoming more negative) when the molecule is excited from S0 (g) to S1 (e) and to S2 (e') and this charge transfer is reflected primarily in very a large transition dipole moment between S1 and S2 (<math>M_{ee^{\prime}}\,\!</math>). The value of <math>M_{ee^{\prime}}\,\!</math> is much smaller in the case of stilbene.
These results suggest that a large change in quadrupole moment between S0 and S2 can lead to large values of δ.
Effect of Bis-Donor Substitution
The observation above suggests certain design strategies for increasing the dipole or quandrupole moment: if you want to make the dipole (or quadrapole) moment larger you can increase the distance over which charge is separated and you can increase the charge that is separated by that distance, or do both. The first would correspond to increasing the length of the molecule, the second to introducing functional groups that can facilitate the charge transfer. This is the role that the dibutylamino groups play in BDAS with respect to stilbene. This interpretation is supported by results of quantum chemical calculations performed on these molecules (in the calculations, dimethyl- instead of dibutyl-amino groups were considered). The transition dipole moment between the ground and first excited state is 7.2 D for stilbene and 8.9 D for BDAS. The biggest change, though, is observed for <math>M_{ee^{\prime}}\,\!</math>, as the transition dipole goes from 3.1 D in stilbene to 7.4 D for BDAS.
A simplified expression for the maximum TPA cross section for the transition to e' in centrosymmetric molecules can be obtained from the three-level equation given earlier for γ (keeping in mind that δ is proportional to Im γ):
- <math>\delta_{g \rightarrow e^{\prime}} \propto \frac {M^2_{ge} M^2_{ee^{\prime}}} {(E_{ge} - \hbar \omega )^2 \Gamma_{ge^{\prime}}} \,\!</math>
The term <math>M_{ee^{\prime}}\,\!</math> is squared in the equation and it can be seen that an increase in the value of this parameter from stilbene with respect to BDAS is the reason for the very high TPA cross section for BDAS.
Transition Dipole Moments
If the components that contribute to transition dipole moments are located farther from the middle of the molecule the contribution to the transition dipole moment is correspondingly larger. This is illustrated at right, where the change in charge distribution is plotted for the various atoms in the molecules. It can be seen that in BDAS one of the largest changes occurs on the nitrogens, which are located at the opposite ends of the molecule. This change, coupled with the extended distance from the molecular origin results in a large transition dipole moment for this molecule. In stilbene, the charge distribution changes mostly in the central part of the molecule, resulting in a smaller transition dipole moment <math>M_{ee^{\prime}}\,\!</math> .
There is an optimal amount of charge transfer that is needed to get the largest cross section.
Optical Limiting via Two-Photon Absorption in Bis-Donor Stilbene
It was mentioned above that nonlinear transmission was observed in BDAS. This material behaves as a good optical limiter for nanosecond pulses (see plot on the left side of the figure, for two different concentrations). This is due to the fact that the TPA cross section of this molecule is large, as seen above, and that this molecule also has a large excited state absorption cross section; when the molecule is excited with nanosecond pulses at a wavelength between 550 and 650 nm, a cascade of TPA and ESA processes takes place, resulting in large attenuation of the incident beam (optical limiting). The plot on the right side of the figure displays the TPA cross section of the compound obtained from a two-photon induced fluorescence measurement (ps-TPF, shown in red) and the nonlinear transmission spectrum (ns-NLT, shown in blue), that is the values of "effective" TPA cross section obtained from a NLT experiment with ns pulses: the two curves are similar in shape, but the scales of cross sections are different. The ns-NLT scale has units of 10-46 cm4 s/photon and the ps-TPF spectrum is on the scale of 10-48 cm4 s/photon, a factor of 100 difference. This is another example of the fact that NLT measurement performed with long pulse durations yield only the "effective" TPA cross section, which involves two-photon absorption followed by excited state absorption, as opposed to the "intrinsic" TPA cross section, which can be obtained from two-photon induced fluorescence measurements or other techniques that allow to exclude the effect of ESA (such as z-scan measurements with fs pulses at moderate peak intensities of the laser beam).
Design of TPA Chromophores
Three-Level Model and Transition Dipole Moments
We summarize here the expression for δ as a function of molecular parameters for a centrosymmetric molecule within the three-level model approximation and discuss how this can be used to derive guidelines for the design of chromophores with large TPA cross section:
- <math>\delta _{max} = f(\omega, n) \frac {M^2_{ge} M^2 _{ee^{\prime}}} {(E_{ge} - \hbar\omega)^2 \Gamma_{ge^\prime}}\,\!</math>
where:
- <math>\delta_{max}\,\!</math> is the cross sections at the peak of the TPA band (i.e. for <math>\hbar \omega\,\!</math> = <math> (1/2) E_{ge^{\prime}}\,\!</math>).
- <math>M_{\alpha\beta}\,\!</math> is the transition dipole moment for two levels α and β
- <math>E_{\alpha\beta}\,\!</math> is the energy difference between levels α and β
- <math>\hbar \omega\,\!</math> is the photon energy.
- <math>\Gamma_{ge^{\prime}}\,\!</math> is the damping term (typically on the order of 0.1 eV)
In summary:
- <math>\delta_{max} \propto M^2_{ge} M^2_{ee^\prime} \Delta E^{-2}\,\!</math>
where <math>\Delta E\,\!</math> is the detuning energy: <math>\Delta E\ = E_{ge} - \hbar \omega \,\!</math>
This suggests that to obtain large δ values, one of the following strategies can be used, at least in the case of centrosymmetric molecules, to increase the magnitude of one or both transition dipole moments:
- Increase the distance between the donors, so as to increase the distance over which the charge is transferred.
- Increase the strength of the donors, so as to increase the amount of charge that is transferred.
- Add acceptors to the middle of molecule, to further increase the amount of charge transfer.
- Flip the relative position of donors and acceptors in the molecule, using donors in the center and acceptors on the ends.
The diagram reports the TPA cross section (numbers under the molecular structures, in GM units) for a series of molecules with phenylene-vinylene conjugated backbones, to show the effect of donors (shown in blue) and acceptors (shown in red), as well as longer molecular chain lengths. The trend observed for δ in these compounds is consistent with the expectations based on the three-level model. The combination of these design strategies allows to achieve cross section on the order of thousands of GM. The trend in cross section when the molecular structure is changed are further illustrated in the following two sub-sections.
Chain-Length Dependence
The graph shows that as the length of the conjugated bridge increases, the energy of the two-photon absorption band decreases (the maximum in TPA band shifts to longer wavelength) and the magnitude of the TPA cross section increases, due to the increase of the transition dipole moment <math>M_{ge}\,\!</math>.
Effect of D/A Substitution
The table shows that by making these molecules quadrupolar, that is attaching electron-donating and/or electron-withdrawing functional groups on the conjugated backbone in a centrosymmetric arrangement, the TPA cross section increases significantly with respect to molecules without substituents. This is mainly due to the increase in the transition dipole moment <math>M_{ee^\prime}\,\!</math>: in fact this parameter is much larger in the molecule with donors at the termini of the molecule (second row in the table), than the one without donors (first row); the transition moment becomes even larger when the molecules contains both donor and acceptor groups (last three rows).
Applications for TPA
Two-Photon Initiated Polymerization and 3D Microfabrication
Two-photon absorption can be used to initiate photo-polymerization on a precise microscopic scale in 3D. A beam can be focused at a desired position in a polymer precursor, an initiator in the precursor is excited by two-photon absorption, photoactivating the polymerization or cross-linking in the material. This process is confined to the vicinity of the excitation volume. When the laser beam is moved to a different position, the polymerization or cross-linking is initiated in the new location. Then the non-crosslinked portions (those that have not been exposed to the laser beam) can be washed away by a solvent. This process can be used for microfabrication, that is the fabrication of a polymeric structure at the microscale with good control of the feature sizes in three dimensions, by scanning the laser beam in a prescribed pattern. This process has been used to fabricate structures in various types of resins and high degree of complexity. Selected example can be found in the following publications:
Wu et al., Proc. SPIE, 1992, vol. 1674, p. 776 [6]
Maruo et al., Opt. Lett., 1997, vol. 22, p. 132 [7]
Cumpston et al., Nature 1999, vol. 398, p. 51 [1]
Kawata et al., Nature 2001, vol. 412, p. 697 "Micro bull"
Two-Photon Initiators with Enhanced Sensitivity
Regular photo-initiators are not excellent two-photon absorbers. A femtosecond laser can supply a beam with very large power and thus it may be possible, in some cases, to use them as initiators under two-photon excitation conditions. However, at this laser power damage to the material could occur. At the same time, if the laser power is too low, the microscopic structure obtained by the photopolymerization may not have sufficient mechanical strength after removal of the unexposed resin, or the process may not be reliable enough. To achieve good reliability and fidelity in the microfabrication process it is desirable to utilize photoinitiators that are efficient and that have a wide dynamic range in writing power. For conventional initiators used under two-photon excitation conditions, the writing power range (that is the ratio between the power at which damage starts occurring and the minimum power that gives well-formed structures) is usually small, for example it is between 1 and 2.5 for the first three initiators in the table at right. Newly developed two-photon absorbing dyes expand this range, up to a value of 50 for the bottom two examples in the table. This increase results mainly from the fact that these dyes have a much larger TPA cross section than conventional initiators. This lets you write more accurately and faster because the beam does not have remain in the same place as long. The figures are SEM images of the same nominal structure fabricated: below the writing threshold, resulting in an incomplete structure after removal of the unexposed resin (top image), within the writing power range (middle image), and above the damage threshold of the material (bottom image).
Fluorescent and Refractive Bit Optical Data Storage
This two-photon induced polymerization technique can be used in optical data storage applications. For example the compound shown at right is non-fluorescent, but it becomes fluorescent when the pendant acrylate groups are incorporated in an acrylate polymer. When this compound is mixed with other acrylate monomers and exposed to laser light at an appropriate wavelength and intensity, TPA-induced polymerization takes place and the resulting polymer is fluorescent. The resin in the unexposed areas remains non-fluorescent. The image at the bottom left shows two rows of fluorescent bits, obtained by two-photon induced polymerization, on the dark background of the unexposed resin.
After laser exposure, the polymer also has higher density, due to cross-linking, than the unexposed portions of the resin. If the density goes up and the polarizability of the material stays the same, the susceptibility goes up and the refractive index goes up. Thus, it is also possible to "read" the bits based on the contrast in refractive index. Peter Rentzepis at the UC Urvine is using this method to create a 3D optical memory.
Because of the three-dimensional confinement of the excitation volume that is characteristic of the TPA process, it is possible to write and read sets of bits in multiple layers within the material, each layer independently from the one above and the one below. The image on the right side shows two such layers: the "1" bits (dark spots) can easily be seen in each of the layers, as well as one "0" bit per layer.
The ability to write on hundreds of different planes increases the amount of information that can be stored in a given volume of material (gigabits or terabits of data per cm3 are achievable).
Photochemistry Generated via an Intramolecular Electron Transfer
Another method to initiate this process is with electron transfer. A two-photon absorbing dye connected to a photoactive group will absorb the two photons and cause photoinduced electron transfer (PET) producing a radical anion and radical cation. This group can cleave to give rise to photoproducts. There is a history of doing this kind of chemistry not necessarily with dyes connected to each other and not with two-photon absorption.
3D Micro- and Nano-fabrication
There is a technology pull towards miniaturization of devices and patterned materials.
- Need to fabricate free-form structures in three dimensions with micron and sub-micron feature sizes
- Increasing need to pattern a variety of materials
- Need to couple nano-scale object with micro-scale objects
- Areas impacted by 3D micro- and nano-fabrication include MEMs, microfluidics, photonics and tissue engineering.
Two-photon induced polymerization (or other two-photon induced reaction) provides a means to fabricate three dimensional structures with a high degree of complexity and good fidelity, structures that can be difficult or time-consuming to make by other fabrication methods. A few examples of structures obtained by this fabrication technique in a polymer resin are shown in the figure: the photo on the left is a "chain link fence" that is twice the thickness of a human hair and has free-moving but interconnected parts. The second figure shows a series of channels; the third is a photonic crystal structure. The image on the right shows a series of criss-cross lines that could potentially be used as a scaffold for tissue engineering, as cells grow better on certain topologies.
Sub-Diffraction Limited Resolution
Current lithography techniques are able to make structures at 60 nm. However TPA microfabrication can produce features close to this size and with 3D resolution. In this example, the width of the lines is about 170 nm and they were obtained by two-photon induced polymerization with 730 nm laser light.
Negative Tone Resist
This is an example of a TPA dye that creates a radical initiator after excitation. The radicals generated can then initiate polymerization in a resist (for example an acrylate). The polymer is less soluble than the starting resin and the nonpolymerized material can be removed by immersion in the solvent. Only the exposed areas that are attached to the substrate (or linked to each other) remain after development in the solvent. This is known as a negative tone resist.
Positive Tone Resist
A positive tone resist becomes more soluble in the areas that are exposed to light. This allows you to carve out parts of the material by exposure to light and then immersion in a suitable solvent.
Tetrahydropyran can be protonated on the oxygen creating a carbocation thus converting the ester to a carboxylic acid. Esters are not soluble in basic water but acids are. So you can dissolve away selectively the converted material by dipping the sample in an alkaline solution; this is an example of a positive tone resist. A proton is needed to activate the conversion. A photoacid generator (PAG) is a compound that after absorption of light releases an acid. For example, in the structure shown, the excited compound can transfer an electron to the carbon-sulfur sigma orbital, causing the bond to break homolytically and yielding a methyl radical, which will attack the benzene and create a proton. The proton then starts the ester-to-acid reaction in the positive tone resist. The PAG shown here has a large TPA cross section and it has been used for two-photon induced microfabrication, as in the microchannel structure shown here. Notice that the two "pools" at the top of the structure are connected by a series of very fine tubes below the surface.
Micro-electromechanical Systems (MEMS) Applications
Micro-electro mechanical systems are used for sensors, actuators, micromachines and optical switches. Inkjet heads and disc drive heads are MEMS. These can be fabricated with negative and positive tone materials.
3D Microscopy Imaging
If a particular organelle or cell structure can be labeled with fluorescent TPA dye, by scanning a laser beam at the appropriate wavelength and recording the fluorescence emitted by the dye, it is possible to obtain a 3D mapping of the distribution of the dye with submicron resolution and thus a model of the structure to which the fluorescent dye is attached. Laser scanning fluorescence microscopy using TPA dyes is nowadays extensively used for imaging in biology or other area.
A key factor in this technology is the availability of suitable labeling molecules that are affective two-photon absorbers (i.e. have large δ values) and are highly fluorescent.
Summary
Perturbation theory can been used to express the TPA cross section as a function of molecular parameters, such as state energies and transition dipole moments. This information and knowledge on how these parameters change with molecular structure have been used to predict which molecules have large TPA cross sections. One such class of compounds are linear conjugated molecules with a symmetric arrangement of electron donating or withdrawing groups, as these molecule have a large change in the quadrupolar charge distribution from the ground to the excited state and large coupling between the relevant excited states.
For the measurement of TPA cross sections and the observation of TPA induced effects short pulses and large photon fluxes need to be used. Experiments need to be carried out with great care, to ensure that results are not affected by processes other than TPA, that sources of noise and error are minimized, and that the experimental conditions are consistent with the assumptions inherent in the models used to analyze the data.
TPA can be exploited in many technological applications, including microfabrication, optical limiting, and 3D microscopy.
External Links
see wikipedia: Two-photon_absorption
- ↑ T. Kogej et.al. Chem. Phys. Lett. 1998, 298, 1.
- ↑ Rumi et al., JACS 122, 9500, 2000
- ↑ C. Xu, JOSA B, 1996;
- ↑ M. Albota, Appl. Opt., 1998;
- ↑ W. G. Fisher, Appl. Spectr., 1998.
- ↑ E. S. Wu, J. H. Strickler, W. R. Harrell & W. W. Webb, SPIE Proc. 1674, 776 (1992)
- ↑ S. Maruo, O. Nakamura & S. Kawata, Opt. Lett. 22, 132 (1997)