Difference between revisions of "Hyper Rayleigh Scattering"

From CleanEnergyWIKI
Jump to navigation Jump to search
m
 
(25 intermediate revisions by the same user not shown)
Line 1: Line 1:
Hyper Rayleigh Scattering (aka Harmonic Light Scattering or HRS) is one method for measuring the [[first hyperpolarizability]]β. Another method is electric field induced second harmonic generation (EFISH)
<table id="toc" style="width: 100%">
<tr>
<td style="text-align: center; width: 33%">[[Main_Page#Research Equipment, Devices and Techniques|Return to Research Tool Menu]]</td>
 
</tr>
</table>
Hyper Rayleigh Scattering (aka Harmonic Light Scattering or HRS) is one method for measuring the [[first hyperpolarizability]] &beta;.


=== Overview ===
=== Overview ===
Line 7: Line 13:
In HRS A dilute sample of a test chromophore is prepared in a solvent.  An incident laser generates a second harmonic signal, specifically the frequency double signal from excitation of the sample molecules.  This can be related to the beta of the sample using this formula:
In HRS A dilute sample of a test chromophore is prepared in a solvent.  An incident laser generates a second harmonic signal, specifically the frequency double signal from excitation of the sample molecules.  This can be related to the beta of the sample using this formula:


:<math>\frac {I_{sample}} {I_{solvent}} = \frac {N_{sample} \langle \beta^2 _{sample} \rangle  + N_{solvent} \langle \beta^2_{solvent}\rangle}   {N_{solvent} \langle \beta^2_{solvent}\rangle}\,\!</math>
:<math>I^ {2 \omega }_{HRS} = [ (I ^ \omega_0 \cdot T ^ \omega_{solv})^2 G ] ( N_{solv} \langle \beta ^ 2 _{solv} \rangle  + N_{sam} \langle \beta ^ 2 _{sam} \rangle ) \,\!</math>
 
where
:<math>I ^ \omega_0\,\!</math>  is the intensity of the incident field
:<math>T ^ \omega_{solv}\,\!</math> is the transmission of the fundamental radiation for the solvent
:<math>G\,\!</math> is the instrumental efficiency
:<math>N\,\!</math> is the number density of the sample (sam)and solvent (solv)
:<math>\beta^2\,\!</math> is the orientational average of the square of the first hyperpolarizability.


[[Image:Tcp1_chcl3.png|thumb|300px|HRS spectrum for 1.5 &mu;m TCP1 in CHCl<sub>3</sub>]]


See Firestone 2004 <ref>K. A. Firestone, P. Reid, R. Lawson, S. H. Jang, and L. R. Dalton, “Advances in Organic Electro-Optic Materials and Processing,” Inorg. Chem. Acta, 357, 3957-66 (2004)</ref>.
See Clays 1992 <ref>Clays, K.; Persoons, A., Hyper-Rayleigh scattering in solution. Rev. Sci. Instrum. 1992, 63 (6), 3285-9.</ref>.  
and Goovaerts 2001 <ref>Goovaerts, E.; Wenseleers, W. E.; Garcia, M. H.; Cross, G. H., Design and characterization of organic and organometallic molecules for second order nonlinear optics. Handbook of Advanced Electronic and Photonic Materials and Devices 2001, 9, 127-191</ref>


There are a number of ways the HRS setupcharacterization is used in non-linear optics research.
There are a number of ways the HRS characterization method is used in non-linear optics research.


The dielectric properties of the solvent influence the &beta; (solvatochromatism). One area of research involves predicting and solvent effects so as to better understand the performance of molecules when densely packed in materials. Attempts have been made to calibrate HRS measurements with EFISH measurements of beta though they are based on different tensor elements.
The dielectric properties of the solvent influence the &beta; (solvatochromatism). One area of research involves predicting and solvent effects so as to better understand the performance of molecules when densely packed in materials. Attempts have been made to calibrate HRS measurements with [[Electric-field induced second-harmonic generation | EFISH]] measurements of beta though they are based on different tensor elements.


See Wikipedia on [http://en.wikipedia.org/wiki/Rayleigh_scattering Rayleigh Scattering]
See Wikipedia on [http://en.wikipedia.org/wiki/Rayleigh_scattering Rayleigh Scattering]
Line 23: Line 36:
See Wikipedia on [http://en.wikipedia.org/wiki/Raman_scattering Raman Scattering]
See Wikipedia on [http://en.wikipedia.org/wiki/Raman_scattering Raman Scattering]
<br clear='all'>
<br clear='all'>
=== Technique ===
=== Technique ===
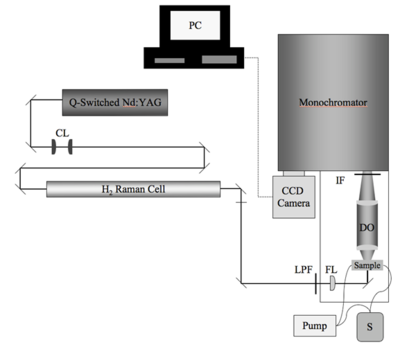
The HRS measurement of &beta; is a specialized device custom-built on an optics table. The components and configuration can change significant from site to site. It is important to understand the significance of each portion of the setup. One possible HRS experimental setup is described here.
The HRS measurement of &beta; is a specialized device custom-built on an optics table. A series of mirrors, filters and devices [[hydrogen raman cell]] pass a specific wavelength of light into a sample which then emits light that is selected by a  [[monochromator]] and then detected with a photocell. The components and configuration can change significantly from site to site. It is important to understand the significance of each portion of the setup. One possible HRS experimental setup is described here. (Press > to Play the video)
 
<swf width="550" height="430">http://depts.washington.edu/cmditr/media/rayleigh.swf</swf>


#Q-switched Nd:YAG laser operating at 1064 nm with a repetition rate of 30 Hz is directed along a double-back path in order to make it easier to adjust the optics along the path.
YouTube version:
#The beam is directed into a 1-m H2 Raman cell which produces 1907 nm (the first stokes line - near infrared) radiation. The desired wavelength is isolated Pellin-Broca prism, dichroic mirrors, and a Corning long-pass emission filter resulting in an incident power of 400mW.
{{#ev:youtube|IP1HH6giIZU}}
#The exciting beam is directed into a 10mm flow cell through which fresh sample is continually pumped so as to avoid the effects of photo degradation of the sample.
#Light scattered at 90 degrees from the excitation beam path is focused into a monochromatic containing a 1200 g/mm ruled diffraction grating and 950nm interference filter. This isolates radiation emitted at the second harmonic (2 omega) of the excitatory beam ( lambda/2= 1907 /2=950)
#Finally the specific desired wavelength was measured with a CCD camera with long exposures of 240-540 seconds.
#The HRS spectra is processed to remove low intensity background two-photon fluorescence which can be fitted to a fourth order polynomial and then subtracted.
#The final HRS spectra is fitted to a Gaussian functional form.
#At this point a number of mathematical manipulations and comparisons can be done, for example comparing the sample HRS to a known reference sample with known beta, or internal referencing of the solvent contribution of beta.


Low intensity background due to two-photon excited fluorescence can be fitted to a fourth order polynomial and subtracted.


Video to come
At this point a number of mathematical manipulations and comparisons can be done, for example comparing the sample HRS to a known reference sample with known beta, or internal referencing of the solvent contribution of beta.


=== Significance ===
=== Significance ===
Line 44: Line 55:


<br clear='all'>
<br clear='all'>
[[category:Research equipment]]

Latest revision as of 09:22, 28 June 2010

Return to Research Tool Menu

Hyper Rayleigh Scattering (aka Harmonic Light Scattering or HRS) is one method for measuring the first hyperpolarizability β.

Overview

Schematic of the HRS setup. CL = collimating lenses; LPF = long-pass filter; FL = 300-mm focusing lens; S = solution of chromophore in solvent of choice; DO = detection optics; IF = interference filter (950 nm)

In HRS A dilute sample of a test chromophore is prepared in a solvent. An incident laser generates a second harmonic signal, specifically the frequency double signal from excitation of the sample molecules. This can be related to the beta of the sample using this formula:

<math>I^ {2 \omega }_{HRS} = [ (I ^ \omega_0 \cdot T ^ \omega_{solv})^2 G ] ( N_{solv} \langle \beta ^ 2 _{solv} \rangle + N_{sam} \langle \beta ^ 2 _{sam} \rangle ) \,\!</math>

where

<math>I ^ \omega_0\,\!</math> is the intensity of the incident field
<math>T ^ \omega_{solv}\,\!</math> is the transmission of the fundamental radiation for the solvent
<math>G\,\!</math> is the instrumental efficiency
<math>N\,\!</math> is the number density of the sample (sam)and solvent (solv)
<math>\beta^2\,\!</math> is the orientational average of the square of the first hyperpolarizability.


See Clays 1992 [1]. and Goovaerts 2001 [2]

There are a number of ways the HRS characterization method is used in non-linear optics research.

The dielectric properties of the solvent influence the β (solvatochromatism). One area of research involves predicting and solvent effects so as to better understand the performance of molecules when densely packed in materials. Attempts have been made to calibrate HRS measurements with EFISH measurements of beta though they are based on different tensor elements.

See Wikipedia on Rayleigh Scattering

See also Density Functional Theory

See Wikipedia on Raman Scattering

Technique

The HRS measurement of β is a specialized device custom-built on an optics table. A series of mirrors, filters and devices hydrogen raman cell pass a specific wavelength of light into a sample which then emits light that is selected by a monochromator and then detected with a photocell. The components and configuration can change significantly from site to site. It is important to understand the significance of each portion of the setup. One possible HRS experimental setup is described here. (Press > to Play the video)

<swf width="550" height="430">http://depts.washington.edu/cmditr/media/rayleigh.swf</swf>

YouTube version:

Low intensity background due to two-photon excited fluorescence can be fitted to a fourth order polynomial and subtracted.

At this point a number of mathematical manipulations and comparisons can be done, for example comparing the sample HRS to a known reference sample with known beta, or internal referencing of the solvent contribution of beta.

Significance


References

  1. ↑ Clays, K.; Persoons, A., Hyper-Rayleigh scattering in solution. Rev. Sci. Instrum. 1992, 63 (6), 3285-9.
  2. ↑ Goovaerts, E.; Wenseleers, W. E.; Garcia, M. H.; Cross, G. H., Design and characterization of organic and organometallic molecules for second order nonlinear optics. Handbook of Advanced Electronic and Photonic Materials and Devices 2001, 9, 127-191


Retrieved from "http://cleanenergywiki.org/index.php?title=Hyper_Rayleigh_Scattering&oldid=7222"