Difference between revisions of "Electron-Phonon Coupling"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| Line 57: | Line 57: | ||
=== Charge Transport === | === Charge Transport === | ||
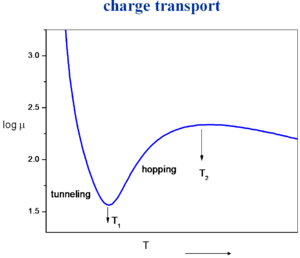
[[Image:chargetransport.png|thumb|300px|]] | [[Image:chargetransport.png|thumb|300px|Variation in charge mobility with temperature]] | ||
Currently we can not predict the crystal structure of a molecule given the chemical formula of a molecule. The big challenge is to evaluate the mobility as a function temperature. If you start with a perfect crystal at low temperature you have a large mobility. As the temperature increases the molecules start vibrating and there is a reduction in electronic coupling, bandwidth and mobility. In metals as you increase temperature the vibrations get larger and mobility comes down. At some point the vibrations will reduce the electronic coupling so much that it will become favorable for the charge carrier to localize. This cross over region is difficult to describe and may not be an abrupt evolution. There is a gradual localization process. Once you cross over into the hopping regime (an activated regime) with localization the mobility goes back up with temperature. Here the vibrations help by preparing the two molecules to achieve essentially the same geometry so that electron transfer can take place. So the rate of electron transfer is simply the time it takes for vibrations to bring the molecules into the same geometry. In most organic materials will have decomposed before they reach a temperature where they begin to decrease in electron transfer with temperature (T<sub>2</sub>). | Currently we can not predict the crystal structure of a molecule given the chemical formula of a molecule. The big challenge is to evaluate the mobility as a function temperature. If you start with a perfect crystal at low temperature you have a large mobility. As the temperature increases the molecules start vibrating and there is a reduction in electronic coupling, bandwidth and mobility. In metals as you increase temperature the vibrations get larger and mobility comes down. At some point the vibrations will reduce the electronic coupling so much that it will become favorable for the charge carrier to localize. This cross over region is difficult to describe and may not be an abrupt evolution. There is a gradual localization process. Once you cross over into the hopping regime (an activated regime) with localization the mobility goes back up with temperature. Here the vibrations help by preparing the two molecules to achieve essentially the same geometry so that electron transfer can take place. So the rate of electron transfer is simply the time it takes for vibrations to bring the molecules into the same geometry. In most organic materials will have decomposed before they reach a temperature where they begin to decrease in electron transfer with temperature (T<sub>2</sub>). | ||
Revision as of 15:22, 22 June 2009
| Previous Topic | Return to Transport Properties Menu |
A complete treatment of electron-phonon coupling
The frontier of research in organic semiconductors is attempting to get a complete picture of electron transport by understanding intramolecular and intermolecular vibrations. Several people have been working on this for a while. Silbey & Munn Bobbert et al. Troisi et al. Stafström et al. Shuai et al.
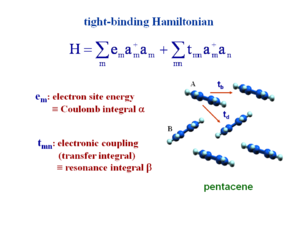
Tight-binding Hamiltonian
This is the second quantization form of the Hamiltonian. In Hückel calculations you describe a molecule as having an energy coulomb integral alpha. This is the energy of a site. To do a Hückel calculation for a polyene molecule you place an alpha on each carbon. The value of the alpha is the value of the pi atomic orbital for an isolated sp2 carbon.
The transfer integral (tmn) or electron coupling for adjacent molecules is the resonance integral beta in Hückel terminology. For example if you treat butadiene at the Hückel level there would be 4 carbons, each with a site energy alpha, and between carbons the resonance integral beta, which can be different for double B1 (shorter bonds have larger electronic coupling) and single bonds B2. The same could be done for the pentacene system. In the case of pentacene the two molecules of the units cells have slightly different surroundings and therefore the energies would slightly different. There would be beta1 and beta2 (for the tb and td directions). In the Hamiltonian alpha and beta become e and t. This gives you very compact way of writing an equation.
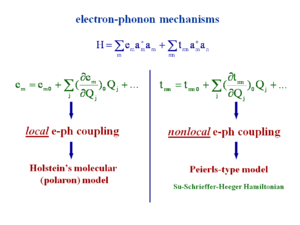
Electron phonon mechanism
Intramolecular and intramolecular modes of vibration are able to modify e an t. To get a complete description of the system you can look at the variation of the site energy as a function each the vibrational modes that are in the system. This equation looks at the site energy on molecule m and zero denotes the absence of vibration and then look at the impact of each of the vibrational modes (j) on the site. This shows the variation of site energy as you take into account vibrational modes. Some modes will have no impact, some will be significant. As you go to an ionized state there will be a strong geometry relaxation so there will be a strong coupling to the vibrational modes that lead to the ionized state.
The effect of temperature can be explained because the increased temperature causes excited levels of vibration with larger displacement, and large perturbation of the site energies. The same can be done for the transfer integrals. When you displace molecules from a perfectly cofacial orientation there were major variations in the electronic coupling. So this will have a large impact the transfer integral.
Considering the impact of vibrations on the site energy that is referred to as the “local” electron-phonon coupling. If you look at the impact on the transfer integral that is called the “nonlocal” electron-phonon coupling. In the last 40 years there have theories that take into account one or the other of these couplings, such as Holstein’s molecular polar model (local only), and the Peierls type model (nonlocal only), or Su-Schrieffer-Heeger Hamiltonian. These are all simple Hueckle theory varying beta depends on the bond length, and electronic coupling depends on bond C-C bond stretching. Beta or t vary depending on the mode.
Local electron-phonon coupling
Local electron-phonon coupling is the impact of vibrations from molecular relaxations (intra-molecular modes) on site energy there will be an impact from the polarization (intramolecular modes) as well librations (translations and rotations of molecule as whole) and in intermolecular modes.
The local electron-phonon coupling can be very significant due to intramolecular geometry relaxations
The polarization contributions still need more systematic investigations
Nonlocal electron-phonon coupling
Non local electron-phonon coupling is mostly a functon of intermolecular modes. Nonlocal electron-phonon coupling is large. This does not depend very much on the intermolecular geometry. Use the Condon approximation which says whatever geometry you used for the intramolecular electron coupling will be pretty much the same for the intermolecular geometry.
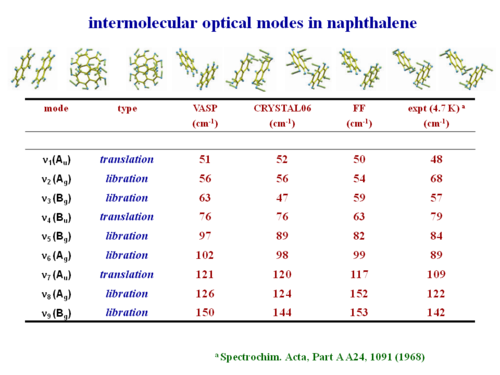
This shows the intermolecular optical modes in naphthalene. These can be evaluated and they have good agreement with experimental observation.
Currently we can not predict the crystal structure given the chemical formula of a molecule. Given a molecule the big challenge is to evaluate the mobility as a function temperature.
Charge Transport
Currently we can not predict the crystal structure of a molecule given the chemical formula of a molecule. The big challenge is to evaluate the mobility as a function temperature. If you start with a perfect crystal at low temperature you have a large mobility. As the temperature increases the molecules start vibrating and there is a reduction in electronic coupling, bandwidth and mobility. In metals as you increase temperature the vibrations get larger and mobility comes down. At some point the vibrations will reduce the electronic coupling so much that it will become favorable for the charge carrier to localize. This cross over region is difficult to describe and may not be an abrupt evolution. There is a gradual localization process. Once you cross over into the hopping regime (an activated regime) with localization the mobility goes back up with temperature. Here the vibrations help by preparing the two molecules to achieve essentially the same geometry so that electron transfer can take place. So the rate of electron transfer is simply the time it takes for vibrations to bring the molecules into the same geometry. In most organic materials will have decomposed before they reach a temperature where they begin to decrease in electron transfer with temperature (T2).
| Previous Topic | Return to Transport Properties Menu |