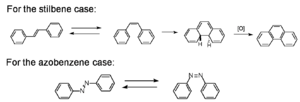Photochromism

Previous Topic

Return to Absorption and Emission Menu

Next Topic

Definition

Photochromism is a reversible transformation of a chemical species induced in one or both directions by absorption of electromagnetic radiation between two forms, A and B, having different absorption spectra. A common example is the sunglasses that turn dark when exposed to sunlight. In order to qualify as photochromic the different forms of the species must have different absorption spectra.

Good References Photochromism by Brown

Photochromism, Molecules, and Systems by Dürr

Photochromism is derived from the Greek words: phos (light) and chroma (color). When light of wavelength lambda1 is exposed to species A it goes to B and when B is exposed to light with wavelength lambda 2 or in the presence of heat, B goes to A.

<math>A \Leftrightarrow^{\lambda_1}_{\lambda_2, \Delta}B\,\!</math>

Species A gives rise to species B with a different absorption spectrum.

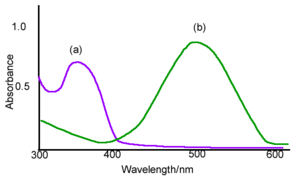
The example spectra of A absorbs around 350 nm and B absorbs around 500nm. One of the ways that you can control the transition is by changing the wavelength of the absorbing light, if they have different spectra. Photochromic materials are used in optical memory in which case you want A to go B and stay there. In this case it desirable that the heat driven transition from B back to A be very small.

The first report of photochromism was given by Fritzsche 1867 who observed the bleaching of an orange-colored solution of tetracene in the daylight and the regeneration of the color in the dark.

Tetracene is a four ring conjugated colored molecule. When the crystals are exposed to sunlight the molecule is broken into the two smaller molecules neither of which absorbs in the visible also known as bleaching. There is transient bleaching, permanent or semi transient types of bleaching.

Interconversion of Isomers

A photochromic conversion of A to B, and B to A can be described by the equations:

<math>

N_{A\rightarrow B} = N_A .f(\epsilon^A(\lambda), I(\lambda)). \phi_{A \rightarrow B}\,\!</math>

<math>N_{B\rightarrow A} = N_A .f(\epsilon^B(\lambda), I(\lambda)). \phi_{B \rightarrow A}+ N_B .f’(T)\,\!</math>

Where:

<math>f(\epsilon^X(\lambda), I(\lambda))\,\!</math> is the fraction of molecules of the species x that is excited by the light per unit time,

<math>f(\epsilon^X(\lambda), I(\lambda))\,\!</math> is a function of the extinction coefficient of the molecule :<math>[\epsilon^X(\lambda)]\,\!</math> at wavelength l and of the light intensity :<math>[I(\lambda)]\,\!</math> at that wavelength (the absorption spectra)

<math>\phi_{A\rightarrow B}\,\!</math> is the quantum yield the conversion of A to B

<math>\phi_{B\rightarrow A}\,\!</math> is the quantum yield of the conversion of B to A

<math>f'(T)\,\!</math> is the fraction of molecules B that thermally convert to A per unit time, it is a function of temperature [T] (thermal reversal)

The rate of absorption is the rate that molecules go from the ground to the excited state because of the collision with a photon. The rate law for this chemical reaction would be dependent on the concentration of A and the rate of photo flux and the probability of a photo being absorbed. In order for A to go to B it must achieve an excited state. The quantum yield predicts how often the excited state will lead to the formation of B as opposed to decaying, giving off a photo or other non-productive outcomes.

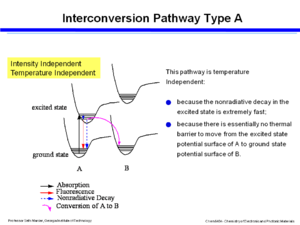
Interconversion – poor coupling

Consider the exited state and ground state potential surfaces. If you assume that the excited state potential well between A and B are not strongly coupled or do not interact then the photon is absorbed into the excited state, over a period of 100s of femptoseconds the molecule relaxes down to the lower vibrational levels within the excited state, and then it can go back down buy fluoresence or non-radiative decay. If the excited state of A goes directly to the ground state of B that will be a temperature independent process because it is extremely fast and because the excited state can slide easily back to the ground state of A because there is no thermal barrier. This pathway is intensity dependent.

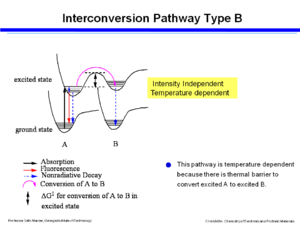
Interconversion- strong coupling

If there is strong coupling of the two potential wells in the excited state of the two species then energy moves by a thermally activated process in the excited states. You are not forming the ground state of B directly, instead you are forming an excited state of B which then goes to the ground state by fluorescence or non-radiative decay. This pathway is temperature dependent because there is thermal barrier to convert excited A to excited B. You can control the outcome of reaction and its equilibrium by changing the temperature. However it is not dependent on intensity.

Photostationary State

A photostationary state occurs when under irradiation the rate of A &rarr B equals the rate of B → A at dynamic equilibrium. This is dynamic because we are not a thermal equilibrium, we are continually adding photons. The details of the photons makes a big difference. Suppose you have a molecule A that absorbs at exactly 400nm and its counterpart B absorbs at 500nm. If you excite this molecule at 400nm and there is some quantum yield of A going to B and there little thermal conversion from B to A then the photostationary state will be 100% B. You are exciting A it goes to B but it has no way of getting back. If you excite at 500nm the the photostationary state will be 100% A. The distinction between the equilibrium and the photostationary state is that the latter depends on the wavelength of the light source, the overlap with the absorption spectra of the two molecules and the quantum yields for each of the reactions. It is the number of number of A or B over the total number of molecules.

The photostationary composition is defined as:

<math> N_{AorB}/(N_A+N_B)\,\!</math> at dynamic equilibrium

Here

<math>N_{A\rightarrow B}\,\!</math>= :<math>N_{B\rightarrow A}\,\!</math>

Thus:

<math>N_A .f(\epsilon^A(l), I(\lambda)). \phi_{A\rightarrow B} = NB .f(\epsilon^B(\lambda), I(\lambda)). \phi_{B\rightarrow A}+ NB .f’(T)\,\!</math>

The rate is determined by number of molecules, the overlap of extinction coefficient and the intensity of the light at each wavelength and the quantum yield. Light sources rarely have equal intensities over all wavelengths. When the two parts of the equation are equal there is photostationary state.

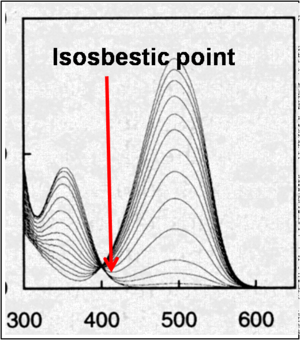
Isosbestic Point

Consider the absorption spectra of a composite comprised of A and B. The absorption at λ equals the number of molecules of A times the extinction coefficient of A at λ plus the number of molecules of B plus the extinction coefficient of B at λ.

At any wavelength the absorption at a given wavelength, A(λ), of a two-component system (photochromism is a special case) is given by:

<math>A(\lambda)= N_A \epsilon_A^{\lambda} + N_B\epsilon_B^{\lambda}\,\!</math>

If at one wavelength the extinction coefficients are equal they can be factored out:

<math>\epsilon_{A}^{\lambda} = \epsilon_{B}^{\lambda}\,\!</math>

That wavelength defines the isosbestic point because:

<math>A(\lambda)= \epsilon^{\lambda} (N_A + N_B)= \epsilon^{\lambda} N_{tot}\,\!</math>

The isobestic point is the point where the absorption remains constant. Thus at the isosbestic point the absorption is independent of the relative concentration of the two forms. Chemists often use this property to follow reactions that are not necessarily photochromic reactions. Assume that A goes to B but in order to get there it had to form C.

<math>A \Leftrightarrow C \Leftrightarrow B\,\!</math>

If C has a different absorption spectra than A or B the absorption spectra then all the curves would not cross at a single point. So when you run absorption curves and observe an isosbestic point that means there are no intermediates going from A to B that exist for an appreciable time. A very rapid formation and breakdown of C will not change the absorption spectra. If there is an isosbestic point either there are no intermediates, ie it’s a very clean reaction, or the intermediates have a very short lifetime.

Photochemical Reaction Fatigue

Photochemical fatigue has for many years limited the use of photochromic materials for optical memory. Even today rewriteable discs do not use photochromic materials, instead they utilize phase change going from one crystalline form to another that results in different reflectivity. A magnetic memory is written over hundreds of thousand of times, this is the requirement. For a photochemical to be useful it must have a very low quantum yield for any decomposition pathway. The quantum yield is independent of light intensity.

Recall that quantum yield for a process X is given by:

<math>\phi_x \,\!</math> = # of molecules that undergo process X/# of photons absorbed

or

<math>= k_x/ \sum k\,\!</math> for all processes leading to loss of excited-state population.

For photochromic reaction some important rates constants to consider are:

<math>k_{I\rightarrow>II}\,\!</math> rate of photochromic transformation

<math>k_r\,\!</math> rate of radiative decay (fluorescence)

<math>k_{nr}\,\!</math> rate of nonradiative decay

<math>k_{bl}\,\!</math> rate of photobleaching

Example Photochromic Reaction

An example of a photochromic reaction involving a spiropyran which is a merocyanin. This is a conjugated molecule. On the B form the O- is donor and the C double bond N+ is an acceptor. This leads to a charge transfer absorption band that makes the molecule purple. Whereas the A form has a benzene ring with a nitrogen that absorbs in the UV. The oxygen transfers charge to the nitrogen and this probably makes the molecule somewhat yellow. Ideally you want the quantum yield for phi 1 (A going to B) equal to the quantum yield for phi 2 (B going to A) and equal to 1. Thus every time you put in photon in it goes back and forth, and you control which way it goes by the wavelength of the photon.

Ideally Φ₁ = Φ₂ = 1, and Φ₃ = 0

Where Φ₁ is the quantum yield for the forward reaction

Φ₂ is the quantum yield for the reverse reaction and

Φ₃ is the decomposition quantum yield

Photochemical Degradation

However, if the quantum yield for degradation (i.e., formation of C) is f3, the non-degraded fraction y after n cycles will be:

<math>y = (1 - \phi_3)^n\,\!</math>

For very small f3, and when n is very large, the expression can be approximated as:

<math>y = (1 -n\phi_3)\,\!</math>

Thus, for even a highly reversible reaction with f3 = 0.001 (yield = 99.9%), after 1,000 cycles, 63% of A will be lost, and after 10,000 cycles effectively all of A will be destroyed. In synthetic chemistry a 90% yield is considered very good, here we are talking about a 99.9% yield. Thus you need a reaction with decomposition quantum yield of 10-5 or 10-6 to be useful for optical memory.

Cis- Trans Isomerizations

Stilbene and Azobenzene

There has been a lot of work molecules that use pericyclic and isomerization reactions to optimize them so they can be fully reversible. One reaction that was looked at early on was the cis-trans isomerization of stilbene. Common in stilbenes, azo compounds, azines, thioindigoids, etc., as well as some photochromic biological receptors that are part of living systems. These molecules have different absorption spectra. They can have different groups added causing the molecules to twist. If a benzene ring on stilbene were to twist 90 degrees it would no longer participate in the pi conjugation. The benzene and vinyl group that are left constitute styrene. The conjugation length is greater in stilbene than in the styrene. In a particle in a box picture the box is longer with stilbene and therefore the orbitals will be closer in energy. Beta carotene is a polyene with 11 double bonds, and it that makes orange juice the color orange. As molecules get longer the gap between the homo and lumo is smaller. So if you do something to a molecule that changes the conjugation length the absorption will change. The conjugation length requires orbitals and overlap. As you go from trans-stilbene to cis-stilbene you would expect a higher energy absorption. This system can undergo an electrocyclic ring closure resulting a dihydrophinanthrine. This molecule is not aromatic but it is 2 hydrogens away from being aromatic. A general rule is if a molecule is a step away from being aromatic the molecule will find a way to get there. This is an example of photochemical fatigue. The oxygen will pull out the two hydrogen. This is thermally reversible but once a molecule gets in the aromatic state the molecule tends to stay there.

Another classic example is azobenzene which also undergoes cis-trans isomerization. The cis form is not thermally stable and it reverts to the trans form. Cis stilbene are more stable than cis azobenzenes.

• The cis form is not thermally stable with respect to the trans form, so the cis form reverts back to the trans form in the dark.

• cis-stilbenes are more stable than their azobenzenes counterparts.

• The photochromic quantum yield is temperature dependent for both trans-stilbene, trans-azobenzene.

Heterocyclic Cleavage

Spiropyran and Spirooxazine have dramatic photochromic shifts but poor reversability

Merocyanines and spiropyrans have a heterolytic bond cleavage, the oxygen takes two electrons, the nitrogen gives up an electron and the electron does a cis-trans isomerization.

These molecules are characterized by relatively poor photochromic properties:

• low conversion quantum yields

• fast thermal back reaction

These molecules are used for various photochromic reactions but they break down after 10 ^5 repetitions. Their change in optical properties are dramatic and can be used for low repetition application such as real time holography in which an image is written but only needs to be changed a few times.

References

Previous Topic

Return to Absorption and Emission Menu

Next Topic