Difference between revisions of "Electronic Structure of Hydrogen"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| Line 13: | Line 13: | ||
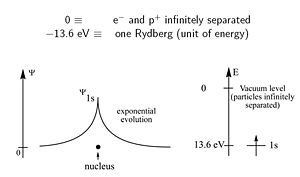
The hydrogen atom has just a electron and a proton. When you bring them together the atom holds together because of the coulombic attraction between the electron and the nucleus. That attraction leads to stabilization of the system of -13.6 ev (one Rydberg). This is how much energy it take to separate the proton from the electron. This does not happen at room temperature. The electron has a 1s atomic orbital. The wavefunction decreases as you move away from the nucleus. The square of the wavefunction gives the probability of finding an electron. It will not actually touch the nucleus but it will stay very close. | The hydrogen atom has just a electron and a proton. When you bring them together the atom holds together because of the coulombic attraction between the electron and the nucleus. That attraction leads to stabilization of the system of -13.6 ev (one Rydberg). This is how much energy it take to separate the proton from the electron. This does not happen at room temperature. The electron has a 1s atomic orbital. The wavefunction decreases as you move away from the nucleus. The square of the wavefunction gives the probability of finding an electron. It will not actually touch the nucleus but it will stay very close. | ||
When two hydrogen atoms approach one another: their ψ1s wavefunctions start overlapping and the 1s electrons start interacting. Molecular orbitals can be described using the atomic orbitals of the atoms forming the molecule. The hydrogen atom is the only element for which you can exactly solve | When two hydrogen atoms approach one another: their ψ1s wavefunctions start overlapping and the 1s electrons start interacting. Molecular orbitals can be described using the atomic orbitals of the atoms forming the molecule. The hydrogen atom is the only element for which you can exactly solve Schrodingers equation. Even Helium can not be solved exactly. Hydrogen molecule can be described using Linear Combination of Atomic Orbitals: LCAO. For n atomic orbitals you get n molecular orbitals. | ||
<br clear='all'> | <br clear='all'> | ||
=== Adding wavefunctions === | === Adding wavefunctions === | ||
Revision as of 12:15, 2 June 2009
| Previous Topic | Return to Band Structure Menu | Next Topic |
Electronc structure of hydrogen
The hydrogen atom has just a electron and a proton. When you bring them together the atom holds together because of the coulombic attraction between the electron and the nucleus. That attraction leads to stabilization of the system of -13.6 ev (one Rydberg). This is how much energy it take to separate the proton from the electron. This does not happen at room temperature. The electron has a 1s atomic orbital. The wavefunction decreases as you move away from the nucleus. The square of the wavefunction gives the probability of finding an electron. It will not actually touch the nucleus but it will stay very close.
When two hydrogen atoms approach one another: their ψ1s wavefunctions start overlapping and the 1s electrons start interacting. Molecular orbitals can be described using the atomic orbitals of the atoms forming the molecule. The hydrogen atom is the only element for which you can exactly solve Schrodingers equation. Even Helium can not be solved exactly. Hydrogen molecule can be described using Linear Combination of Atomic Orbitals: LCAO. For n atomic orbitals you get n molecular orbitals.
Adding wavefunctions
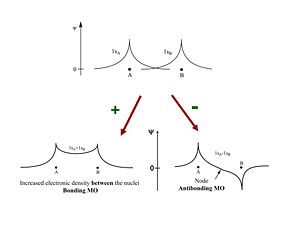
The two wave functions 1SA and 1SB can be added constructively to produce a bonding orbital, or with opposite sign they add destructively to produce an antibonding molecular orbital. This describes the system quite well. The bonding orbital will have lower energy and create a more stable system. There has to be an increased density of electrons between the nuclei in order to form a molecule. The node in the antibonding MO decreases the density electrons and decreases the stability required to bring the two protons together.
Bonding and antibonding
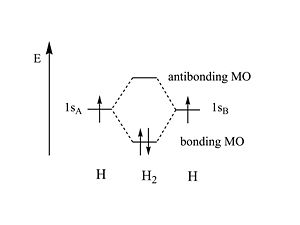
The energy of the bonding MO is lower than the energy of the two original atomic orbitals . If two electrons share the same wavefunction they have to opposite spins. When 2 hydrogen atoms form from electrons and protons the energy is 27.4 eV. The energy of the hydrogen bond 4eV; far smaller than the atomic bond energy.
| Previous Topic | Return to Band Structure Menu | Next Topic |