Difference between revisions of "Atomic Orbitals and Nodes"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| Line 37: | Line 37: | ||
|- | |- | ||
! Li | ! Li | ||
| 1s<sup>2</sup> || 2s<sup>1</sup> || | | 1s<sup>2</sup> || 2s<sup>1</sup> || | ||
|- | |- | ||
! Be | ! Be | ||
| 1s<sup>2</sup> || 2s<sup>2</sup> || | | 1s<sup>2</sup> || 2s<sup>2</sup> || | ||
|- | |- | ||
! B | ! B | ||
| 1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>1</sup> | | 1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>1</sup> | ||
|- | |- | ||
! C | ! C | ||
| 1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>2</sup> | | 1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>2</sup> | ||
|- | |- | ||
! N | ! N | ||
| 1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>3</sup> | | 1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>3</sup> | ||
|- | |- | ||
! O | ! O | ||
|1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>4</sup> | |1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>4</sup> | ||
|- | |- | ||
! F | ! F | ||
|1s<sup>2</sup>|| 2s<sup>2</sup> || 2p<sup>5</sup> | |1s<sup>2</sup>|| 2s<sup>2</sup> || 2p<sup>5</sup> | ||
|- | |- | ||
! Ne | ! Ne | ||
|1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>6</sup> | |1s<sup>2</sup> || 2s<sup>2</sup> || 2p<sup>6</sup> | ||
|} | |} | ||
Revision as of 11:40, 18 May 2009
Return to Molecular Obrbitals Menu | Next Topic
Atomic Orbitals
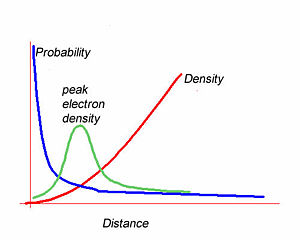
Orbitals are important becuase they determine the distribution of electrons in molecules, which in turn determines the electronic and optical properties of materials. Atomic orbitals are wave functions that are solutions to the Schrödinger equation. This equation allows us to figure out the wave functions and associated energies in atomic orbitals. The square of the wave function gives the probability of finding an electron at a certain point. The integral of the wavefunction over a voluem gives the enclosed electron density within that volume. The most likely position to find the 1s electron is at the nucleus.However the most likely radius is at some distance from the nucleus. The graph of wavefunction vs distance falls off exponentially as you move away from the nucleus. The electron density builds quadratically with distance from the nuclues. The peak electron density will be the product of the these two functions. This results in a curve with a density peak at a certain distance. Wavefunctions alone do not tell you the electron density.
The p orbitals have orientations along the x, y and z axes. A node is a place where there is zero probability of finding an electron. A radial node has a sperical surface with zero probability. P orbitals have an angular node along axes. We usually indicate the sign of the wave function in drawings by shading the orbital as black and white, or blue and green.
1s: no node 2s: one radial node, 2p one angular node 3s: two radial nodes, 3p one radial node one angular node, 3d two angular nodes
The more nodes the higher the energy of the orbitals. The more the function varies spatially, the higher the energy.
Core and valence electrons
Core electrons are very tightly bound tot he nucleus and spend most of their time very close to the nucleus. They are largely unaffected by the presence of nearby atoms.
Valence electrons are less tightly bound to the nucleus and are in the outermost "shell". These electrons are easily affected by the presence of other atoms and the ones that are critical for bonding between atoms.
According to the Aufbau principle we start adding electrons to the 2s orbital and then to the three 2p orbitals, each of which can have up to two electrons. The orbitals are filled from lowest energy to the highest. Here are the electron configuration for row two of the periodic table. The 1s orbitals are core while the two 2s and 2p orbitals are valence electrons. Neon has a full octet so it is non-reactive, ie a noble gas.
| <math>element</math> | <math>1s</math> | <math>2s</math> | <math>2p</math> | |
|---|---|---|---|---|
| Li | 1s2 | 2s1 | ||
| Be | 1s2 | 2s2 | ||
| B | 1s2 | 2s2 | 2p1 | |
| C | 1s2 | 2s2 | 2p2 | |
| N | 1s2 | 2s2 | 2p3 | |
| O | 1s2 | 2s2 | 2p4 | |
| F | 1s2 | 2s2 | 2p5 | |
| Ne | 1s2 | 2s2 | 2p6 |
Here is the general rules for filling orbitals.
| <math>s</math> | <math>p</math> | <math>d</math> | <math>f</math> | <math>g</math> | |
|---|---|---|---|---|---|
| 1 | 1 | ||||
| 2 | 2 | 3 | |||
| 3 | 4 | 5 | 7 | ||
| 4 | 6 | 8 | 10 | 13 | |
| 5 | 9 | 11 | 14 | 17 | 21 |
| 6 | 12 | 15 | 18 | 22 | 26 |
| 7 | 16 | 19 | 23 | 27 | 31 |
| 8 | 20 | 24 | 28 | 32 | 36 |